Calculus AB and Calculus BC
CHAPTER 4 Applications of Differential Calculus
M. RELATED RATES
If several variables that are functions of time t are related by an equation, we can obtain a relation involving their (time) rates of change by differentiating with respect to t.
EXAMPLE 36
If one leg AB of a right triangle increases at the rate of 2 inches per second, while the other leg AC decreases at 3 inches per second, find how fast the hypotenuse is changing when AB = 6 feet and AC = 8 feet.
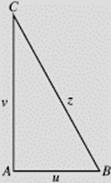
FIGURE N4–21
SOLUTION: See Figure N4–21. Let u, v, and z denote the lengths respectively of AB, AC, and BC. We know that 
Since (at any time) z2 = u2 + v2, then
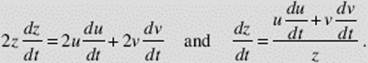
At the instant in question, u = 6, v = 8, and z = 10, so
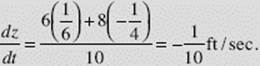
EXAMPLE 37
The diameter and height of a paper cup in the shape of a cone are both 4 inches, and water is leaking out at the rate of 
cubic inch per second. Find the rate at which the water level is dropping when the diameter of the surface is 2 inches.
SOLUTION: See Figure N4–22. We know that 
and that h = 2r.
Here, 
at any time.
When the diameter is 2 in., so is the height, and 
The water level is thus dropping at the rate of 
in./sec.
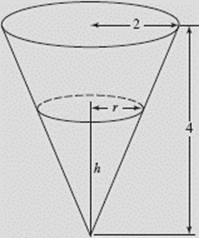
FIGURE N4–22
EXAMPLE 38
Suppose liquid is flowing into a vessel at a constant rate. The vessel has the shape of a hemisphere capped by a cylinder, as shown in Figure N4–23. Graph y = h(t), the height (= depth) of the liquid at time t, labeling and explaining any salient characteristics of the graph.
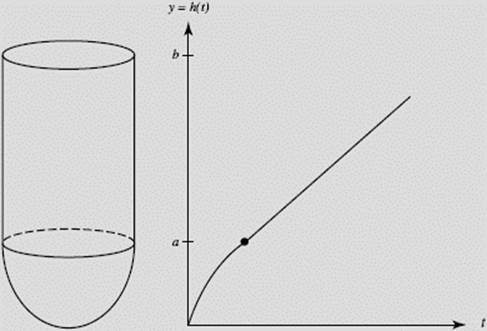
FIGURE N4–23
SOLUTION: Liquid flowing in at a constant rate means the change in volume is constant per unit of time. Obviously, the depth of the liquid increases as t does, so h ′(t) is positive throughout. To maintain the constant increase in volume per unit of time, when the radius grows, h ′(t) must decrease. Thus, the rate of increase of h decreases as h increases from 0 to a (where the cross-sectional area of the vessel is largest). Therefore, since h ′(t) decreases, h ″(t) < 0 from 0 to a and the curve is concave down.
As h increases from a to b, the radius of the vessel (here cylindrical) remains constant, as do the cross-sectional areas. Therefore h ′(t) is also constant, implying that h(t) is linear from a to b.
Note that the inflection point at depth a does not exist, since h ″(t) < 0 for all values less than a but is equal to 0 for all depths greater than or equal to a.
BC ONLY