Calculus AB and Calculus BC

CHAPTER 4 Applications of Differential Calculus

N. SLOPE OF A POLAR CURVE

We know that, if a smooth curve is given by the parametric equations

x = f (t) and y = g(t),

then

provided that f ′(t) ≠ 0.

To find the slope of a polar curve r = f (θ), we must first express the curve in parametric form. Since

x = r cos θ and y = r sin θ,

therefore,

x = f (θ) cos θ and y = f (θ) sin θ.

If f (θ) is differentiable, so are x and y; then

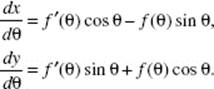
Also, if then

In doing an exercise, it is often easier simply to express the polar equation parametrically, then find dy/dx, rather than to memorize the formula.

EXAMPLE 39

(a) Find the slope of the cardioid r = 2(1 + cos θ) at See Figure N4–24.

(b) Where is the tangent to the curve horizontal?

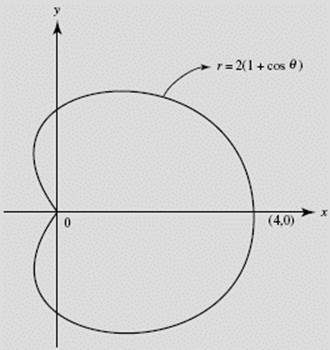
FIGURE N4–24

BC ONLY

SOLUTIONS:

(a) Use r = 2(1 + cos θ), x = r cos θ, y = r sin θ, and r ′ = −2 sin θ; then

At

(b) Since the cardioid is symmetric to θ = 0 we need consider only the upper half of the curve for part (b). The tangent is horizontal where (provided ). Since factors into 2(2 cos θ − 1)(cos θ + 1), which equals 0 for cos or −1, or π. From part (a), does equal 0 at π. Therefore, the tangent is horizontal only at (and, by symmetry, at ).

It is obvious from Figure N4–24 that r ′(θ) does not give the slope of the cardioid. As θ varies from 0 to the slope varies from −∞ to 0 to +∞ (with the tangent rotating counterclockwise), taking on every real value. However, r ′(θ) equals −2 sin θ, which takes on values only between −2 and 2!

Chapter Summary

In this chapter we reviewed many applications of derivatives. We’ve seen how to find slopes of curves and used that skill to write equations of lines tangent to a curve. Those lines often provide very good approximations for values of functions. We have looked at ways derivatives can help us understand the behavior of a function. The first derivative can tell us whether a function is increasing or decreasing and locate maximum and minimum points. The second derivative can tell us whether the graph of the function is concave upward or concave downward and locate points of inflection. We’ve reviewed how to use derivatives to determine the velocity and acceleration of an object in motion along a line and to describe relationships among rates of change.

For BC Calculus students, this chapter reviewed finding slopes of curves defined parametrically or in polar form. We have also reviewed the use of vectors to describe the position, velocity, and acceleration of objects in motion along curves.