Calculus AB and Calculus BC

CHAPTER 5 Antidifferentiation

D. INTEGRATION BY PARTS

Parts Formula

The Parts Formula stems from the equation for the derivative of a product:

or, or more conveniently d(uv) = u dv + v du.

Hence, u dv = d(uv) − v du and integrating gives us or

the Parts Formula. Success in using this important technique depends on being able to separate a given integral into parts u and dv so that (a) dv can be integrated, and (b) du is no more difficult to calculate than the original integral.

EXAMPLE 43

Find

SOLUTION: We let u = x and dv = cos x dx. Then du = dx and v = sin x. Thus, the Parts Formula yields

EXAMPLE 44

Find

SOLUTION: We let u = x² and dv = e^x dx. Then du = 2x dx and v = e^x, so We use the Parts Formula again, this time letting u = x and dv = e^x dx so that du = dx and v = e^x. Thus,

EXAMPLE 45

Find I =

SOLUTION: To integrate, we can let u = e^x and dv = cos x dx; then du = e^x dx, v = sin x. Thus,

To evaluate the integral on the right, again we let u = e^x, dv = sin x dx, so that du = e^x dx and v = − cos x. Then,

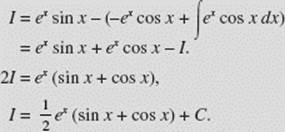
EXAMPLE 46

Find

SOLUTION: We let u = ln x and dv = x⁴ dx. Then, and Thus,

THE TIC-TAC-TOE METHOD. ¹

This method of integrating is extremely useful when repeated integration by parts is necessary. To integrate we construct a table as follows:

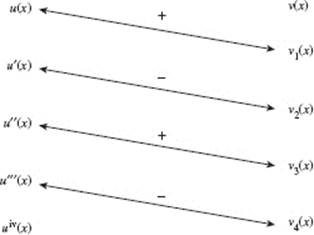
Here the column at the left contains the successive derivatives of u(x). The column at the right contains the successive antiderivatives of v(x) (always with C = 0); that is, v₁ (x) is the antiderivative of v(x), v₂ (x) is the antiderivative of v₁ (x), and so on. The diagonal arrows join the pairs of factors whose products form the successive terms of the desired integral; above each arrow is the sign of that term. By the tic-tac-toe method,

EXAMPLE 47

To integrate cos x dx by the tic-tac-toe method, we let u(x) = x⁴ and v(x) = cos x, and get the following table:

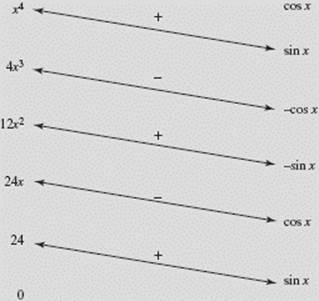
The method yields

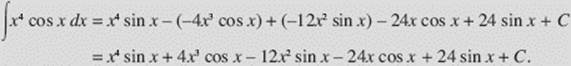
With the ordinary method we would have had to apply the Parts Formula four times to perform this integration.

¹ This method was described by K. W. Folley in Vol. 54 (1947) of the American Mathematical Monthly and was referred to in the movie Stand and Deliver.