Calculus AB and Calculus BC

CHAPTER 6 Definite Integrals

B. PROPERTIES OF DEFINITE INTEGRALS

The following theorems about definite integrals are important.

Fundamental Theorem of calculus

The evaluation of a definite integral is illustrated in the following examples. A calculator will be helpful for some numerical calculations.

EXAMPLE 1

EXAMPLE 2

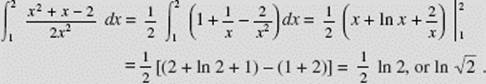
EXAMPLE 3

EXAMPLE 4

EXAMPLE 5

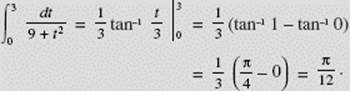
EXAMPLE 6

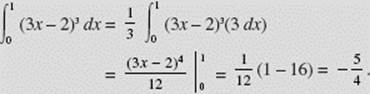
EXAMPLE 7

EXAMPLE 8

BC ONLY

EXAMPLE 9

EXAMPLE 10

BC ONLY

EXAMPLE 11

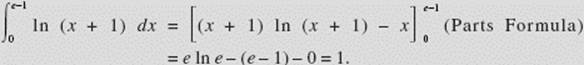
BC ONLY

EXAMPLE 12

SOLUTION: We use the method of partial fractions and set

Solving for A and B yields Thus,

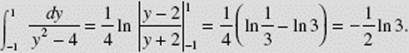
EXAMPLE 13

EXAMPLE 14

EXAMPLE 15

EXAMPLE 16

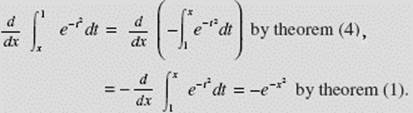
EXAMPLE 17

Given find F ′(x).

SOLUTION:

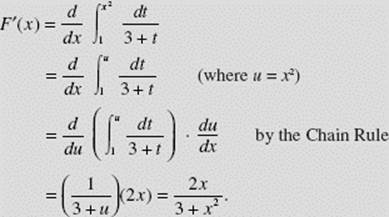
EXAMPLE 18

If find F ′(x).

SOLUTION: We let u = cos x. Thus

EXAMPLE 19

Find

SOLUTION:

Here we have let and noted that

where

The limit on the right in the starred equation is, by definition, the derivative of F(x), that is, f (x).

EXAMPLE 20

Reexpress in terms of u if

SOLUTION: When u² = x − 2, and 2u du = dx. The limits of the given integral are values of x. When we write the new integral in terms of the variable u, then the limits, if written, must be the values of u that correspond to the given limits. Thus, when x = 3, u = 1, and whenx = 6, u = 2. Then

EXAMPLE 21

If g ′ is continuous, find

SOLUTION:

Note that the expanded limit is, by definition, the derivative of g(x) at c.