Calculus AB and Calculus BC
CHAPTER 6 Definite Integrals
F. INTERPRETING ln x AS AN AREA
It is quite common to define ln x, the natural logarithm of x, as a definite integral, as follows:
![]()
This integral can be interpreted as the area bounded above by the curve ![]() below by the t-axis, at the left by t = 1, and at the right by t = x (x > 1). See Figure N6–16.
below by the t-axis, at the left by t = 1, and at the right by t = x (x > 1). See Figure N6–16.
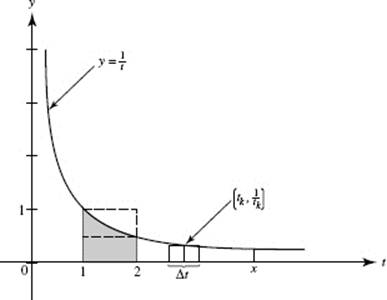
FIGURE N6–16
Note that if x = 1 the above definition yields ln 1 = 0, and if 0 < x < 1 we can rewrite as follows:
![]()
showing that ln x < 0 if 0 < x < 1.
With this definition of ln x we can approximate ln x using rectangles or trapezoids.
EXAMPLE 35
Show that ![]() < ln 2 < 1.
< ln 2 < 1.
SOLUTION: Using the definition of ln x above yields ![]() which we interpret as the area under
which we interpret as the area under ![]() above the t-axis, and bouned at the left by t = 1 and at the right by t = 2 (the shaded region in Figure N6–16). Since
above the t-axis, and bouned at the left by t = 1 and at the right by t = 2 (the shaded region in Figure N6–16). Since ![]() is strictly decreasing, the area of the inscribed rectangle (height
is strictly decreasing, the area of the inscribed rectangle (height ![]() width 1) is less than ln 2, which, in turn, is less than the area of the circumscribed rectangle (height 1, width 1). Thus
width 1) is less than ln 2, which, in turn, is less than the area of the circumscribed rectangle (height 1, width 1). Thus
![]()
EXAMPLE 36
Find L(5), R(5), and T(5) for ![]()
SOLUTION: Noting that for n = 5 subintervals on the interval [1,6] we have Δx = 1, we make a table of values for ![]()
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
|
f (x) |
120 |
60 |
40 |
30 |
24 |
20 |
Then:
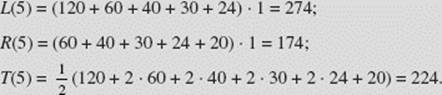
NOTE: The calculator finds that ![]() is approximately 215.011.
is approximately 215.011.