Calculus AB and Calculus BC
CHAPTER 6 Definite Integrals
Practice Exercises
Part A. Directions: Answer these questions without using your calculator.
1. 
(A) 
(B) 0
(C) 
(D) −2
(E) −1
2. 
(A) 
(B) 
(C) 1 − ln 2
(D) 
(E) 1
3. 
(A) 1
(B) −2
(C) 4
(D) −1
(E) 2
4. 
(A) 2
(B) 
(C) 
(D) 6
(E) 
5. 
(A) ln 3
(B) 
(C) 
(D) ln 
(E) 
6. 
(A) 1
(B) 
(C) 
(D) −1
(E) 2
7. 
(A) 
(B) 6
(C) 
(D) 0
(E) 4
8. 
(A) 
(B) 
(C) 
(D) 
(E) 
9. 
(A) 
(B) 0
(C) 
(D) 
(E) 
10. 
(A) 
(B) 1 − e
(C) 
(D) 
(E) 
11. 
(A) e − 1
(B) 
(C) 2(e − 1)
(D) 
(E) 
12. 
(A) 2
(B) 
(C) −1
(D) 
(E) −2
13. 
(A) −ln 2
(B) 
(C) 
(D) 
(E) ln 2
14. If we let x = 2 sin θ, then 
is equivalent to
(A) 
(B) 
(C) 
(D) 
(E) none of these
15. 
(A) 
(B) 
(C) 1
(D)
(E) 0
16. 
(A) 
(B) 
(C) 0
(D) 1
(E) e − 1
17. 
(A) −1
(B) e + 1
(C) 1
(D) e − 1
(E) 
BC ONLY
18. 
(A) ln 2
(B) 
(C) 
(D) 
(E) 
19. 
(A) 
(B) 
(C) 
(D) ln 3
(E) 
20. 
(A) 
(B) 
(C) 
(D) −1
(E) 
21. 
(A) 
(B) 1
(C)
(D) 
(E) −1
22. 
(A) e
(B) 2 + e
(C) 
(D) 1 + e
(E) e − 1
23. 
(A) ln 2
(B) e
(C) 1 + e
(D) −ln 2
(E) 
24. If we let x = tan θ, then 
is equivalent to
(A) 
(B) 
(C) 
(D) 
(E) 
25. If the substitution 
is used, then 
is equivalent to
(A) 
(B) 
(C) 
(D) 
(E) 
26. The table above shows some values of continuous function f and its first derivative. Evaluate 
|
x |
f (x) |
f ′(x) |
|
0 |
11 |
3 |
|
2 |
15 |
2 |
|
4 |
16 |
−1 |
|
6 |
12 |
−3 |
|
8 |
7 |
0 |
(A) −1/2
(B) −3/8
(C) 3
(D) 4
(E) none of these
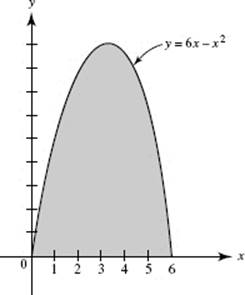
27. Using M(3), we find that the approximate area of the shaded region below is
(A) 9
(B) 19
(C) 36
(D) 38
(E) 54
28. The graph of a continuous function f passes through the points (4,2), (6,6), (7,5), and (10,8). Using trapezoids, we estimate that 
(A) 25
(B) 30
(C) 32
(D) 33
(E) 41
29. The area of the shaded region in the figure is equal exactly to ln 3. If we approximate ln 3 using L(2) and R(2), which inequality follows?
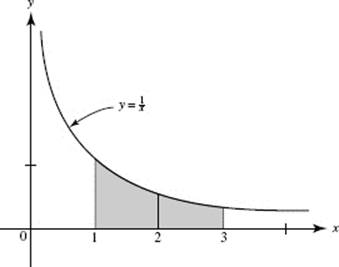
(A) 
(B) 
(C) 
(D) 
(E) 
30. Let 
We estimate A using the L, R, and T approximations with n = 100 subintervals. Which is true?
(A) L < A < T < R
(B) L < T < A < R
(C) R < A < T < L
(D) R < T < A < L
(E) The order cannot be determined.
31. 
(A)
(B) 4
(C) 
(D) 5
(E) 
32. 
(A) 
(B)
(C) 5
(D) 
(E) 
33. The average value of 
on its domain is
(A) 2
(B) 4
(C) 2π
(D) 4π
(E) none of these
34. The average value of cos x over the interval 
(A) 
(B) 
(C) 
(D) 
(E) 
35. The average value of csc2 x over the interval from 
(A) 
(B) 
(C) 
(D) 
(E) 
Part B. Directions: Some of the following questions require the use of a graphing calculator.
36. Find the average value of function f, as shown in the graph below, on the interval [0,5].
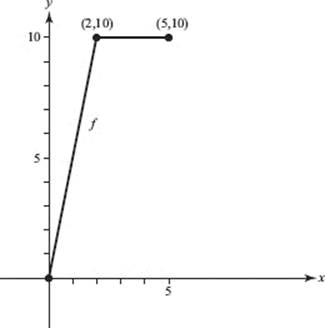
(A) 2
(B) 4
(C) 5
(D) 7
(E) 8
37. The integral 
gives the area of
(A) a circle of radius 4
(B) a semicircle of radius 4
(C) a quadrant of a circle of radius 4
(D) an ellipse whose semimajor axis is 4
(E) none of these
38. 
(A) 0.25
(B) 0.414
(C) 1.000
(D) 1.414
(E) 2.000
Use the graph of function f, shown below, for questions 39–42.
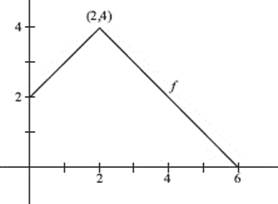
39. In which of these intervals is there a value c for which f (c) is the average value of f over the interval [0,6]?
I. [0,2]
II. [2,4]
III. [4,6]
(A) I only
(B) II only
(C) III only
(D) I and II only
(E) none of these, because f is not differentiable on [0,6]
40. 
(A) −2
(B) 
(C) 0
(D) 
(E) 2
41. Let g(x) = 
then g ′(1)
(A) = 3.
(B) = 4.
(C) = 6.
(D) = 8.
(E) does not exist, because f is not differentiable at x = 2.
42. Let h(x) = x2 − f (x). Find 
(A) 22
(B) 38
(C) 58
(D) 70
(E) 74
43. If f (x) is continuous on the closed interval [a,b], then there exists at least one number c, a < c < b, such that 
is equal to
(A) 
(B) f ′(c)(b − a)
(C) f (c)(b − a)
(D) 
(E) f (c)[f (b) − f (a)]
44. If f (x) is continuous on the closed interval [a,b] and k is a constant, then 
is equal to
(A) k(b − a)
(B) k[f (b) − f (a)]
(C) kF(b − a), where 
(D) 
(E) 
45. 
(A) 
(B) 
(C) 
(D) 
(E) none of these
46. If 
then F ′(u) is equal to
(A) −6u(2 − u2)2
(B) 
(C) (2 − u2)3 − 1
(D) (2 − u2)3
(E) −2u(2 − u2)3
47. 
(A) 
(B) 
(C) 
(D) 
(E) 
48. If x = 4 cos θ and y = 3 sin θ, then 
is equivalent to
(A) 
(B) 
(C) 
(D) 
(E) 
49. A curve is defined by the parametric equations x = 2a tan θ and y = 2a cos2 θ, where 0 
θ π. Then the definite integral 
is equivalent to
(A) 
(B) 
(C) 
(D) 
(E) 
BC ONLY
50. A curve is given parametrically by x = 1 − cos t and y = t − sin t, where 0 
t π. Then 
is equivalent to
(A) 
(B) 
(C) 
(D) 
(E) 
BC ONLY
51. When 
is estimated using n = 5 subintervals of equal width, which is (are) true?
I. 
II. 
III. 
(A) II only
(B) III only
(C) I and II only
(D) I and III only
(E) II and III only
52. Find the value of x at which the function y = x2 reaches its average value on the interval [0,10].
(A) 4.642
(B) 5
(C) 5.313
(D) 5.774
(E) 7.071
53. The average value of 
on the interval 0 ≤ x ≤ 5 is
(A) 8
(B) 9.2
(C) 16
(D) 23
(E) undefined because f is not differentiable on this interval