Calculus AB and Calculus BC

CHAPTER 8 Further Applications of Integration

B. MOTION ALONG A PLANE CURVE

BC ONLY

In Chapter 4, §K, it was pointed out that, if the motion of a particle P along a curve is given parametrically by the equations x = x(t) and y = y(t), then at time t the position vector R, the velocity vector v, and the acceleration vector a are:

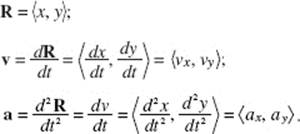
The components in the horizontal and vertical directions of R, v, and a are given respectively by the coefficients of i and j in the corresponding vector. The slope of v is its magnitude,

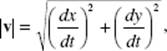
is the speed of the particle, and the velocity vector is tangent to the path. The slope of a is The distance the particle travels from time t₁ to t₂, is given by

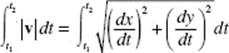
How integration may be used to solve problems of curvilinear motion is illustrated in the following examples.

BC ONLY

EXAMPLE 4

Suppose a projectile is launched from the origin at an angle of elevation α and initial velocity v₀. Find the parametric equations for its flight path.

SOLUTION: We have the following initial conditions:

Position: x(0) = 0; y(0) = 0.

Velocity:

We start with equations representing acceleration due to gravity and integrate each twice, determining the constants as shown:

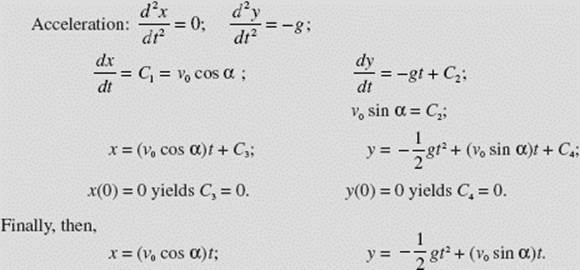
If desired, t can be eliminated from this pair of equations to yield a parabola in rectangular coordinates.

EXAMPLE 5

A particle P(x, y) moves along a curve so that

at any time t 0.

At t = 0, x = 1 and y = 0. Find the parametric equations of motion.

SOLUTION: Since we integrate to get and use

x(0) = 1 to find that C = 2. Therefore, and

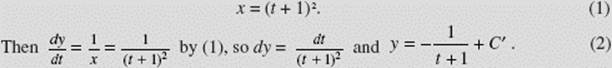
Since y(0) = 0, this yields C ′ = 1, and so (2) becomes

Thus the parametric equations are

BC ONLY

EXAMPLE 6

The particle in Example 5 is in motion for 1 second, 0 ≤ t ≤ 1. Find its position, velocity, speed, and acceleration at t = 1 and the distance it traveled.

SOLUTION: In Example 5 we derived the result the parametric representation of the particle’s position. Hence its position at t = 1 is

From P(t) we write the velocity vector:

Hence, at t = 1 the particle’s velocity is

Speed is the magnitude of the velocity vector, so after 1 second the particle’s speed is

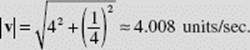
The particle’s acceleration vector at t = 1 is

On the interval 0 ≤ t ≤ 1 the distance traveled by the particle is

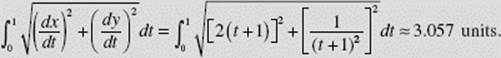
BC ONLY

EXAMPLE 7

A particle P(x, y) moves along a curve so that its acceleration is given by

when t = 0, the particle is at (1, 0) with

(a) Find the position vector R at any time t.

(b) Find a Cartesian equation for the path of the particle, and identify the conic on which P moves.

SOLUTIONS:

(a) and since when t = 0, it follows that c₁ = c₂ = 0. So Also and since when t = 0, we see that c₃ = c₄ = 0. Finally, then,

(b) From (a) the parametric equations of motion are

x = cos 2t, y = 2 sin t.

By a trigonometric identity,

P travels in a counterclockwise direction along part of a parabola that has its vertex at (1, 0) and opens to the left. The path of the particle is sketched in Figure N8–1; note that −1 ≤ x ≤ 1, −2 ≤ y ≤ 2.

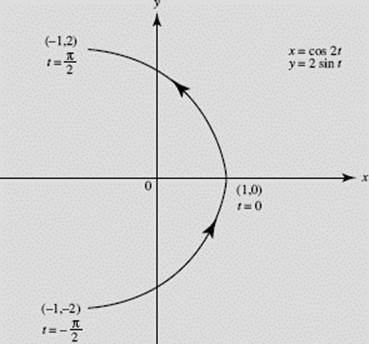
FIGURE N8–1