Calculus AB and Calculus BC

CHAPTER 9 Differential Equations

D. SOLVING FIRST-ORDER DIFFERENTIAL EQUATIONS ANALYTICALLY

In the preceding sections we solved differential equations graphically, using slope fields, and numerically, using Euler’s method. Both methods yield approximations. In this section we review how to solve some differential equations exactly.

Separating Variables

A first-order d.e. in x and y is separable if it can be written so that all the terms involving y are on one side and all the terms involving x are on the other.

A differential equation has variables separable if it is of the form

The general solution is

EXAMPLE 8

Solve the d.e. given the initial condition y(0) = 2.

SOLUTION: We rewrite the equation as y dy = −x dx. We then integrate, getting

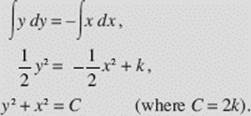
Since y(0) = 2, we get 4 + 0 = C; the particular solution is therefore x² + y² = 4. (We need to specify above that y > 0. Why?)

EXAMPLE 9

If and t = 0 when s = 1, find s when t = 9.

SOLUTION: We separate variables:

then integration yields

Using s = 1 and t = 0, we get so C = + 2. Then

When t = 9, we find that s^1/2 = 9 + 1, so s = 100.

EXAMPLE 10

If (ln y) and y = e when x = 1, find the value of y greater than 1 that corresponds to x = e⁴.

SOLUTION: Separating, we get We integrate:

Using y = e when x = 1 yields so

When x = e⁴, we have thus ln² y = 9 and ln y = 3 (where we chose ln y > 0 because y > 1), so y = e³.

EXAMPLE 11

Find the general solution of the differential equation

SOLUTION: We rewrite

Taking antiderivatives yields e^u = e^v + C, or u = ln(e^v + c).