Calculus AB and Calculus BC

CHAPTER 10 Sequences and Series

B. INFINITE SERIES

B1. Definitions.

Infinite series

If a_n is a sequence of real numbers, then an infinite series is an expression of the form

The elements in the sum are called terms; a_n is the nth or general term of the series.

EXAMPLE 7

A series of the form is called a p-series.

The p-series for p = 2 is

EXAMPLE 8

The p-series with p = 1 is called the harmonic series:

EXAMPLE 9

A geometric series has a first term, a, and common ratio of terms, r:

If there is a finite number S such that

then we say that infinite series is convergent, or converges to S, or has the sum S, and we write, in this case,

When there is no source of confusion, the infinite series (1) may be indicated simply by

EXAMPLE 10

Show that the geometric series converges to 2.

SOLUTION: Let S represent the sum of the series; then:

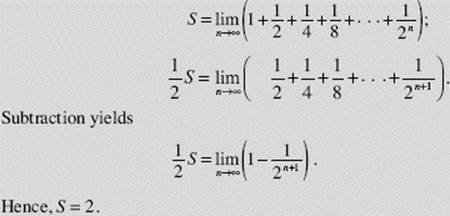
EXAMPLE 11

Show that the harmonic series diverges.

SOLUTION The terms in the series can be grouped as follows:

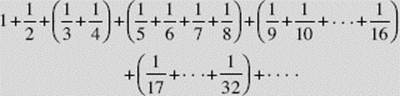
This sum clearly exceeds

which equals

Since that sum is not bounded, it follows that diverges to ∞.

B2. Theorems About Convergence or Divergence of Infinite Series.

The following theorems are important.

THEOREM 2a. If converges, then

This provides a convenient and useful test for divergence, since it is equivalent to the statement: If a_n does not approach zero, then the series diverges. Note, however, particularly that the converse of Theorem 2a is not true. The condition that a_n approach zero is necessary but not sufficient for the convergence of the series. The harmonic series is an excellent example of a series whose nth term goes to zero but that diverges (see Example 11 above). The series diverges because not zero; the series does not converge (as will be shown shortly) even though

THEOREM 2b. A finite number of terms may be added to or deleted from a series without affecting its convergence or divergence; thus

(where m is any positive integer) both converge or both diverge. (Note that the sums most likely will differ.)

THEOREM 2c. The terms of a series may be multiplied by a nonzero constant without affecting the convergence or divergence; thus

both converge or both diverge. (Again, the sums will usually differ.)

THEOREM 2d. If both converge, so does

THEOREM 2e. If the terms of a convergent series are regrouped, the new series converges.

B3. Tests for Convergence of Infinite Series.

THE nth TERM TEST

If diverges.

NOTE: When working with series, it’s a good idea to start by checking the nth Term Test. If the terms don’t approach 0, the series cannot converge. This is often the quickest and easiest way to identify a divergent series.

(Because this is the contrapositive of Theorem 2a, it’s always true. But beware of the converse! Seeing that the terms do approach 0 does not guarantee that the series must converge. It just means that you need to try other tests.)

EXAMPLE 12

Does converge or diverge?

SOLUTION: Since the series diverges by the nth Term Test.

THE GEOMETRIC SERIES TEST

A geometric series converges if and only if |r| < 1.

If |r| < 1, the sum is

The series cannot converge unless it passes the nth Term Test; only if |r| < 1. As noted earlier, this is a necessary condition for convergence, but may not be sufficient. We now examine the sum using the same technique we employed in Example 10:

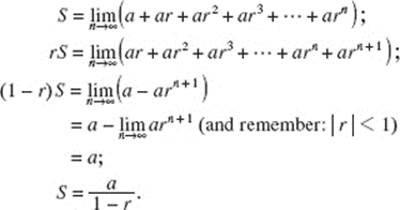
EXAMPLE 13

Does 0.3 + 0.03 + 0.003 + · · · converge or diverge?

SOLUTION: The series 0.3 + 0.03 + 0.003 + · · · is geometric with a = 0.3 and r = 0.1. Since |r| < 1, the series converges, and its sum is

NOTE: = 0.333 …, which is the given series.

B4. Tests for Convergence of Nonnegative Series.

The series is called a nonnegative series if a_n ≥ 0 for all n.

THE INTEGRAL TEST

If f (x) is a continuous, positive, decreasing function and f (n) = a_n, then converges if and only if the improper integral converges.

EXAMPLE 14

Does converge?

SOLUTION: The associated improper integral is

which equals

The improper integral and the infinite series both diverge.

EXAMPLE 15

Test the series for convergence.

SOLUTION: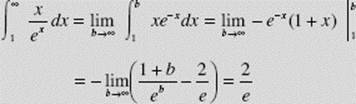

by an application of L’Hôpital’s Rule. Thus converges.

THE p-SERIES TEST

A p-series converges if p > 1, but diverges if p ≤ 1.

This follows immediately from the Integral Test and the behavior of improper integrals of the form

EXAMPLE 16

Does the series converge or diverge?

SOLUTION: The series is a p-series with p = 3;

hence the series converges by the p-Series Test.

EXAMPLE 17

Does the series converge or diverge?

SOLUTION: diverges, because it is a p-series with

THE COMPARISON TEST

We compare the general term of the nonnegative series we are investigating, with the general term of a series known to converge or diverge.

(1) If converges and a_n u_n, then converges.

(2) If diverges and a_n u_n, then diverges.

Any known series can be used for comparison. Particularly useful are p-series, which converge if p > 1 but diverge if p 1, and geometric series, which converge if |r| < 1 but diverge if |r| 1.

EXAMPLE 18

Does converge or diverge?

SOLUTION: Since and the p-series converges, converges by the Comparison Test.

EXAMPLE 19

Does the series converge or diverge?

SOLUTION: diverges, since

the latter is the general term of the divergent p-series where and

Remember in using the Comparison Test that you may either discard a finite number of terms or multiply each term by a nonzero constant without affecting the convergence of the series you are testing.

EXAMPLE 20

Show that converges.

SOLUTION: For is a convergent geometric series with

THE LIMIT COMPARISON TEST

If is finite and nonzero, then and both converge or both diverge.

This test is useful when the direct comparisons required by the Comparison Test are difficult to establish. Note that, if the limit is zero or infinite, the test is inconclusive and some other approach must be used.

EXAMPLE 21

Does converge or diverge?

SOLUTION: This series seems to be related to the divergent harmonic series, but so the comparison fails. However, the Limit Comparison Test yields:

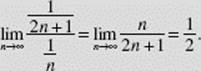
Since also diverges by the Limit Comparison Test.

THE RATIO TEST

Let if it exists. Then converges if L < 1 and diverges if L > 1.

If L = 1, this test is inconclusive; apply one of the other tests.

EXAMPLE 22

Does converge or diverge?

SOLUTION: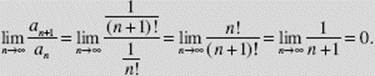

Therefore this series converges by the Ratio Test.

EXAMPLE 23

Does converge or diverge?

SOLUTION:

and

(See §E2.) Since e > 1, diverges by the Ratio Test.

EXAMPLE 24

If the Ratio Test is applied to any p-series, then

But if p > 1 then converges, while if p 1 then diverges. This illustrates the failure of the Ratio Test to resolve the question of convergence when the limit of the ratio is 1.

THE nth ROOT TEST

Let if it exists. Then converges if L < 1 and diverges if L > 1.

If L = 1 this test is inconclusive; try one of the other tests.

Note that the decision rule for this test is the same as that for the Ratio Test.

EXAMPLE 25

The series converges by the nth Root Test, since

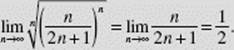
B5. Alternating Series and Absolute Convergence.

Any test that can be applied to a nonnegative series can be used for a series all of whose terms are negative. We consider here only one type of series with mixed signs, the so-called alternating series. This has the form:

where a_k > 0. The series

is the alternating harmonic series.

THE ALTERNATING SERIES TEST

An alternating series converges if:

(1) a_{n + 1} < a_n for all n, and

(2)

EXAMPLE 26

Does the series converge or diverge?

SOLUTION: The alternating harmonic series converges, since

(1) for all n and

(2)

EXAMPLE 27

Does the series converge or diverge?

SOLUTION: The series diverges, since we see that is 1, not 0. (By the nth Term Test, if a_n does not approach 0, then does not converge.)

DEFINITION

Absolute convergence

A series with mixed signs is said to converge absolutely (or to be absolutely convergent) if the series obtained by taking the absolute values of its terms converges; that is, converges absolutely if converges.

A series that converges but not absolutely is said to converge conditionally (or to be conditionally convergent). The alternating harmonic series converges conditionally since it converges, but does not converge absolutely. (The harmonic series diverges.)

When asked to determine whether an alternating series is absolutely convergent, conditionally convergent, or divergent, it is often advisable to first consider the series of absolute values. Check first for divergence, using the nth Term Test. If that test shows that the series may converge, investigate further, using the tests for nonnegative series. If you find that the series of absolute values converges, then the alternating series is absolutely convergent. If, however, you find that the series of absolute values diverges, then you’ll need to use the Alternating Series Test to see whether the series is conditionally convergent.

EXAMPLE 28

Determine whether converges absolutely, converges conditionally, or diverges.

SOLUTION: We see that not 0, so by the nth Term Test the series is divergent.

EXAMPLE 29

Determine whether 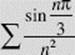converges absolutely, converges conditionally, or diverges.

SOLUTION: Note that, since 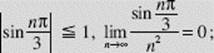the series passes the nth Term Test.

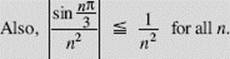
But is the general term of a convergent p-series (p = 2), so by the Comparison Test the nonnegative series converges, and therefore the alternating series converges absolutely.

EXAMPLE 30

Determine whether converges absolutely, converges conditionally, or diverges.

SOLUTION: is a p-series with so the nonnegative series diverges.

We see that

so the alternating series converges; hence is conditionally convergent.

APPROXIMATING THE LIMIT OF AN ALTERNATING SERIES

Evaluating the sum of the first n terms of an alternating series, given by yields an approximation of the limit, L. The error (the difference between the approximation and the true limit) is called the remainder after n terms and is denoted by R_n. When an alternating series is first shown to pass the Alternating Series Test, it’s easy to place an upper bound on this remainder. Because the terms alternate in sign and become progressively smaller in magnitude, an alternating series converges on its limit by oscillation, as shown in Figure N10–1.

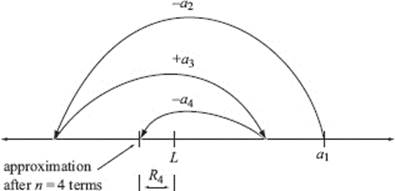
FIGURE N10–1

Error bound

Because carrying out the approximation one more term would once more carry us beyond L, we see that the error is always less than that next term. Since |R_n | < a_{n + 1}, the error bound for an alternating series is the first term omitted or dropped.

EXAMPLE 31

The series passes the Alternating Series Test; hence its sum differs from the sum

by less than which is the error bound.

EXAMPLE 32

How many terms must be summed to approximate to three decimal places the value of

SOLUTION: Since the series converges by the Alternating Series Test; therefore after summing a number of terms the remainder (error) will be less than the first omitted term.

We seek n such that Thus n must satisfy (n + 1)² > 1000, or n > 30.623. Therefore 31 terms are needed for the desired accuracy.