Calculus AB and Calculus BC
CHAPTER 11 Miscellaneous Multiple-Choice Practice Questions
These questions provide further practice for Parts A and B of Section I of the examination.
Part A. Directions: Answer these questions without using your calculator.
1. Which of the following functions is continuous at x = 0?
(A) 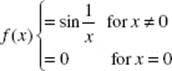
(B) f (x) = [x] (greatest-integer function)
(C) 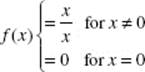
(D) 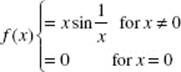
(E) ![]()
2. Which of the following statements about the graph of ![]() is not true?
is not true?
(A) The graph is symmetric to the y-axis.
(B) The graph has two vertical asymptotes.
(C) There is no y-intercept.
(D) The graph has one horizontal asymptote.
(E) There is no x-intercept.
3. ![]()
(A) −1
(B) 0
(C) 1
(D) 2
(E) none of these
4. The x-coordinate of the point on the curve y = x2 − 2x + 3 at which the tangent is perpendicular to the line x + 3y + 3 = 0 is
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) none of these
5. 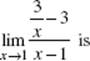
(A) −3
(B) −1
(C) 1
(D) 3
(E) nonexistent
6. For polynomial function p, p ″(2) = −6, p ″(4) = 0, and p ″(5) = 3. Then p must:
(A) have an inflection point at x = 4
(B) have a minimum at x = 4
(C) have a root at x = 4
(D) be increasing on [2,5]
(E) none of these
7. ![]()
(A) 6
(B) 8
(C) 10
(D) 11
(E) 12
8. ![]()
(A) ![]()
(B) ![]()
(C) 1
(D) 3
(E) nonexistent
9. The maximum value of the function f (x) = x4 − 4x3 + 6 on [1, 4] is
(A) 1
(B) 0
(C) 3
(D) 6
(E) none of these
10. Let 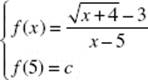 if x ≠ 5, and let f be continuous at x = 5. Then c =
if x ≠ 5, and let f be continuous at x = 5. Then c =
(A) ![]()
(B) 0
(C) ![]()
(D) 1
(E) 6
11. ![]()
(A) −1
(B) ![]()
(C) 0
(D) ![]()
(E) 1
12. If sin x = ln y and 0 < x < π, then, in terms of x, ![]() equals
equals
(A) esin x cos x
(B) e−sin x cos x
(C) ![]()
(D) ecos x
(E) esin x
13. If f (x) = x cos x, then ![]() equals
equals
(A) ![]()
(B) 0
(C) −1
(D) ![]()
(E) 1
14. The equation of the tangent to the curve y = ex ln x, where x = 1, is
(A) y = ex
(B) y = ex + 1
(C) y = e(x − 1)
(D) y = ex + 1
(E) y = x − 1
15. If the displacement from the origin of a particle moving along the x-axis is given by s = 3 + (t − 2)4, then the number of times the particle reverses direction is
(A) 0
(B) 1
(C) 2
(D) 3
(E) none of these
16. ![]() equals
equals
(A) 1 − e
(B) ![]()
(C) e − 1
(D) ![]()
(E) e + 1
17. If 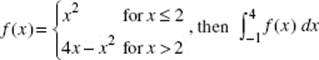 equals
equals
(A) 7
(B) ![]()
(C) ![]()
(D) 9
(E) ![]()
18. If the position of a particle on a line at time t is given by s = t3 + 3t, then the speed of the particle is decreasing when
(A) − 1 < t < 1
(B) − 1 < t < 0
(C) t < 0
(D) t > 0
(E) |t| > 1
19. A rectangle with one side on the x-axis is inscribed in the triangle formed by the lines y = x, y = 0, and 2x + y = 12. The area of the largest such rectangle is
(A) 6
(B) 3
(C) ![]()
(D) 5
(E) 7
CHALLENGE
20. The x-value of the first-quadrant point that is on the curve of x2 − y2 = 1 and closest to the point (3, 0) is
(A) 1
(B) ![]()
(C) 2
(D) 3
(E) none of these
21. If y = ln(4x + 1), then ![]() is
is
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
22. The region bounded by the parabolas y = x2 and y = 6x − x2 is rotated about the x-axis so that a vertical line segment cut off by the curves generates a ring. The value of x for which the ring of largest area is obtained is
(A) 4
(B) 3
(C) ![]()
(D) 2
(E) ![]()
23. ![]() equals
equals
(A) ln (ln x) + C
(B) ![]()
(C) ![]()
(D) ln x + C
(E) none of these
24. The volume obtained by rotating the region bounded by x = y2 and x = 2 − y2 about the y-axis is equal to
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
25. The general solution of the differential equation ![]() is a family of
is a family of
(A) straight lines
(B) circles
(C) hyperbolas
(D) parabolas
(E) ellipses
26. Estimate ![]() dx using the Left Rectangular Rule and two subintervals of equal width.
dx using the Left Rectangular Rule and two subintervals of equal width.
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
27. ![]()
(A) −2
(B) ![]()
(C) 0
(D) ![]()
(E) ![]()
28. ![]()
(A) 0
(B) ![]()
(C) ![]()
(D) ![]()
(E) ∞
BC ONLY
29. ![]()
(A) 0
(B) ![]()
(C) 1
(D) 2
(E) ∞
30. The number of values of k for which f (x) = ex and g(x) = k sin x have a common point of tangency is
(A) 0
(B) 1
(C) 2
(D) large but finite
(E) infinite
CHALLENGE
31. The curve 2x2 y + y2 = 2x + 13 passes through (3, 1). Use the line tangent to the curve there to find the approximate value of y at x = 2.8.
(A) 0.5
(B) 0.9
(C) 0.95
(D) 1.1
(E) 1.4
32. ![]()
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
33. The region bounded by y = tan x, y = 0, and ![]() is rotated about the x-axis. The volume generated equals
is rotated about the x-axis. The volume generated equals
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) none of these
34. ![]() for the constant a > 0, equals
for the constant a > 0, equals
(A) 1
(B) a
(C) ln a
(D) log10 a
(E) a ln a
35. Solutions of the differential equation whose slope field is shown here are most likely to be
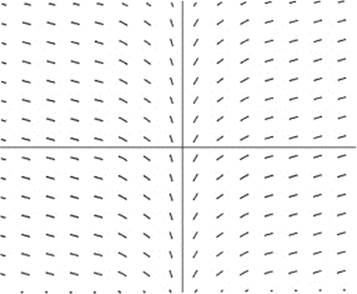
(A) quadratic
(B) cubic
(C) sinusoidal
(D) exponential
(E) logarithmic
36. ![]()
(A) 0
(B) 1
(C) ![]()
(D) ![]()
(E) ![]()
37. The graph of g, shown below, consists of the arcs of two quarter-circles and two straight-line segments. The value of ![]() is
is
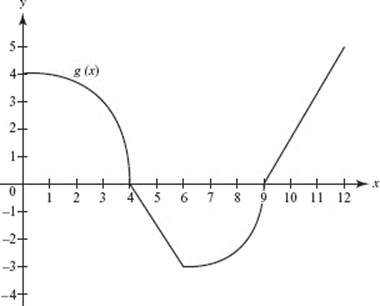
(A) π + 2
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
38. Which of these could be a particular solution of the differential equation whose slope field is shown here?
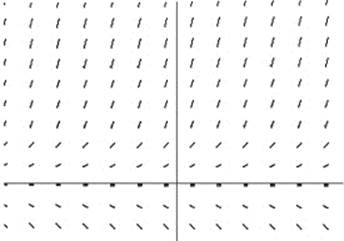
(A) ![]()
(B) y = ln x
(C) y = ex
(D) y = e−x
(E) y = ex2
39. What is the domain of the particular solution for ![]() containing the point where x = −1?
containing the point where x = −1?
(A) x < 0
(B) x > −2
(C) − 2 < x < 2
(D) x ≠ ±2
(E) none of these; no solution exists for x = −1
40. The slope field shown here is for the differential equation
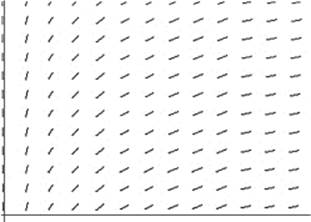
(A) ![]()
(B) y ′ = ln x
(C) y ′ = ex
(D) y ′ = y
(E) y ′ = −y2
41. If we substitute x = tan θ, which of the following is equivalent to ![]()
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
42. If x = 2 sin u and y = cos 2u, then a single equation in x and y is
(A) x2 + y2 = 1
(B) x2 + 4y2 = 4
(C) x2 + 2y = 2
(D) x2 + y2 = 4
(E) x2 − 2y = 2
BC ONLY
43. The area bounded by the lemniscate with polar equation r2 = 2 cos 2θ is equal to
(A) 4
(B) 1
(C) ![]()
(D) 2
(E) none of these
44. ![]()
(A) 0
(B) ![]()
(C) π
(D) 2π
(E) none of these
45. The first four terms of the Maclaurin series (the Taylor series about x = 0) for ![]() are
are
(A) 1 + 2x + 4x2 + 8x3
(B) 1 − 2x + 4x2 − 8x3
(C) − 1 − 2x − 4x2 − 8x3
(D) 1 − x + x2 − x3
(E) 1 + x + x2 + x3
46. ![]()
(A) ![]()
(B) ![]()
(C) −x2 e−x + 2xe−x + C
(D) −x2 e−x − 2xe−x − 2e−x + C
(E) −x2 e−x + 2xe−x − 2e−x + C
47. ![]() is equal to
is equal to
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
BC ONLY
48. A curve is given parametrically by the equations x = t, y = 1 − cos t. The area bounded by the curve and the x-axis on the interval 0 ![]() t
t ![]() 2π is equal to
2π is equal to
(A) 2(π + 1)
(B) π
(C) 4π
(D) π + 1
(E) 2π
49. If x = a cot θ and y = a sin2 θ, then ![]() when
when ![]() is equal to
is equal to
(A) ![]()
(B) −1
(C) 2
(D) ![]()
(E) ![]()
50. Which of the following improper integrals diverges?
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
51. ![]()
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
52. ![]()
(A) −∞
(B) 0
(C) 1
(D) ∞
(E) nonexistent
53. A particle moves along the parabola x = 3y − y2 so that ![]() at all time t. The speed of the particle when it is at position (2, 1) is equal to
at all time t. The speed of the particle when it is at position (2, 1) is equal to
(A) 0
(B) 3
(C) ![]()
(D) ![]()
(E) none of these
54. ![]()
(A) −∞
(B) −1
(C) 0
(D) 1
(E) ∞
55. When rewritten as partial fractions, ![]() includes which of the following?
includes which of the following?
I. ![]()
II. ![]()
III. ![]()
(A) none
(B) I only
(C) II only
(D) III only
(E) I and III
56. Using two terms of an appropriate Maclaurin series, estimate ![]()
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) undefined; the integral is improper
BC ONLY
57. The slope of the spiral r = θ at ![]()
(A) ![]()
(B) −1
(C) 1
(D) ![]()
(E) undefined
Part B. Directions: Some of these questions require the use of a graphing calculator.
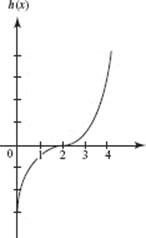
58. The graph of function h is shown here. Which of these statements is (are) true?
I. The first derivative is never negative.
II. The second derivative is constant.
III. The first and second derivatives equal 0 at the same point.
(A) I only
(B) III only
(C) I and II
(D) I and III
(E) all three
59. Graphs of functions f (x), g(x), and h(x) are shown below.
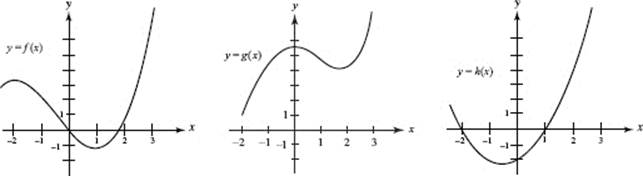
Consider the following statements:
I. g(x) = f ′(x)
II. f (x) = g ′(x)
III. h(x) = g ″(x)
Which of these statements is (are) true?
(A) I only
(B) II only
(C) II and III only
(D) all three
(E) none of these
60. ![]()
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) 0
61. If ![]()
(A) −6
(B) −5
(C) 5
(D) 6
(E) 7
62. At what point in the interval [1, 1.5] is the rate of change of f (x) = sin x equal to its average rate of change on the interval?
(A) 0.995
(B) 1.058
(C) 1.239
(D) 1.253
(E) 1.399
63. Suppose f ′(x) = x2 (x − 1). Then f ″(x) = x (3x − 2). Over which interval(s) is the graph of f both increasing and concave up?
I. x < 0
II. ![]()
III. ![]()
IV. x > 1
(A) I only
(B) II only
(C) II and IV
(D) I and III
(E) IV only
64. Which of the following statements is true about the graph of f (x) in Question 62?
(A) The graph has no relative extrema.
(B) The graph has one relative extremum and one inflection point.
(C) The graph has two relative extrema and one inflection point.
(D) The graph has two relative extrema and two inflection points.
(E) None of the preceding statements is true.
65. The nth derivative of ln (x + 1) at x = 2 equals
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
66. If f (x) is continuous at the point where x = a, which of the following statements may be false?
(A) ![]()
(B) ![]()
(C) f ′(a) exists.
(D) f (a) is defined.
(E) ![]()
67. Suppose ![]() where k is a constant. Then
where k is a constant. Then ![]() equals
equals
(A) 3
(B) 4 − k
(C) 4
(D) 4 + k
(E) none of these
68. The volume, in cubic feet, of an “inner tube” with inner diameter 4 ft and outer diameter 8 ft is
(A) 4π2
(B) 12π2
(C) 8π2
(D) 24π2
(E) 6π2
CHALLENGE
69. If f (u) = tan−1 u2 and g(u) = eu, then the derivative of f (g (u)) is
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
70. If sin (xy) = y, then ![]() equals
equals
(A) sec (xy)
(B) y cos (xy) − 1
(C) ![]()
(D) ![]()
(E) cos (xy)
71. Let x > 0. Suppose ![]()
(A) f (x4)
(B) f (x2)
(C) 2xg(x2)
(D) ![]()
(E) 2g(x2) + 4x2 f (x)
72. The region bounded by y = ex, y = 1, and x = 2 is rotated about the x-axis. The volume of the solid generated is given by the integral
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
73. Suppose the function f is continuous on 1 ![]() x
x ![]() 2, that f ′(x) exists on 1 < x < 2, that f (1) = 3, and that f (2) = 0. Which of the following statements is not necessarily true?
2, that f ′(x) exists on 1 < x < 2, that f (1) = 3, and that f (2) = 0. Which of the following statements is not necessarily true?
(A) The Mean-Value Theorem applies to f on 1 ![]() x
x ![]() 2.
2.
(B) ![]() exists.
exists.
(C) There exists a number c in the closed interval [1,2] such that f ′(c) = 0.
(D) If k is any number between 0 and 3, there is a number c between 1 and 2 such that f (c) = k.
(E) If c is any number such that 1 < c < 2, then ![]() exists.
exists.
74. The region S in the figure is bounded by y = sec x, the y-axis, and y = 4. What is the volume of the solid formed when S is rotated about the y-axis?
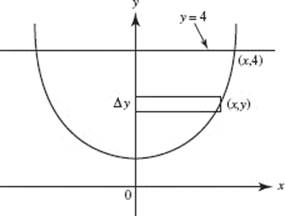
(A) 0.791
(B) 2.279
(C) 5.692
(D) 11.385
(E) 17.217
75. If 40 g of a radioactive substance decomposes to 20 g in 2 yr, then, to the nearest gram, the amount left after 3 yr is
(A) 10
(B) 12
(C) 14
(D) 16
(E) 17
76. An object in motion along a line has acceleration ![]() and is at rest when t = 1. Its average velocity from t = 0 to t = 2 is
and is at rest when t = 1. Its average velocity from t = 0 to t = 2 is
(A) 0.362
(B) 0.274
(C) 3.504
(D) 7.008
(E) 8.497
77. Find the area bounded by y = tan x and x + y = 2, and above the x-axis on the interval [0, 2],
(A) 0.919
(B) 0.923
(C) 1.013
(D) 1.077
(E) 1.494
78. An ellipse has major axis 20 and minor axis 10. Rounded off to the nearest integer, the maximum area of an inscribed rectangle is
(A) 50
(B) 79
(C) 80
(D) 82
(E) 100
79. The average value of y = x ln x on the interval 1 ![]() x
x ![]() e is
e is
(A) 0.772
(B) 1.221
(C) 1.359
(D) 1.790
(E) 2.097
80. Let ![]() for 0
for 0 ![]() x
x ![]() 2π. On which interval is f increasing?
2π. On which interval is f increasing?
(A) 0 < x < π
(B) 0.654 < x < 5.629
(C) 0.654 < x < 2π
(D) π < x < 2π
(E) none of these
81. The table shows the speed of an object (in ft/sec) during a 3-sec period. Estimate its acceleration (in ft/sec2) at t = 1.5 sec.
|
time, sec |
0 |
1 |
2 |
3 |
|
speed, ft/sec |
30 |
22 |
12 |
0 |
(A) −17
(B) −13
(C) −10
(D) −5
(E) 17
82. A maple-syrup storage tank 16 ft high hangs on a wall. The back is in the shape of the parabola y = x2 and all cross sections parallel to the floor are squares. If syrup is pouring in at the rate of 12 ft3 /hr, how fast (in ft/hr) is the syrup level rising when it is 9 ft deep?
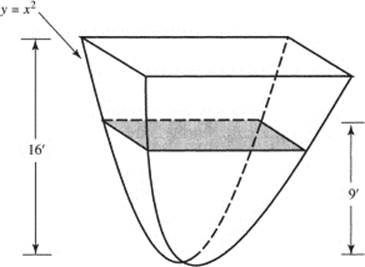
(A) ![]()
(B) ![]()
(C) ![]()
(D) 36
(E) 162
83. In a protected area (no predators, no hunters), the deer population increases at a rate of ![]() where P(t) represents the population of deer at t yr. If 300 deer were originally placed in the area and a census showed the population had grown to 500 in 5 yr, how many deer will there be after 10 yr?
where P(t) represents the population of deer at t yr. If 300 deer were originally placed in the area and a census showed the population had grown to 500 in 5 yr, how many deer will there be after 10 yr?
(A) 608
(B) 643
(C) 700
(D) 833
(E) 892
84. Shown is the graph of ![]()
Let ![]() The local linearization of H at x = 1 is H(x) equals
The local linearization of H at x = 1 is H(x) equals
(A) 2x
(B) −2x − 4
(C) 2x + π − 2
(D) −2x + π + 2
(E) 2x + ln 16 + 2
85. A smokestack 100 ft tall is used to treat industrial emissions. The diameters, measured at 25-ft intervals, are shown in the table. Using the midpoint rule, estimate the volume of the smokestack to the nearest 100 ft3.
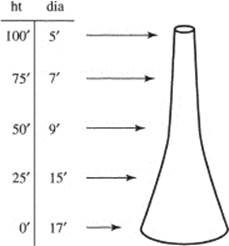
(A) 8100
(B) 9500
(C) 9800
(D) 12,500
(E) 39,300
For Questions 86–90 the table shows the values of differentiable functions f and g.
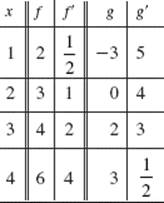
86. If ![]() then P ′(3) =
then P ′(3) =
(A) −2
(B) ![]()
(C) ![]()
(D) ![]()
(E) 2
87. If H(x) = f (g (x)), then H ′(3) =
(A) 1
(B) 2
(C) 3
(D) 6
(E) 9
88. If M(x) = f (x) · g (x), then M ′(3) =
(A) 2
(B) 6
(C) 8
(D) 14
(E) 16
89. If K(x) = g−1 (x), then K ′(3) =
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) 2
90. If R (x) = ![]() then R ′(3) =
then R ′(3) =
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) 2
91. Water is poured into a spherical tank at a constant rate. If W(t) is the rate of increase of the depth of the water, then W is
(A) constant
(B) linear and increasing
(C) linear and decreasing
(D) concave up
(E) concave down
92. The graph of f ′ is shown below. If f (7) = 3 then f (1) =
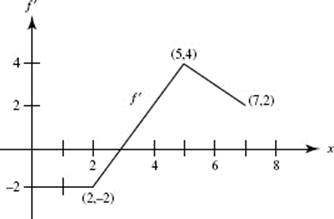
(A) −10
(B) −4
(C) −3
(D) 10
(E) 16
93. At an outdoor concert, the crowd stands in front of the stage filling a semicircular disk of radius 100 yd. The approximate density of the crowd x yd from the stage is given by
![]()
people per square yard. About how many people are at the concert?
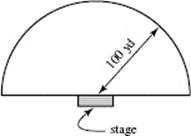
(A) 200
(B) 19,500
(C) 21,000
(D) 165,000
(E) 591,000
94. The Centers for Disease Control announced that, although more AIDS cases were reported this year, the rate of increase is slowing down. If we graph the number of AIDS cases as a function of time, the curve is currently
(A) increasing and linear
(B) increasing and concave down
(C) increasing and concave up
(D) decreasing and concave down
(E) decreasing and concave up
The graph below is for Questions 95–97. It shows the velocity, in feet per second, for 0 < t < 8, of an object moving along a straight line.
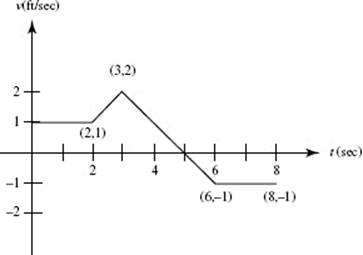
95. The object’s average speed (in ft/sec) for this 8-sec interval was
(A) 0
(B) ![]()
(C) 1
(D) ![]()
(E) 8
96. When did the object return to the position it occupied at t = 2?
(A) t = 4
(B) t = 5
(C) t = 6
(D) t = 8
(E) never
97. The object’s average acceleration (in ft/sec2) for this 8-sec interval was
(A) −2
(B) ![]()
(C) 0
(D) ![]()
(E) 1
98. If a block of ice melts at the rate of ![]() cm3 /min, how much ice melts during the first 3 min?
cm3 /min, how much ice melts during the first 3 min?
(A) 8 cm3
(B) 16 cm3
(C) 21 cm3
(D) 40 cm3
(E) 79 cm3
99. A particle moves counterclockwise on the circle x2 + y2 = 25 with a constant speed of 2 ft/sec. Its velocity vector, v, when the particle is at (3, 4), equals
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
BC ONLY
100. Let R = a cos kti + a sin ktj be the (position) vector xi + yj from the origin to a moving point P(x, y) at time t, where a and k are positive constants. The acceleration vector, a, equals
(A) −k2 R
(B) a2 k2 R
(C) −aR
(D) ![]()
(E) −R
101. The length of the curve y = 2x between (0, 1) and (2, 4) is
(A) 3.141
(B) 3.664
(C) 4.823
(D) 5.000
(E) 7.199
102. The position of a moving object is given by P(t) = (3t, et). Its acceleration is
(A) undefined
(B) constant in both magnitude and direction
(C) constant in magnitude only
(D) constant in direction only
(E) constant in neither magnitude nor direction
BC ONLY
103. Suppose we plot a particular solution of ![]() from initial point (0, 1) using Euler’s method. After one step of size Δx = 0.1, how big is the error?
from initial point (0, 1) using Euler’s method. After one step of size Δx = 0.1, how big is the error?
(A) 0.09
(B) 1.09
(C) 1.49
(D) 1.90
(E) 2.65
104. We use the first three terms to estimate ![]() Which of the following statements is (are) true?
Which of the following statements is (are) true?
I. The estimate is 0.7.
II. The estimate is too low.
III. The estimate is off by less than 0.1.
(A) I only
(B) III only
(C) I and II
(D) I and III
(E) all three
105. Which of these diverges?
(A) ![]()
(B) 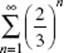
(C) ![]()
(D) ![]()
(E) ![]()
106. Find the radius of convergence of ![]()
(A) 0
(B) ![]()
(C) 1
(D) e
(E) ∞
107. When we use ![]() to estimate
to estimate ![]() the Lagrange remainder is no greater than
the Lagrange remainder is no greater than
(A) 0.021
(B) 0.034
(C) 0.042
(D) 0.067
(E) 0.742
108. An object in motion along a curve has position P(t) = (tan t, cos 2t) for 0 ![]() t
t ![]() 1. How far does it travel?
1. How far does it travel?
(A) 0.96
(B) 1.73
(C) 2.10
(D) 2.14
(E) 3.98