Calculus AB and Calculus BC

BC Practice Examination 2

SECTION I

Part A TIME: 55 MINUTES

The use of calculators is not permitted for this part of the examination. There are 28 questions in Part A, for which 55 minutes are allowed. Because there is no deduction for wrong answers, you should answer every question, even if you need to guess.

Directions: Choose the best answer for each question.

1. A function f (x) equals for all x except x = 1. For the function to be continuous at x = 1, the value of f (1) must be

(A) 0

(B) 1

(C) 2

(D) ∞

(E) none of these

2.

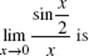
(A) 2

(B) 0

(C)

(D) 1

(E) nonexistent

3. The first four terms of the Taylor series about x = 0 of are

(A)

(B)

(C)

(D)

(E)

4. Using the line tangent to at x = 0, an estimate of f (0.06) is

(A) 0.02

(B) 2.98

(C) 3.01

(D) 3.02

(E) 3.03

5. Air is escaping from a balloon at a rate of cubic feet per minute, where t is measured in minutes. How much air, in cubic feet, escapes during the first minute?

(A) 15

(B) 15π

(C) 30

(D) 30π

(E) 30 ln 2

6. The motion of a particle in a plane is given by the pair of equations x = cos 2t, y = sin 2t. The magnitude of its acceleration at any time t equals

(A) 2

(B)

(C) 4

(D)

(E) 16

7. Let

The interval of convergence of f ′(x) is

(A) 0 x 2

(B) 0 x < 2

(C) 0 < x 2

(D) 0 < x < 2

(E) only x = 1

8. A point moves along the curve y = x² + 1 so that the x-coordinate is increasing at the constant rate of units per second. The rate, in units per second, at which the distance from the origin is changing when the point has coordinates (1,2) is equal to

(A)

(B)

(C)

(D)

(E)

9.

(A) = 0

(B)

(C) = 1

(D) = 10

(E) does not exist

10. sec² x tan² x dx equals

(A)

(B)

(C)

(D) 3

(E)

11. equals

(A)

(B) e − 1

(C) e + 1

(D) 1

(E) −1

12.

(A)

(B) y² −y + ln|2y| + C

(C)

(D)

(E)

13.

(A) ln |x² (x − 3)| + C

(B) −ln |x² (x − 3)| + C

(C)

(D)

(E) none of these

14. Given f ′ as graphed, which could be a graph of f ?

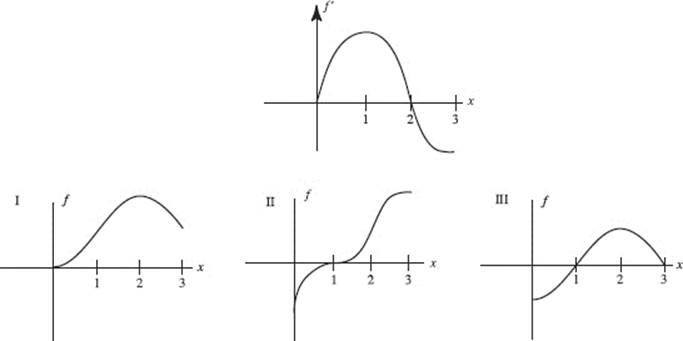
(A) I only

(B) II only

(C) III only

(D) I and III

(E) none of these

15. The first woman officially timed in a marathon was Violet Piercey of Great Britain in 1926. Her record of 3:40:22 stood until 1963, mostly because of a lack of women competitors. Soon after, times began dropping rapidly, but lately they have been declining at a much slower rate. LetM(t) be the curve that best represents winning marathon times in year t. Which of the following is negative?

I. M(t)

II. M ′(t)

III. M ″(t)

(A) I only

(B) II only

(C) III only

(D) II and III

(E) none of these

16. The graph of f is shown above. Let Which of the following is true?

(A) G(x) = H(x)

(B) G ′(x) = H ′(x + 2)

(C) G(x) = H(x + 2)

(D) G(x) = H(x) − 2

(E) G(x) = H(x) + 3

17. The minimum value of on the interval x 2 is

(A)

(B) 1

(C) 3

(D)

(E) 5

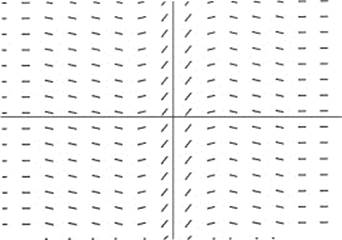
18. Which function could be a particular solution of the differential equation whose slope field is shown above?

(A) y = x³

(B)

(C)

(D) y = sin x

(E) y = e ^−x2

19. A particular solution of the differential equation = x + y passes through the point (2,1). Using Euler’s method with Δx = 0.1, estimate its y-value at x = 2.2.

(A) 0.34

(B) 1.30

(C) 1.34

(D) 1.60

(E) 1.64

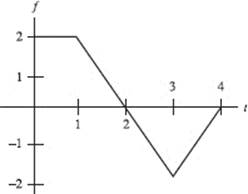
Questions 20 and 21. Use the graph below, consisting of two line segments and a quarter-circle. The graph shows the velocity of an object during a 6-second interval.

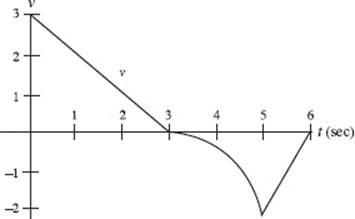
20. For how many values of t in the interval 0 < t < 6 is the acceleration undefined?

(A) none

(B) one

(C) two

(D) three

(E) four

21. During what time interval (in sec) is the speed increasing?

(A) 0 < t < 3

(B) 3 < t < 5

(C) 3 < t < 6

(D) 5 < t < 6

(E) never

22. If and y = 3 when x = 1, then

(A) x² + y² = 10

(B) y = x + ln3

(C) y² − x² = 8

(D) y = 3x

(E) y² − 3x² = 6

23. A solid is cut out of a sphere of radius 2 by two parallel planes each 1 unit from the center. The volume of this solid is

(A) 8π

(B)

(C)

(D)

(E)

24. Which one of the following improper integrals converges?

(A)

(B)

(C)

(D)

(E) none of these

25. Let f (x) = x⁵ + 3x − 2, and let f ⁻¹ denote the inverse of f. Then (f ⁻¹) ′(2) equals

(A)

(B)

(C) 1

(D) 8

(E) 83

26. Find the domain of the particular solution of = 1 + y² that passes through the origin.

(A) all x

(B) x ≥ 0

(C)

(D)

(E)

27. Which of the following statements is (are) true about the graph of y = ln (4 + x²)?

I. It is symmetric to the y-axis.

II. It has a local minimum at x = 0.

III. It has inflection points at x = ±2.

(A) I only

(B) II only

(C) III only

(D) I and II only

(E) I, II, and III

28.

(A)

(B)

(C)

(D)

(E) nonexistent

Part B TIME: 50 MINUTES

Some questions in this part of the examination require the use of a graphing calculator. There are 17 questions in Part B, for which 50 minutes are allowed. Because there is no deduction for wrong answers, you should answer every question, even if you need to guess.

Directions: Choose the best answer for each question. If the exact numerical value of the correct answer is not listed as a choice, select the choice that is closest to the exact numerical answer.

29. The area bounded by the curve x = 3y − y² and the line x = − y is represented by

(A)

(B)

(C)

(D)

(E)

30. Find the area bounded by the spiral r = ln θ on the interval π θ 2π.

(A) 2.405

(B) 2.931

(C) 3.743

(D) 4.810

(E) 7.487

31. Write an equation for the line tangent to the curve defined by F(t) = (t² + 1,2^t) at the point where y = 4.

(A) y − 4 = ln 2(x − 2)

(B) y − 4 = 4 ln 2(x − 2)

(C) y − 4 = 4(x − 5)

(D) y − 4 = ln 2(x − 5)

(E) y − 4 = 4 ln 2(x − 5)

32. Which infinite series converge(s)?

I.

II.

III.

(A) I only

(B) II only

(C) III only

(D) I and III only

(E) none of these

33. Bacteria in a culture increase at a rate proportional to the number present. An initial population of 200 triples in 10 hours. If this pattern of increase continues unabated, then the approximate number of bacteria after 1 full day is

(A) 1160

(B) 1440

(C) 2408

(D) 2793

(E) 8380

34. When the substitution x = 2t − 1 is used, the definite integral dt may be expressed in the form where {k. a, b } =

(A)

(B)

(C)

(D)

(E)

35. The curve defined by x³ + xy − y² = 10 has a vertical tangent line when x =

(A)

(B) 1.037

(C) 2.074

(D) 2.096

(E) 2.154

Questions 36 and 37. Use the graph of f shown on [0,7]. Let

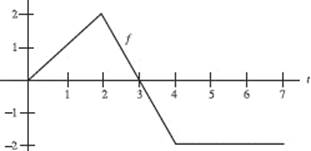
36. G ′(1) is

(A) 1

(B) 2

(C) 3

(D) 6

(E) undefined

37. G has a local maximum at x =

(A) 1

(B)

(C) 2

(D) 5

(E) 8

38. If the half-life of a radioactive substance is 8 years, how long will it take, in years, for two thirds of the substance to decay?

(A) 4.68

(B) 7.69

(C) 12

(D) 12.21

(E) 12.68

39. Using the left rectangular method and four subintervals of equal width, estimate where f is the function graphed below.

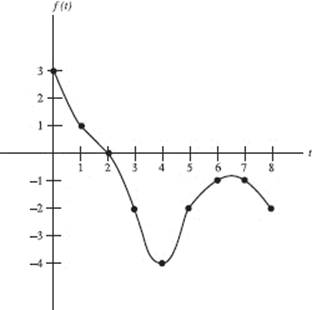
(A) 4

(B) 5

(C) 8

(D) 15

(E) 16

40. The area in the first quadrant bounded by the curve with parametric equations x = 2a tan θ and y = 2a cos² θ, and the lines x = 0 and x = 2a, is equal to

(A) πa²

(B) 2πa²

(C)

(D)

(E) none of these

41. The base of a solid is the region bounded by x² = 4y and the line y = 2, and each plane section perpendicular to the y-axis is a square. The volume of the solid is

(A) 8

(B) 16

(C) 20

(D) 32

(E) 64

42. An object initially at rest at (3,3) moves with acceleration Where is the object at t = 2?

(A) (4,e ⁻²)

(B) (4,e ⁻² + 2)

(C) (7,e ⁻²)

(D) (7,e ⁻² + 2)

(E) (7,e ⁻² + 4)

43. Find the length of the curve y = ln x between the points where and y = 1.

(A) 0.53

(B) 0.86

(C) 1.18

(D) 1.36

(E) 10.02

44. Using the first two terms in the Maclaurin series for y = cos x yields accuracy to within 0.001 over the interval |x| < k when k =

(A) 0.032

(B) 0.394

(C) 0.786

(D) 0.788

(E) 1.570

45. After t years, 50e ^−0.015t pounds of a deposit of a radioactive substance remain. The average amount per year not lost by radioactive decay during the second hundred years is

(A) 2.9 lb

(B) 5.8 lb

(C) 7.4 lb

(D) 11.1 lb

(E) none of these

SECTION II

Part A TIME: 30 MINUTES
2 PROBLEMS

A graphing calculator is required for some of these problems.

1. Let function f be continuous and decreasing, with values as shown in the table:

(a) Use the trapezoid method to estimate the area between f and the x-axis on the interval 2.5 ≤ x ≤ 5.0.

(b) Find the average rate of change of f on the interval 2.5 ≤ x ≤ 5.0.

(c) Estimate the instantaneous rate of change of f at x = 2.5.

(d) If g(x) = f ⁻¹(x), estimate the slope of g at x = 4.

2. An object starts at point (1,3), and moves along the parabola y = x² + 2 for 0 ≤ t ≤ 2, with the horizontal component of its velocity given by

(a) Find the object’s position at t = 2.

(b) Find the object’s speed at t = 2.

(c) Find the distance the object traveled during this interval.

Part B TIME: 60 MINUTES
4 PROBLEMS

No calculator is allowed for any of these problems.
If you finish Part B before time has expired, you may return to work on Part A, but you may not use a calculator.

3. Given a function f such that f (3) = 1 and

(a) Write the first four nonzero terms and the general term of the Taylor series for f around x = 3.

(b) Find the radius of convergence of the Taylor series.

(c) Show that the third-degree Taylor polynomial approximates f (4) to within 0.01.

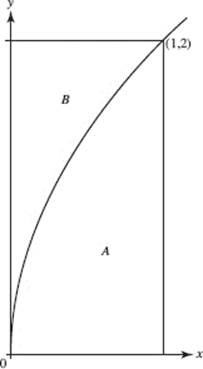
4. The curve divides a first quadrant rectangle into regions A and B, as shown in the figure.

(a) Region A is the base of a solid. Cross sections of this solid perpendicular to the x-axis are rectangles. The height of each rectangle is 5 times the length of its base in region A. Find the volume of this solid.

(b) The other region, B, is rotated around the y-axis to form a different solid. Set up but do not evaluate an integral for the volume of this solid.

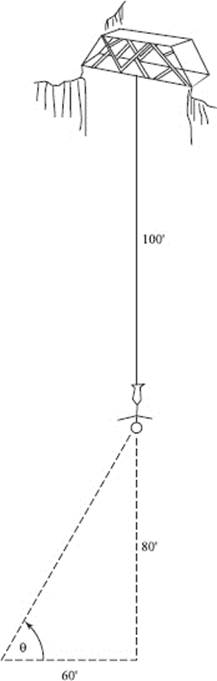
5. A bungee jumper has reached a point in her exciting plunge where the taut cord is 100 feet long with a 1/2-inch radius, and stretching. She is still 80 feet above the ground and is now falling at 40 feet per second. You are observing her jump from a spot on the ground 60 feet from the potential point of impact, as shown in the diagram above.

(a) Assuming the cord to be a cylinder with volume remaining constant as the cord stretches, at what rate is its radius changing when the radius is 1/2″?

(b) From your observation point, at what rate is the angle of elevation to the jumper changing when the radius is 1/2″?

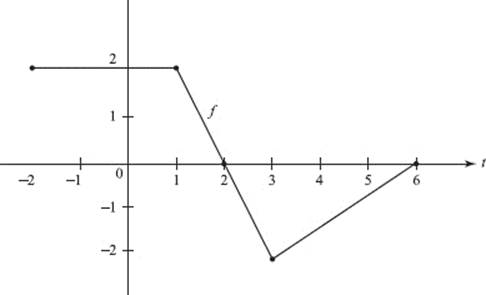
6. The figure above shows the graph of f, whose domain is the closed interval [−2,6]. Let

(a) Find F (−2) and F(6).

(b) For what value(s) of x does F(x) = 0?

(c) For what value(s) of x is F increasing?

(d) Find the maximum value and the minimum value of F.

(e) At what value(s) of x does the graph of F have points of inflection? Justify your answer.