Calculus AB and Calculus BC

Appendix: Formulas and Theorems for Reference

ALGEBRA

1. QUADRATIC FORMULA. The roots of the quadratic equation

ax² + bx + c = 0 (a ≠ 0)

are given by

2. BINOMIAL THEOREM. If n is a positive integer, then

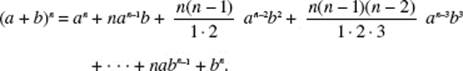
3. REMAINDER THEOREM. If the polynomial Q(x) is divided by (x − a) until a constant remainder R is obtained, then R = Q(a). In particular, if a is a root of Q(x) = 0, then Q(a) = 0.

GEOMETRY

The sum of the angles of a triangle is equal to a straight angle (180°).

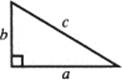
PYTHAGOREAN THEOREM

In the following formulas,

4. Triangle:

5. Trapezoid:

6. Parallelogram: A = bh.

7. Circle: C = 2πr, A = πr².

8. Circular sector:

9. Circular arc: l = rθ.

10. Cylinder:

11. Cone:

12. Sphere:

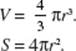
TRIGONOMETRY

BASIC IDENTITIES

13. sin² θ + cos² θ = 1.

14. 1 + tan² θ = sec² θ.

15. 1 + cot² θ = csc² θ.

SUM AND DIFFERENCE FORMULAS

16. sin (α ± β) = sin α cos β ± cos α sin β.

17. cos (α ± β) = cos α cos β sin α sin β.

18.

DOUBLE-ANGLE FORMULAS

19. sin 2α = 2 sin α cos α.

20. cos 2α = cos² α − sin² α = 2 cos² α − 1 = 1 − 2 sin² α.

21.

HALF-ANGLE FORMULAS

22.

23.

REDUCTION FORMULAS

24. sin (−α) = −sin α: cos (−α) = cos α.

25.

26.

27. sin (π − α) = sin α; cos (π − α) = −cos α.

28. sin (π + α) = −sin α; cos (π + α) = −cos α.

29. LAW OF COSINES. c² = a² + b² − 2ab cos C.

30. LAW OF SINES.

31. The area sin C.

GRAPHS OF TRIGONOMETRIC FUNCTIONS

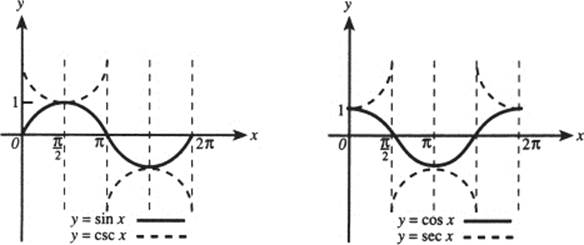
The four functions sketched above, sin, cos, csc, and sec, all have period 2π.

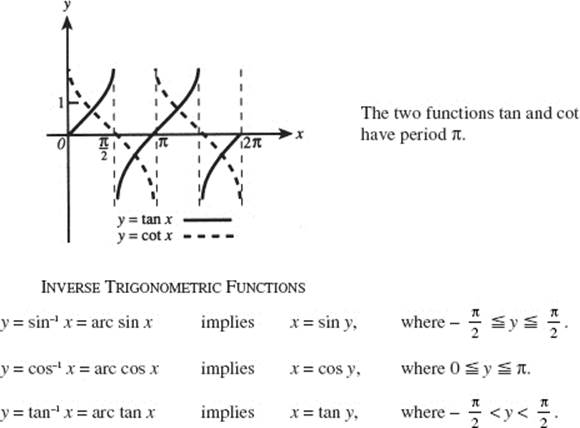
ANALYTIC GEOMETRY

RECTANGULAR COORDINATES

DISTANCE

32. The distance d between two points, P₁ (x₁, y₁) and P₂ (x₂, y₂), is given by

EQUATIONS OF THE STRAIGHT LINE

33. POINT-SLOPE FORM. Through P₁ (x₁, y₁) and with slope m:

y − y₁ = m(x − x₁).

34. SLOPE-INTERCEPT FORM. With slope m and y-intercept b:

y = mx + b.

35. TWO-POINT FORM. Through P₁ (x₁, y₁) and P₂ (x₂, y₂):

36. INTERCEPT FORM. With x- and y-intercepts of a and b, respectively:

37. GENERAL FORM. Ax + By + C = 0, where A and B are not both zero. If B ≠ 0, the slope is the y-intercept, the x-intercept,

DISTANCE FROM POINT TO LINE

38. Distance d between a point P(x₁, y₁) and the line Ax + By + C = 0 is

EQUATIONS OF THE CONICS
CIRCLE

39. With center at (0, 0) and radius r: x² + y² = r².

40. With center at (h, k) and radius r: (x − h)² + (y − k)² = r².

PARABOLA

41. With vertex at (0, 0) and focus at (p, 0): y² = 4px.

42. With vertex at (0, 0) and focus at (0, p): x² = 4py.

With vertex at (h, k) and axis

43. parallel to x-axis, focus at (h + p, k): (y − k)² = 4p(x − h).

44. parallel to y-axis, focus at (h, k + p): (x − h)² = 4p(y − k).

ELLIPSE

With major axis of length 2a, minor axis of length 2b, and distance between foci of 2c:

45. Center at (0, 0), foci at (±c, 0), and vertices at (±a, 0):

46. Center at (0, 0), foci at (0, ±c), and vertices at (0, ±a):

47. Center at (h, k), major axis horizontal, and vertices at (h ± a, k):

48. Center at (h, k), major axis vertical, and vertices at (h, k ± a):

For the ellipse, a² = b² + c², and the eccentricity which is less than 1.

HYPERBOLA

With real (transverse) axis of length 2a, imaginary (conjugate) axis of length 2b, and distance between foci of 2c:

49. Center at (0, 0), foci at (±c, 0), and vertices at (±a, 0):

50. Center at (0, 0), foci at (0, ±c), and vertices at (0, ±a):

51. Center at (h, k), real axis horizontal, vertices at (h ± a, k):

52. Center at (h, k), real axis vertical, vertices at (h, k± a):

For the hyperbola, c² = a² + b², and eccentricity which is greater than 1.

POLAR COORDINATES

RELATIONS WITH RECTANGULAR COORDINATES

53. x = r cos θ;

y = r sin θ;

r² = x² + y²;

SOME POLAR EQUATIONS

54. r = a circle, center at pole, radius a.

55. r = 2a cos θ circle, center at (a, 0), radius a.

56. r = 2a sin θ circle, center at (0, a), radius a.

57.

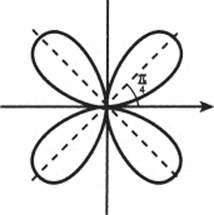
58.

roses (four leaves)

59. r = cos 2θ.

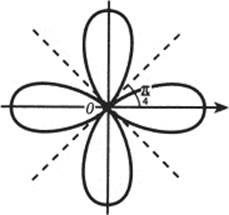
60. r = sin 2θ.

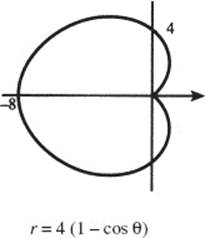
cardioids (specific examples below)

61. r = a (1 ± cos θ).

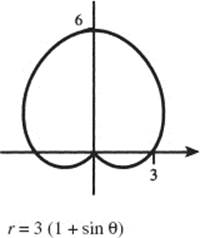
62. r = a (1 ± sin θ).

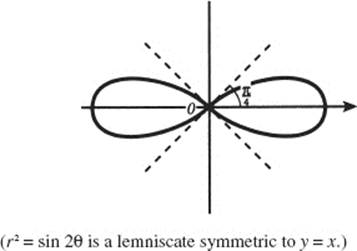
63. r² = cos 2θ, lemniscate, symmetric to the x-axis.

64. r = θ, (double) spiral of Archimedes

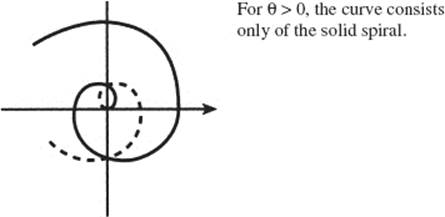
65. rθ = a (θ > 0), hyperbolic (or reciprocal) spiral

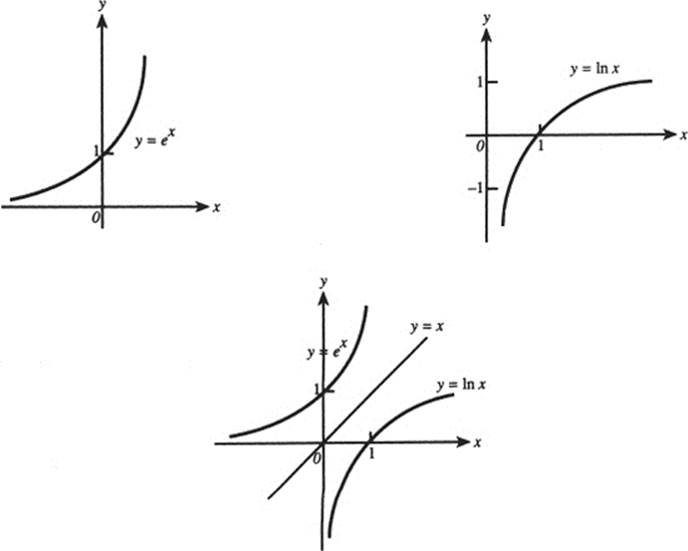
EXPONENTIAL AND LOGARITHMIC FUNCTIONS

PROPERTIES

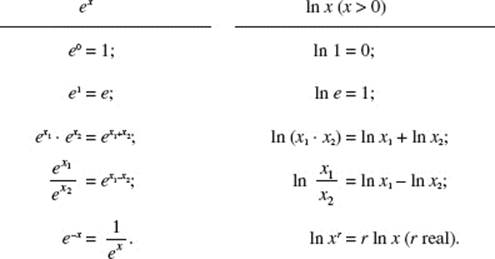
INVERSE PROPERTIES

f (x) = e^x and f ⁻¹(x) = ln x are inverses of each other:

f ⁻¹(f (x)) = f (f ⁻¹(x)) = x;

ln e^x = e^{ln x} = x(x > 0).

GRAPHS