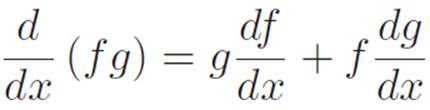Burn Math Class: And Reinvent Mathematics for Yourself (2016)

3. As If Summoned from the Void

And every science, when we understand it not as an instrument of power and domination but as an adventure in knowledge pursued by our species across the ages, is nothing but this harmony, more or less vast, more or less rich from one epoch to another, which unfurls over the course of generations and centuries, by the delicate counterpoint of all the themes appearing in turn, as if summoned from the void.

—Alexander Grothendieck, Récoltes et Semailles

3.1. Who Ordered That?

3.1.1From an Abbreviation to an Idea. . . By Accident

In Interlude 2, we discovered something quite strange. Originally we introduced (stuff)ⁿ as an abbreviation. That is, we simply defined

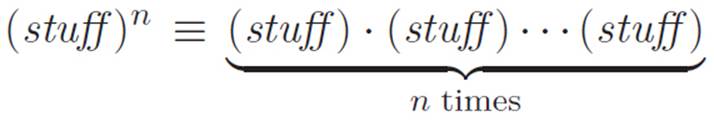
As long as this was all we meant by raising something to a power, we could be confident that there was nothing about the concept of powers that we didn’t understand. After all, powers were not really a concept to begin with. They were a completely vacuous and content-free abbreviation. There was simply nothing to know about them. However, in extending this (non-)concept to powers other than positive whole numbers, we performed a strange feat of mathematical creation. We said:

I have no idea what (stuff)^# means when # isn’t a whole number. . .

But I really want to hold on to the sentence

(stuff)^n+m = (stuff)ⁿ(stuff)^m

So I’ll force (stuff)^# to mean:

whatever it has to mean in order to make that sentence keep being true.

By attempting to extend a vacuous non-concept to a non-vacuous concept, we found that we had unwittingly summoned from the void an idea about which there was something to know, and with which we were not familiar. Having performed what appeared to be nothing but a harmless act of generalization and abstraction, we found that we had created a new and unexplored part of our universe. After a brief exploration of it, we proceeded to discover three simple facts about our accidental conceptual progeny.

We discovered that we had forced the following to be true:

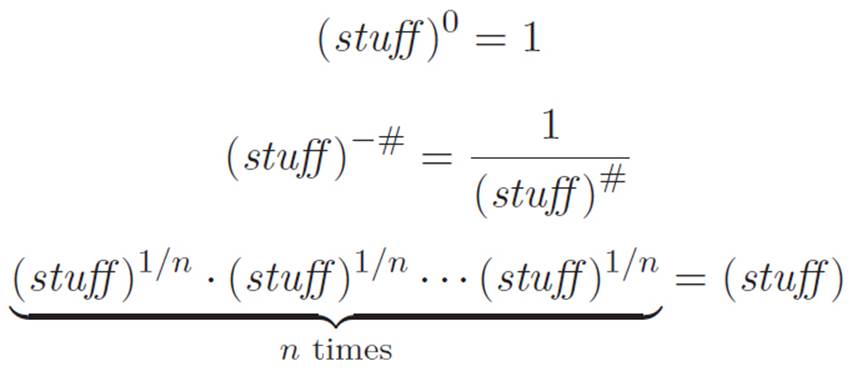
We have no reason to expect that the above constitutes a complete map of the world we accidentally invented. For example, by creating negative and fractional powers, we also accidentally created a unexplored swarm of new machines.

New machines that must now exist, as a consequence of our invention:

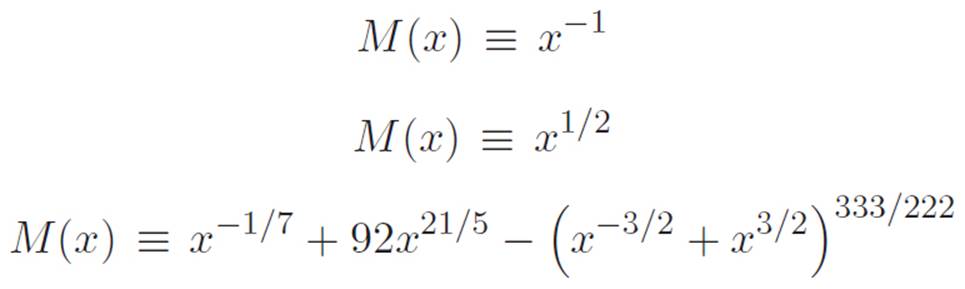
The third example above makes it clear just how large this new and unexplored corner of our universe really is. And just when we were starting to feel accomplished! Recall that at the end of Chapter 2, we not only thought of a way to abbreviate all of the machines that our universe contained at that point — the plus-times machines — but we also managed to figure out how to differentiate any (and thus all) of them, by pulling the clever trick of differentiating our abbreviation that stood for an arbitrary one of them (thus differentiating all of them simultaneously).

To stress just how much larger our world has suddenly become, notice that presumably all of these machines have derivatives. At this point we know none of them, even though it was we who conjured up this world. Mathematics is strange. . .Well, let’s take a nap to try to wrap our minds around the immensity of what we’ve done, and when we wake up, maybe we’ll have the energy to play with a few of these machines for a while and see if we want to acknowledge them, or if we would prefer to simply pretend that they don’t exist.

3.1.2Visualizing Some of These Beasts

In keeping with the spirit of creating mathematics from the ground up, we’re making direct use only of facts we have discovered for ourselves (though mentioning others along the way), deciding on our own abbreviations and terminology (occasionally allowing some orthodox terminology to tag along), and drawing all of our pictures by hand. But against that background, how can we possibly hope to picture these new beasts that we’ve unwittingly conjured up? We have no idea at this point how to calculate a specific number for quantities like or , so how on earth are we supposed to visualize something like the graph of or ? Though our powers of visualization are limited in this new part of our universe, this lack of visual acuity need not stand in the way of our getting a visceral feel for the behavior of these new machines. Let’s spend a moment using what we know in order to get an idea of what some of these machines look like. Rather than trying to picture arbitrarily complicated machines like

M(x) ≡ x^−1/7 + 92x^21/5 − (x^−3/2 + x^3/2)^333/222

let’s instead focus on the simplest representatives of the new machines we’ve created. In the previous interlude, we invented three new types of powers: zero, negative, and fractional. Since zero powers just turned out to be 1, we really only have two genuinely new phenomena to deal with: negative powers and fractional powers. The simplest representative of negative powers seems to be

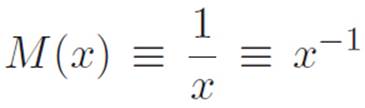
while the simplest representative for fractional powers seems to be

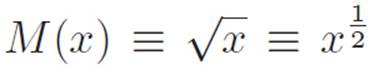
Let’s start with the first one. It doesn’t really matter that we don’t have the patience or even the knowledge to calculate a specific number for 7⁻¹ or (9.87654321)⁻¹ or anything else. All we want to know is the general, big-picture behavior of the machine M(x) ≡ x⁻¹, so that we can gain an intuitive feel for what it looks like and how it behaves. Basically everything we know about this machine can be summarized by the following four mathematical sentences, which are all really just one sentence expressed in different ways.¹

Note: In the past, we’ve used tiny to stand for an infinitely small number, but here it just stands for a regular old number like 0.000(bunch of zeros)0001. Similarly, huge is a just a regular number too, not an infinitely big one.

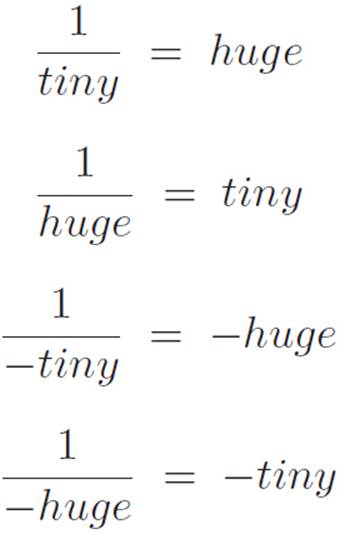
For example, 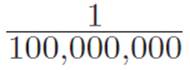is extremely tiny, while 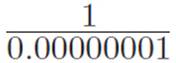is huge, and by making x smaller and smaller, we can make as huge as we want. We don’t need to do any tedious arithmetic to see this. It just follows from our view that there’s no such thing as division. Since the beginning, we’ve been saying that is just an abbreviation for , and the funny symbol is just an abbreviation for whichever number turns into 1 when we multiply it by b. Having defined this symbol not by what it is but by how it behaves, it follows naturally that 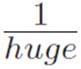should be a tiny number: 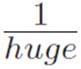stands for whichever number turns into 1 when we multiply it by huge, but if something only manages to get magnified to a size of 1 after we multiply it by a huge number, then the original number must have been fairly tiny. No arithmetic, just reasoning. As simple as this idea is, it’s the only idea we need in order to draw Figure 3.1.

Okay, so we still can’t compute a specific number for or , but getting a general understanding of for all values of x somehow wasn’t as hard as we expected. Mathematics can be strangely backwards like that. What about the other new type of machine? Can we figure out a way to visualize 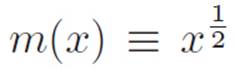, also known as ? Well, just as before, we have no idea how to compute a specific number for or or infinitely many other things. However! We do know how to do basic multiplication, so we know how to square whole numbers. For example,

and so on. Now, using the definition of fractional powers that we invented in the previous interlude, we can express all of the above sentences in a slightly different language:

What about numbers less than 1? Well, as a simple example, we know that 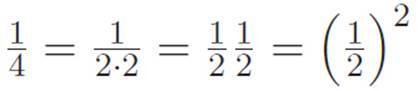, which is just another way of saying:

Figure 3.1: We know that (i) 1 over a tiny number is a huge number, (ii) 1 over a huge number is a tiny number, and (iii) in the two previous phrases, the meaning of “tiny” can be made as tiny as we want, for huge enough values of “huge,” and vice versa. This lets us build a general understanding of what the machine looks like, even though we are completely incapable of computing a specific number for quantities like , as well as largely uninterested in doing so.

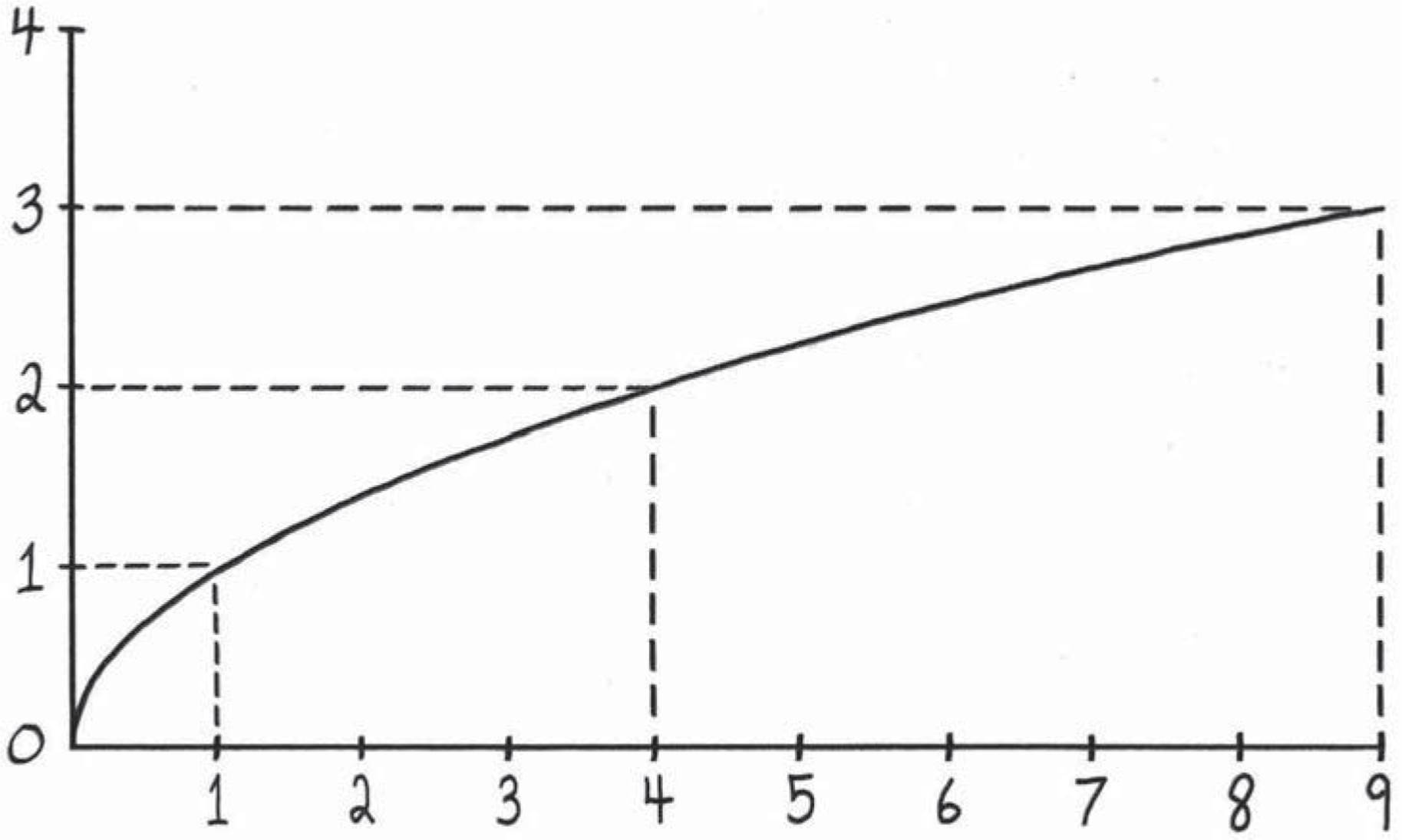
Figure 3.2: Using what little we know to picture the one-half-power machine .

So whereas taking the power of a number bigger than 1 makes it smaller, taking the power of a number smaller than 1 seems to make it bigger. Using everything we just wrote down, we can build a reasonably detailed picture of what the machine 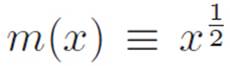looks like. Our attempt is shown in Figure 3.2. Just as before, we managed to develop a general feel for the machine’s behavior for all values of x, even though we still have no idea how to compute a specific number for arbitrary quantities like . In all of mathematics, contrary to what we are led to believe, this is the norm.

3.1.3Playing with Our Accidents and Getting Hopelessly Stuck

We have a habit in writing articles published in scientific journals to make the work as finished as possible, to cover all the tracks, to not worry about the blind alleys or to describe how you had the wrong idea first, and so on. So there isn’t any place to publish, in a dignified manner, what you actually did in order to get to do the work, although, there has been in these days, some interest in this kind of thing.

—Richard Feynman, Nobel Prize Lecture, December 11, 1965

Okay, let’s see if our magnifying glass idea continues to make sense when we use it on these new things. Let’s try it on the simplest of our new fractional power machines: 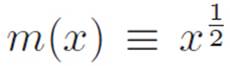. Here we go:

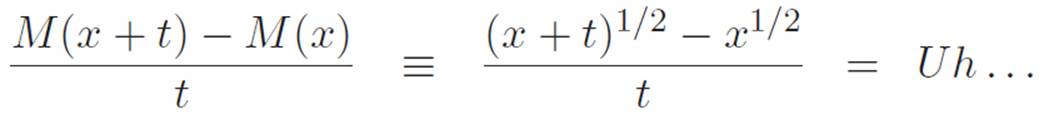
We have absolutely no idea what to do with this. Let’s give up on this one for a minute and see if our magnifying glass is any easier to use on one of those negative-power machines. Again, let’s try the simplest example: . Ready, set, go:

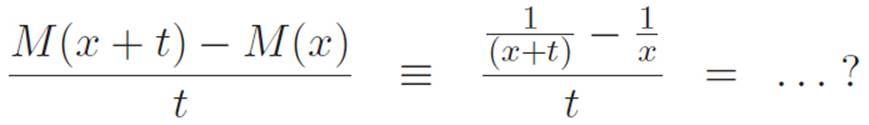
Stuck again. We have no clue what to do with any of these ugly new beasts. But despite our almost total lack of familiarity with them, we do know something about them. We invented them, after all! We generalized powers by saying “they’re anything that behaves this way,” where “behaves this way” meant “obeys the break-apart-the-powers formula.” Because of this, one of the fundamental properties of these unfamiliar new machines is that we can turn them into something more familiar by banging them into other machines with multiplication. For example, no matter what n is, we invented the fact that (xⁿ) (x⁻ⁿ) = xⁿ⁻ⁿ = x⁰ = 1, or more briefly:

Remember in the last chapter, we figured out that for any machines f and g (not necessarily plus-times machines, but possibly something much more exotic), it had to be the case that (f + g)′ = f′ + g′. That is, we found a way to talk about the derivative of two things added together in terms of the derivatives of the individual pieces (or to say the same thing differently, the derivative of a sum is the sum of the derivatives). We were surprised to find how easy it was to convince ourselves of this using only our definition of the derivative, even if we didn’t know anything at all about the particular individual personalities of f and g. We have no idea what the derivative of x⁻ⁿ is, but the above idea together with equation 3.1 suggests a promising approach.

If we could figure out how to talk about the derivative of two things multiplied together in terms of the derivatives of the individual pieces, then we might be able to ambush these new untamed machines by using equation 3.1 in two different ways. Let’s say we write down an abbreviation for what we can call a “trick machine.” It could be something like T(x) ≡ (xⁿ)(x⁻ⁿ). We’re using the letter T because we’re attempting to Trick the mathematics into telling us something. This machine T is js u t. . .

(The familiar rumbling noise is heard again. The intensity of the rumbling increases for several seconds and then immediately stops without warning.)

Ugh, not again! Stupid noise made me spell “just” wrong. Sorry, Reader, that must be one of those famous California earthquakes. Just ignore them if you can. I doubt they’ll turn out to be important. Where were we? Right! The trick machine T(x) ≡ (xⁿ) (x⁻ⁿ) is just a fancy way of writing the number 1, so we know that the derivative of T is zero.

However, if we had in our possession a way to talk about the derivative of a “product” (two things multiplied together) in terms of the derivatives of its pieces, then we could switch hats, think of the machine T as a product of the two machines xⁿ and x⁻ⁿ, and use this as-yet-undiscovered method of talking about the derivative of the whole thing in terms of its pieces. We would then have done the same thing in two ways. On the one hand, we know the derivative of T is zero, since the machine T is just the constant machine 1 in disguise. On the other hand, we’d have another way of expressing T’s derivative in terms of a thing we know (the derivative of xⁿ) and a thing we want to know (the derivative of x⁻ⁿ). Then, if we happened to get extremely lucky, we might be able to manipulate this complicated expression, and somehow isolate the piece that we wanted (namely, the derivative of x⁻ⁿ). It’s a total shot in the dark, and it probably won’t work, but at very least it’s a creative idea.

And hey! If we could find a general formula for the derivative of two things multiplied together, then we might be able to tackle the fractional power machines too! We completely failed on M(x) ≡ x^1/2 earlier, but because of the way we invented the idea of powers, we know that

So just like before, if we could somehow talk about the derivative of a product in terms of the individual derivatives, then we might be able to use the above expression to trick the mathematics into telling us what the derivative of x^1/2 is!

(As the section comes to an end,

no more rumbling is heard.

An unsettling silence

has fallen over

the book

. . .)

3.1.4A Shot in the Dark

This idea seems a bit far-fetched, and we’re not sure if it’ll work, but we may as well try. After all, there’s not much else to do, and there’s no one around to punish us if we fail. Let’s play around a bit and see if we can make any progress on this hopeful delusion of a problem.

Richard Feynman famously said that the first step in discovering a new physical law is to guess it. It was a joke, but he wasn’t really joking. Discovering new things is an inherently anarchic process. Reality doesn’t care how we stumble upon its secrets, and guessing is as good a method as any. Let’s take that approach. We already know that (f + g)′ = f′ + g′. That is, we know that the derivative of a sum is the sum of the derivatives. So, the first natural thing to guess is that maybe the derivative of a product is the product of the derivatives. Sounds reasonable, right? Let’s write it down, making sure to remind ourselves it’s just a guess:

Alright, we’ve got a guess. The above guess was inspired by another fact we know is true, namely, (f + g)′ = f′ + g′, so we’re not just guessing randomly. If our guess is really correct, though, it has to be consistent with what we already know, so let’s see if it reproduces things we discovered earlier. We know that the derivative of x² is 2x, and if the above guess is true, then we could also write the derivative of x² like this:

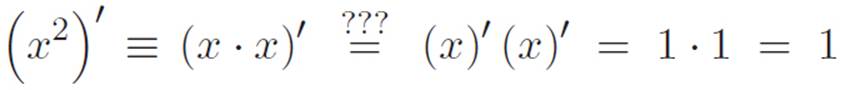
Well that didn’t work. It’s definitely not true that 2x is always equal to 1 no matter what x is. Oh well. Our guess was wrong, but I guess we learned something. And hey! In retrospect, we should have been able to see that our guess was wrong to begin with. After all, if it were true that (fg)′ = f′ g′, then the derivative of everything would be zero. Why? Well, any machine f is the same as 1 times itself, so if our guess had been true, then we could always just write this:

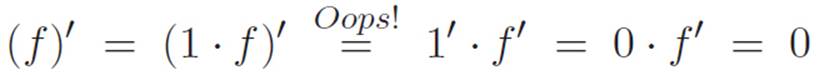
Now that our first guess failed, it’s not really clear what to do. I guess there’s not much we can do except go back to the drawing board. What was the drawing board? Well, I guess the definition of the derivative is as far back as we can go. Let’s just imagine that f and g are any machines, not necessarily plus-times machines, and then let’s define M(x) ≡ f(x)g(x). So M spits out the product of whatever f and g spit out. Then using the definition of the derivative, and using the abbreviation t to stand for a tiny number, we have

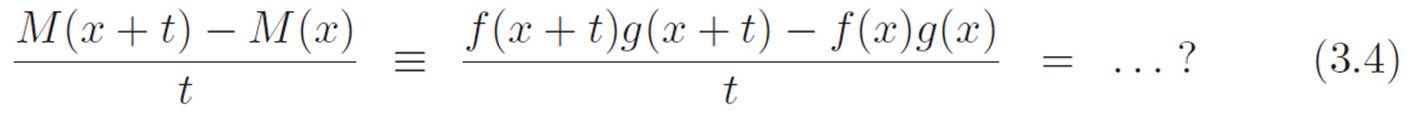
And we’re stuck again. That didn’t take long to unravel! What now?

Well, it would be nice if we could just lie and change the problem, because it almost looks like a problem we could deal with. I mean, if only that f(x + t) piece were really f(x) instead, then we might be able to make some progress. Let’s give up on the real problem for a moment and examine the version we’d get if we were allowed to lie. I’ll write at the spot where we change the problem. The symbol is where we’re lying in order to make the problem easier. That’s fine, as long as we remember that we’re not actually solving the original. This may turn out to be pointless, but who knows? Lying in order to make progress might give us some ideas of what to do on the problem that defeated us. Here we go:

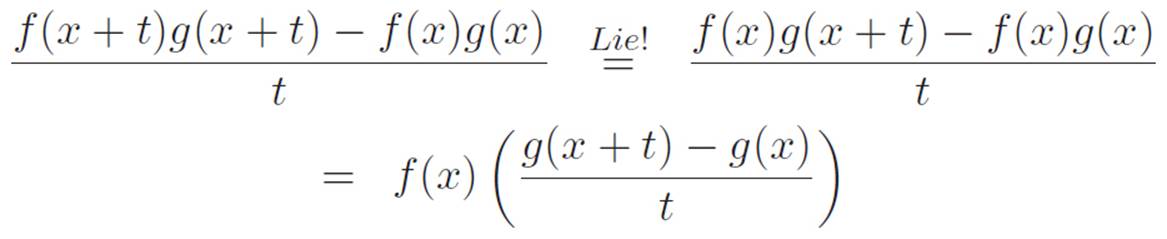
Nice! We already made it past where we got stuck before. Now turning t down to zero as usual makes the far right turn into f(x)g′(x), and the far left is just the derivative of M(x) ≡ f(x)g(x), so we get

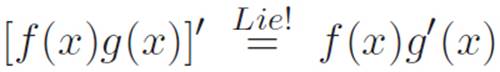
Does this help? Well, we got an answer, but it’s not the real answer, because we lied. But maybe if we go back to the original problem and perform the same lie, but then correct for the lie, then we’ll be able to make a similar kind of progress without changing the original problem. How do we lie and correct? Well, let’s add zero. . . but not just any zero. Instead of actually modifying the problem like we did above, let’s just add the piece we wish were there, and then subtract the exact same piece so that we don’t change the problem.

So sort of like before, the lie is to add f(x)g(x + t) to the top of the original problem, but now we’ll also have to subtract f(x)g(x + t) back off again, to avoid changing anything. The end result is that we’re doing nothing. We’re just adding zero. But saying “now add zero,” in the middle of a long string of equations doesn’t really express what we’re thinking, and it certainly doesn’t do justice to how strange and clever this idea is. Really, we’re just anarchically doing whatever we want, in order to make progress, and then apologizing for our recklessness by adding an equal and opposite antidote to undo whatever we did. This mixture of poison and antidote doesn’t change the problem, but the problem grows a kind of scar of the form “(stuff) − (stuff)” as a result of what we did, and if we constructed our lie carefully, this gives us something to grab on to in order to pull ourselves forward. Let’s see if this idea actually works. Ready? Here we go:

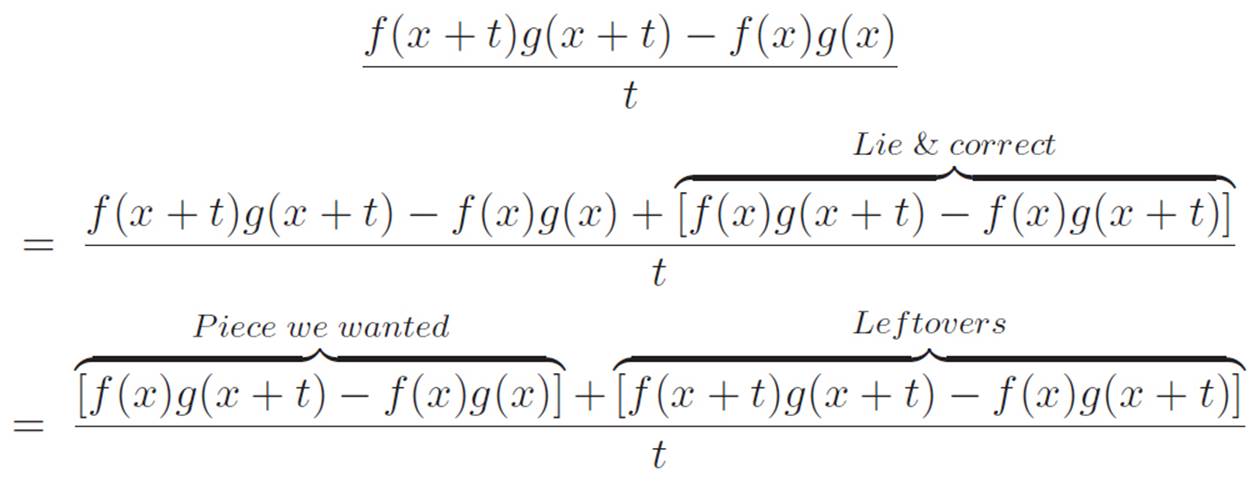
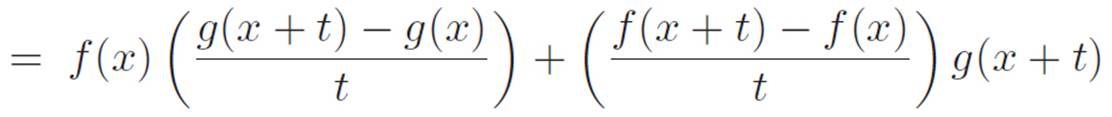
That worked out much better than we expected. In correcting for the lie, we ended up with some extra leftovers that we didn’t necessarily want. However, in a surprising stroke of luck, the same nice thing ended up happening with the leftovers as with the piece we wanted, because we found that we could peel off the g(x + t) piece and take it outside.

We’ve got four pieces in the last line of the equations above. Now, once we turn t down to zero, every one of these pieces will turn into either one of the two machines or one of their derivatives. The first piece will stay f(x), the second will morph into g′(x), the third will morph into f′(x), and the fourth will be g(x). So we’ll get f′(x)g(x) + f(x)g′(x). Our lying and correcting actually worked! Let’s celebrate and summarize by writing this in its own box:

How to Talk About the Derivative of a Product in Terms of the Pieces

We just discovered:

If M(x) ≡ f(x)g(x)

then M′(x) = f′(x)g(x) + f(x)g′(x)

Let’s say the exact same thing in a different way:

(fg)′ = f′g + g′f

Let’s say the exact same thing in a different way. . . again!

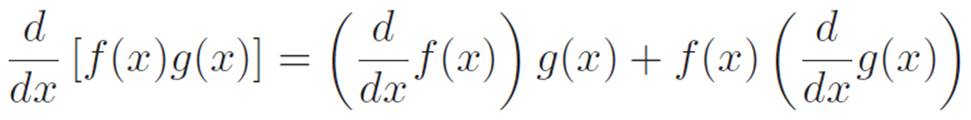
This is getting crazy, but let’s do it again!

[f(x)g(x)]′ = f′(x)g(x) + f(x)g′(x)

You still there? Okay, one more time!