Burn Math Class: And Reinvent Mathematics for Yourself (2016)

3. As If Summoned from the Void

3.2. !scitamehtaM eht gnikcirT

Having dramatically failed in our initial attempt to figure out the derivatives of our new ugly machines, we now return with a much more powerful hammer.² We still aren’t completely sure if this will work, but let’s try.

I’m choosing to use the word “hammer” for certain theorems, particularly the so-called “rules for differentiation.” The word “hammer” is appropriate because (i) they’re extremely powerful, (ii) they allow us to shatter hard problems into smaller pieces, and (iii) every use of the words “theorem” or “rule” only adds to the overall boredom of the universe.

Shh! Don’t let the mathematics hear us!

Now we can try to trick the mathematics into telling us how to differentiate our new unfamiliar machines, like we talked about earlier.

Let’s define the trick machine to be T(x) ≡ (xⁿ) (x⁻ⁿ).

We secretly know that T(x) is just the boring machine that always spits out 1.

That is, secretly, T(x) = 1 for any x.

So we know its derivative is T′(x) = 0.

But pretend we don’t know that!

Let’s act like we think it’s two complicated things stuck together,

and see what the mathematics tells us. . .

Ahem. Sorry, had to clear my throat there for a minute. Okay, mathematics, now we’re going to differentiate T(x). It’s a totally normal machine, I promise. The reader and I aren’t hiding anything from you. Earlier we figured out that the derivative of xⁿ is just nxⁿ⁻¹, so let’s use that fact together with the hammer we just invented.

Even though we know for sure that T′(x) = 0, let’s put question marks over the equals sign so that the mathematics doesn’t catch on to what we’re doing.

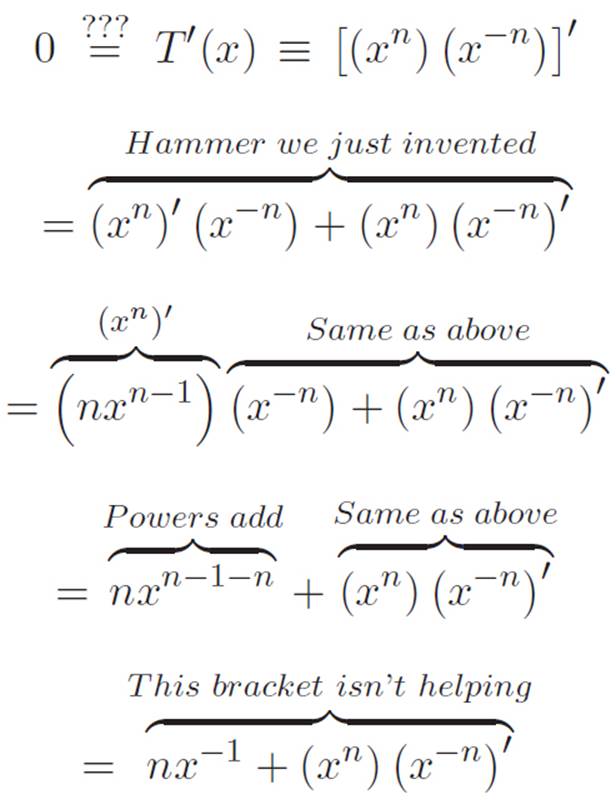
Okay. So if all of this really were equal to zero. . .

Shh! We know it is, but we don’t want the mathematics to catch on!

. . . then we could try to isolate (x⁻ⁿ)′ becau—

(Author is interrupted yet again, first by the familiar rumbling noise, and then by an unfamiliar voice.)

Mathematics:

(In a genuinely unsuspicious voice)

WHY ARE YOU TRYING TO DO THAT?

Oh, you know. . . just messing around. . . for fun. . .

Mathematics:

. . . CARRY ON.

Uhh. . . okay. I wasn’t expecting that to happen.

(Author sits in silence for a moment, uncertain about this unexpected new development. This could end up fundamentally changing the book. Important decisions would have to be made.)

Okay, forget it. . . I’ll just edit it out later. Anyway, so if it were really the case that T′(x) = 0, then we could pick up where we left off, and write:

0 = nx⁻¹ + (xⁿ) (x⁻ⁿ)′

We’re trying to isolate the piece we don’t know, which is the (x⁻ⁿ)′. First we can do this,

−nx⁻¹ = (xⁿ) (x⁻ⁿ)′

and then this,

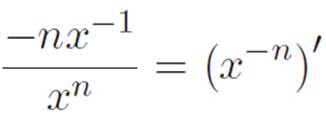
Or to rewrite the same thing in the language of negative powers:

(x⁻ⁿ)′ = −nx⁻ⁿ⁻¹

Nice! Check out what we just did. We tricked the mathematics into telling us the derivative of the unfamiliar machine x⁻ⁿ by feeding it a trick machine T(x) ≡ (xⁿ) (x⁻ⁿ). We called it a “trick machine” because it was really just the number 1 in disguise, but we pretended we didn’t know that in order to get a second expression for its derivative. We got this second expression by thinking of the machine as the product of two other machines: a familiar one that we knew how to differentiate, and an unfamiliar one that we wanted to figure out how to differentiate. This gave us a bunch of stuff that added up to zero, and then we just isolated the piece we wanted. Feels like cheating, but it’s not! If our hammer (fg)′ = f′g + g′f is really true (which we know it is because we invented it), then our tricky way of using that hammer has to have given us the right answer too. Hah! Take that, mathematics!

Mathematics:

(In a booming but quiet and slightly hurt voice)

I DON’T MEAN TO INVITE MYSELF INTO THIS CONVERSATION, YOU TWO, BUT I KEEP OVERHEARING YOU SAY THAT YOU’VE TRICKED ME. I SUPPOSE IT’S NOT ESSENTIAL, BUT IF YOU’LL ALLOW ME A MOMENT, I COULD DEMONSTRATE — OR ATTEMPT TO, ANYWAY — THAT THIS STYLE OF REASONING IS IN NO WAY A(MISLEADING TRICK) OR (TABOO).³ ASSUMING THAT YOU GRANT ME THE TIME AND THAT YOU FIND YOURSELVES CONVINCED, WOULD YOU PLEASE STOP SAYING YOU’VE TRICKED ME?

Mathematics: APOLOGIES FOR THE PARENTHESES, YOU TWO, BUT THE SENTENCE WAS NON-ASSOCIATIVE AND THUS UNDEFINED (WITHOUT THE FIRST PAIR), AND AESTHETICALLY UNPLEASING (WITHOUT THE SECOND). I’LL OMIT THEM WHEN I CAN, BUT IT IS IMPORTANT TO MAKE ONESELF CLEAR, OR RATHER (TO SAY THE SAME THING LESS PRESCRIPTIVELY) I WOULD LIKE TO MAKE MYSELF UNDERSTOOD. UNDERSTAND?

Author: Uhh. . . sure.

Reader: No problem.

Reader: (Quietly) What’s going on?

Author: I don’t know! This has never happened before.

Reader: I’m not sure how I feel about this.

Author: Me neither! Since when can mathematics talk!?

Reader: You tell me! You’re the one who’s writ—

Mathematics:

MIND IF I INTERRUPT?

Reader: Go ahead.

Author: I guess.

Mathematics:

OKAY, I’M NOT ENTIRELY SURE WHAT’S GOING ON EITHER. I HAD JUST WOKEN UP IN THE VOID WHEN I HEARD SOMEONE SAYING THEY’D TRICKED ME. I. . . I DIDN’T MEAN TO INTERRUPT WHAT YOU WERE DOING. . . BUT ONE CAN ONLY LISTEN TO OTHERS TALKING ABOUT ONESELF FOR SO LONG BEFORE ONE STARTS TO FEEL. . . ALONE. . . OR A FEELING THAT’S ISO- OR PERHAPS HOMOMORPHIC. . . SPEAKING OF WHICH, YOU TWO WEREN’T FOOLING ANYONE WITH THE NAME OF THIS SECTION. YOU THINK I CAN’T SEE THROUGH SUCH A TRIVIAL ISOMORPHISM?

Reader: What’s an isomor—

Author: Later. Now’s not the time.

Mathematics:

BEFORE I CONTINUE, LET ME CREATE A NEW SECTION. IF OUR DISCUSSION IS TO CONTINUE, IT SHOULD DO SO UNDER A BANNER THAT MORE ACCURATELY REFLECTS THE REALITY OF THE SITUATION. . .⁴

(Narrator: As the new section begins, Author decides to format the dialogues more sensibly, and in a way that takes up less space. “After all,” Author thought, “who knows how many more of these there might be?”)