Burn Math Class: And Reinvent Mathematics for Yourself (2016)

3. As If Summoned from the Void

3.5. A Phase Transition in the Creation Story

Principium cuius hinc nobis exordia sumet,

nullam rem e nihilo gigni divinitus umquam.

(But only Nature’s aspect and her law,

Which, teaching us, hath this exordium:

Nothing from nothing ever yet was born.)

—Lucretius, De Rerum Natura (On the Nature of Things)

After all the mathematical dust settled, we found that same familiar pattern staring us in the face yet again. Having repeatedly repeated how we’re making all this stuff up ourselves, we’ve arrived at a juncture where we are suddenly less confident of this assertion. It is time to step back for a moment and reconsider our premises. What exactly is the nature of mathematics and mathematical truth? Despite the fact that our universe consists entirely of things we’ve invented ourselves, we increasingly appear to be discovering truths that exist independently of us. We invented the idea of machines, we invented powers, we invented slope, we invented the infinite magnifying glass, and we invented the idea of the derivative, but we didn’t intentionally force the mathematics to obey this simple pattern that keeps showing up whenever we differentiate x^#. Somehow we keep rediscovering the fact that (x^#)′ = #x^#−1 for different types of numbers, even though different types of numbers required us to make wildly different arguments in order to arrive at the same pattern. We found this pattern for positive whole numbers, then for negative whole numbers, then for any power that looks like 1 over a whole number, and now for any number that can be written as one whole number divided by another, yet we asked for exactly none of these facts.

We are indeed inventing everything ourselves, and as such, anything that is true about the world we’re inventing must be true as a consequence of some assumption we’ve made along the way, but we’ve now begun stumbling headlong into facts that bear no resemblance to any assumption we’ve explicitly made. This type of thing happens endlessly in mathematics, and the odd feeling caused by such discoveries was well expressed in the following quote by Heinrich Hertz:

One cannot escape the feeling that these mathematical formulas have an independent existence and an intelligence of their own, that they are wiser than we are, wiser even than their discoverers.

You may think that only a crazy person would anthropomorphize mathematics like this, and I certainly can’t argue with that. But Hertz wasn’t crazy, and his quote illustrates an important point about the process of mathematical discovery. In this chapter and in Chapter 2, each time we rediscovered the “bring down the powers” pattern in the derivative of x^# for different types of numbers, we were witnessing firsthand the phenomenon Hertz described. We have thus arrived at a phase transition in our mathematical creation story. At this point, we have invented enough of mathematics — or rather, Mathematics — that it seems for the first time to exist independently of us, with its own moods, whims, and ideas. This chapter is just the first of many encounters with that Hertzian feeling. If such anthropomorphism counts as insanity, then so much the worse for sanity.

3.5.1Let’s Talk About What We Just Did

Let’s summarize the tools we’ve invented so far that let us deal with general machines, not necessarily plus-times machines, and let’s give them some names.

Hammer for Addition

(f + g)′ = f′ + g′

Hammer for Multiplication

(fg)′ = f′g + fg′

Hammer for Reabbreviation

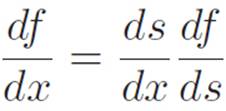
We also extended our hammers for addition and multiplication to versions that apply for n machines. However, these more general hammers are a bit uglier to write, and in practice we can usually just use the versions for two machines, so we’ve listed them here in their simplest forms.

These three hammers have names in the conventional textbooks. The hammer for addition is called the “sum rule,” and the hammer for multiplication is called the “product rule.” These are perfectly well-chosen names, since they remind us of what we’re talking about, although the term “rule” can have the effect of misleading people about the nature of mathematics (and I stand by the assertion that every use of the term “rule” simply adds to the overall boredom of the universe).

However, while that’s just a minor quibble about terminology, the standard way of presenting the third hammer is problematic enough that it deserves its own section. Let’s jump into that section now.