Burn Math Class: And Reinvent Mathematics for Yourself (2016)

3. As If Summoned from the Void

3.6. Hammers and Chains

The hammer for reabbreviation is usually called the “chain rule.” While this name is not so bad, the notation that most books use to talk about it is so bizarre that it needlessly tortures students and deeply obscures the underlying simplicity of the idea. Remember that one of the main hurdles in our invention of the hammer for reabbreviation (the “chain rule”) was to realize that the idea did not play nicely with the prime notation. It is not impossible to use the prime notation, but we found that it was extremely easy to make mistakes, since we’re really interpreting x as the variable in one half of the problem, and interpreting s (stands for stuff) as the variable in the other half of the problem. Here’s how textbooks usually present the idea.

How Textbooks Talk About the Hammer for Reabbreviation

The “chain rule” is a rule for differentiating the composition of two functions. That is, whenever h(x) = f(g(x)), the chain rule says that h′(x) = f′(g(x)) g′(x).

To be clear, this textbook-y way of talking about the “chain rule” is not incorrect; it’s just an unnecessarily complicated way to explain such a simple idea. Further, while it’s true that the “chain rule” can be interpreted as a statement about differentiating a composition of two functions, phrasing the idea this way fails to convey a crucial point: what counts as a “composition of two functions” is completely up to us! We can think of a function like M(x) ≡ 8x⁴ as a “composition of functions” (that is, one function plugged into another) in tons of different ways. For example, if we define f(x) ≡ x⁴and g(x) ≡ 8x, then M(x) = g(f(x)). Alternatively, if we define 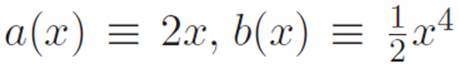, then M(x) = b(a(x)). There are infinitely many ways of thinking of any function as the “composition” of two or three or fifty-nine other functions. In that sense, there’s no objective sense in which we can say that a particular machine is “the composition of two functions.” It’s always up to us whether we want to think of it that way. Why would we want to? Well, we wouldn’t. . . unless it helps us! After all, that was the thought process that led us to invent the hammer for reabbreviation in the first place.

To see the difference between these two ways of thinking in more detail, we’ll use the hammer for reabbreviation (the chain rule) to find the derivative of M(x) ≡ (x¹⁷ + 2x + 30)⁵⁰⁹ using the methods common in textbooks, and contrast them with the method we used above. We’ll show lots of steps to illustrate the ideas, even though this problem could be solved with either method in one step, once we’ve mastered the idea.

How Textbooks Usually Use the Hammer for Reabbreviation (“Chain Rule”)

We want to differentiate the function

M(x) = (x¹⁷ + 2x + 30)⁵⁰⁹

Defining the functions

f(x) = x⁵⁰⁹

and

g(x) = x¹⁷ + 2x + 30

we find that M is a composition of functions:

M(x) = f(g(x))

Differentiating f, we obtain

f′(x) = 509x⁵⁰⁸

Similarly, differentiating g, we find

g′(x) = 17x¹⁶ + 2

Therefore, applying the chain rule gives

M′(x) = f′(g(x))g′(x) = 509 (x¹⁷ + 2x + 30)⁵⁰⁸ (17x¹⁶ + 2)

How We’ll Usually Use the Hammer for Reabbreviation (“Chain Rule”)

We want to differentiate the machine

M(x) ≡ (x¹⁷ + 2x + 30)⁵⁰⁹

thinking of x as the variable.

This is an ugly problem, but it’s just a bunch of stuff to a power, which is something we’re less scared of, so let’s abbreviate

s ≡ x¹⁷ + 2x + 30

where s stands for stuff. Then

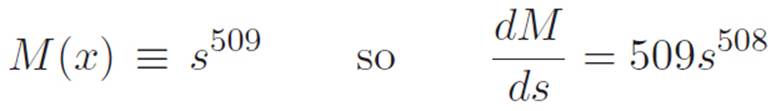
But we wan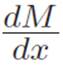t , not 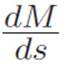, so lying and correcting for the lie gives

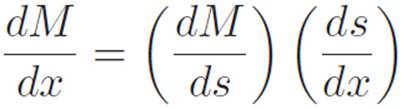
Lying and correcting for the lie tells us that we still need the derivative of (stuff), thinking of x as the variable. But this is easy too.

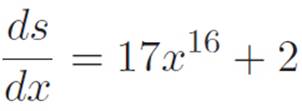
So finally, we have

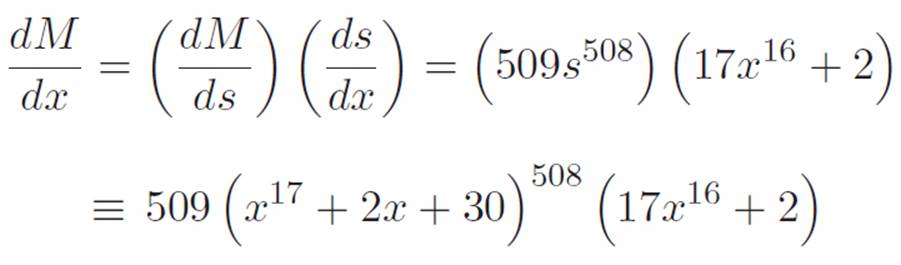
Notice that in both cases we get exactly the same answer. These two ways of doing things are logically equivalent, but they are most certainly not psychologically equivalent. Worse, calling it a “rule for differentiating compositions of functions” gives people the idea that there is something called a “composite function.” There isn’t.

This “only if it helps us” philosophy was the reason we invented all three of our hammers in the first place, and it is another reason we’re using the word “hammer” rather than “rule” or “theorem” to describe optional methods of shattering hard problems into simpler pieces. The terms “sum rule,” “product rule,” and “chain rule” aren’t incorrect, but they’re subtly misleading. These three shattering methods are not rules telling us what to do, but tools telling us what we’re free to do, if we want to. This is an extremely important distinction, so let’s give it its own box:

The Point of All the Hammers

1.We can choose to think of any particular machine as “really” being two machines added together, but only if it helps us.

This is why we invented the hammer for addition.

2.We can choose to think of any particular machine as “really” being two machines multiplied together, but only if it helps us.

This is why we invented the hammer for multiplication.

3.We can choose to think of any particular machine as “really” being one machine eating another, but only if it helps us.

This is why we invented the hammer for reabbreviation.

Having made this point loud and clear, let’s add these three hammers to our quickly growing arsenal, and continue the journey.