Burn Math Class: And Reinvent Mathematics for Yourself (2016)

4. On Circles and Giving Up

4.3. Equivalences of Our Ignorances

Reader: Here’s the idea:

1.A really thin rectangle kind of looks like a line.

2.The area of a rectangle comes from multiplying the two side lengths.

Our give-up number lets us write the area of a circle like this:

even though we don’t know what that number # is. So let’s imagine two circles, one with radius r, and the other with radius r + t, where t is some really tiny number. We make the second circle by expanding the first one a tiny amount, so imagine one circle inside the other. We’ve been writing , but now we need abbreviations for two different circles, so let’s write A(r) for the area of the inside one, and A(r + t) for the area of the outside one. So the whole thing looks like an extremely thin donut. I’ll draw it in Figure 4.3. The thin donut’s area should be:

A_donut = A_outer − A_inner ≡ A(r + t) − A(r)

Our sentence A(r) = # · r² still has a number we don’t know inside it, but let’s use it anyway. It tells us that

A_donut = # · (r + t)² − # · r²

Figure 4.3: For infinitely thin donuts, we might be able to compute the area as if it were a thin rectangle. In the picture above, we’re imagining that the inner circle has a radius of r, and the outer circle has a radius of r + t, where t stands for some really tiny number. So the thickness of the donut is whatever that tiny number t is.

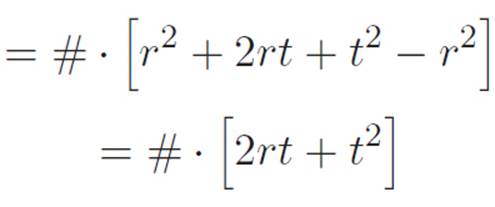
So this is the area of the thin donut. But there’s another way to think about it. If we zoom in really closely on any part of a circle, it’ll look like a straight line. So if we zoom in on any tiny part of our thin donut, it’ll look like a long thin rectangle, right?

Mathematics: SURE.

Author: Sure.

Reader: Now stay with me here. If we make the donut thin enough, then we can imagine cutting it with scissors and “unfolding” it to make a long thin rectangle. Then we just hope that we can compute its area as if it were a rectangle, without being too wrong, like this:

Area of thin donut = (long length) · (thin width) = (Distance around circle) · (t)

Mathematics: WAIT, YOU JUST WROTE “DISTANCE AROUND CIRCLE.” THAT’S WHAT MY GIVE-UP NUMBER IS TALKING ABOUT. LOOK:

SO I CAN HELP YOU OUT. I’LL REPLACE THE WORDS “DISTANCE AROUND CIRCLE” WITH MY GIVE-UP EXPRESSION TO TURN YOURS INTO

Author: Hey, we described the same thing twice. A minute ago we wrote

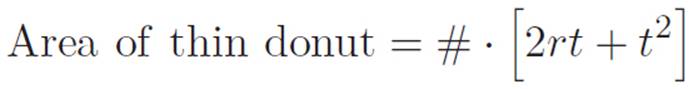
Mathematics: OH WAIT, I USED A DIFFERENT ABBREVIATION THAN YOU DID, BUT THE THING I CALLED d IS JUST TWICE AS BIG AS WHAT YOU CALLED r. LET ME REPLACE MY d WITH 2r AND COMBINE ALL THIS:

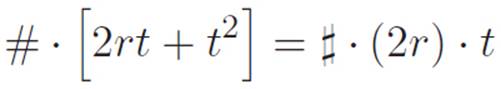
Reader: There’s at least one t attached to everything.

Author: Oh right. That’s because both sides are talking about the area of the thin donut, and its area gets smaller and smaller as we shrink the tiny number t, so it makes sense that everything has at least one t attached. But we’re just trying to compare our two give-up numbers, so let’s cancel one of the t’s from both sides and rewrite it this way:

What’s that t doing there?

Reader: Oh! I guess that’s the leftovers. I was just arguing that we can almost think of the thin donut’s area as “length times width.” It won’t be exactly right to do that, but it becomes more and more reasonable to think that way as the donut gets thinner. Seems like it should be exactly right when the donut is infinitely thin. So maybe we should really turn that t piece all the way down to zero. If we turned it down to zero without first canceling it from both sides, we would have gotten 0 = 0. That’s still right, it’s just not helpful. But now turning it down to zero gives

and now we can kill-off 2r from both sides to get

Author: So our give-up number is the same as his give-up number?

Mathematics: HIS? I DON’T BELIEVE I HAVE A GENDER, AUTHOR.

Author: Oh, of course. Sorry. Pronouns are tricky.

Reader: Anyways, the two give-up numbers are the same.

Author: But we still don’t know either of these numbers! Or rather, this number. Sorry. Pluralization is tricky.

Mathematics: DOES IT MATTER THAT WE DON’T KNOW WHAT NUMBER IT IS?

Author: No, not really. It’s just strange that we can be completely unaware of what numbers # and are to begin with, and then somehow show that they’re the same.

Mathematics: I DON’T SEE WHAT’S SO STRANGE ABOUT THAT. AND CAN WE JUST CALL THIS NUMBER FROM NOW ON? WE MAY WANT TO USE # FOR OTHER THINGS.

Author: Sure.

Mathematics: FANTASTIC. SO NOW WE KNOW:

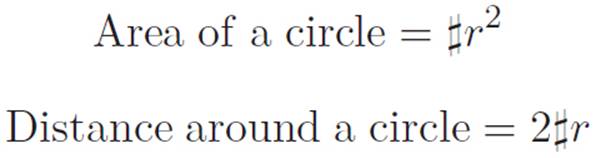
BUT WE DON’T KNOW WHAT IS.

Author: So the derivative of a circle’s area with respect to its radius is its circumference?

Mathematics: WELL, I SUPPOSE IF YOU WANT TO SOUND LIKE A TEXTBOOK.

)¹

(Narrator: It was especially inconsiderate to interrupt Narrator, Narrator thought, since Narrator’s narration (or rather, metacommentary) takes place within parentheses and, as such, any unanticipated interruption is liable to cause difficult-to-detect errors in syntax and/or problems parsing (t/T)he (b/B)ook (/later), respectively. But I digress. . .)