Burn Math Class: And Reinvent Mathematics for Yourself (2016)
Act II
5. Aesthetics and the Immovable Object
Interlude 5: Two Clouds
No More Mysteries?
In 1894, the famous physicist Albert Michelson remarked that all of the fundamental mysteries of physics appeared to have been resolved. The physics of the future, therefore, would be primarily concerned with cleaning up a few details. Michelson is quoted as saying:
The more important fundamental laws and facts of physical science have all been discovered, and these are now so firmly established that the possibility of their ever being supplanted in consequence of new discoveries is exceedingly remote. . . [O]ur future discoveries must be looked for in the sixth place of decimals.
Six years later, a similar remark was made by William Thomson, more commonly known as Lord Kelvin. As he put it:
The beauty and clearness of the dynamical theory, which asserts heat and light to be modes of motion, is at present obscured by two clouds. I. The first came into existence with the undulatory theory of light, and was dealt with by Fresnel and Dr. Thomas Young; it involved the question, how could the earth move through an elastic solid, such as essentially is the luminiferous ether? II. The second is the Maxwell-Boltzmann doctrine regarding the partition of energy.
Kelvin’s two clouds turned out to be far more than technical details of minor interest; they now comprise the two fundamental pillars of our modern understanding of Nature. The first mystery was only resolved with the advent of Einstein’s theory of special relativity, while the resolution of the second mystery led to the even more mysterious framework of quantum mechanics. Although these two theories can be combined in what is commonly known as quantum field theory, Einstein’s theory of general relativity still does not “play nicely” with quantum mechanics, and one of the main unsolved mysteries in physics to this day is how to combine the two in a successful quantum theory of gravity. More than a hundred years after the remarks of Michelson and Kelvin, many mysteries remain in our understanding of the universe. A glance at history shows that the remarks of Kelvin and Michelson are simply a special case of a quite general phenomenon: a recurrent human fondness for the always misguided idea that everything has been discovered, everything has been done, everywhere has been explored. The catalog includes:
Everything that can be invented has been invented.
—Charles H. Duell, Commissioner, U.S. Patent Office, 18992
This “quote” is actually one of those persistent apocryphal misquotations. Such quotes exist in a strange state between fiction and nonfiction, and have evolved methods of self-replication without the need of a primary source. Although there must have been a first time this quote was uttered, it appears to have no connection with the U.S. Patent Office or any of its commissioners, but rather appears to have been first uttered in a spaceless, timeless Void. Needless to say, even if this speculation were true, it would be equally difficult to find a primary source.
We are probably nearing the limit of all we can know about astronomy.
—Simon Newcomb, early American astronomer
Inventions reached their limit long ago and I see no hope for further development.
—Julius Sextus Frontinus, prominent Roman engineer (ca 40–103 AD)
What has been will be again,
what has been done will be done again;
there is nothing new under the sun.
—Ecclesiastes 1:9
In every case, declarations to the effect that “everything about X is known,” have turned out to be dramatically wrong. Such presump—
(Author looks up from his computer.)
Author: Hey, do either of you know how to spell “presumptuous”?
Reader: Why?
Author: For a book I’m writing.
Mathematics: WHAT’S A BOOK?
Author: Nevermind.
The Scene
The three characters are sitting in Mathematics’s house, (number ∅ Void St., in the upper west Void).
The characters are bored and attempting to kill time.
Unbeknownst to any of them, they are failing in this effort, due to the timeless nature of the Void.
Reader is sitting in a undefined location, reading about Reader.
Author is procrastinating from work, by writing a book.
Mathematics is perusing this week’s edition of
The Entirely Blank Newspaper of the Void, featuring a lengthy commentary on a portrait of the sheet music for John Cage′s 4′33″, as painted by Robert 
(Ryman+Rauschenberg).
Author: There’s nothing to do.
Mathematics: OF COURSE THERE’S NOTHING TO DO. WHERE DO YOU THINK YOU ARE?
Author: No, that’s not the problem. We did everything already. Everything that can be invented has been invented.
Reader: How do you know?
Author: Well, can you think of anything we haven’t done yet?
Reader: Sure. We still didn’t figure out how to calculate 
.
Author: Yeah, yeah. But that’s just a technical detail. All that’s left to do is calculate to more and more decimal places. What’s the point?
Reader: Wait a second. . .
(Our characters wait for an undefined amount of time.)
Author: . . . Has it been a second yet?
Reader: I don’t know! We’re in the Void! Time is almost mostly nonexistent here. In any case, I didn’t literally mean “Wait one second.” I just meant that you shouldn’t be so ready to assume we’ve done everything.
Author: Well, can you think of anything big and important that we don’t know yet?
Reader: How am I supposed to know what we don’t know? If I knew that, wouldn’t I know it?
Author: Not necessarily.
(Reader thinks for a moment.)
Reader: Oh, I guess you’re right. Well, why didn’t we calculate yet?
Author: We don’t know how.
Reader: Why don’t we know how?
Author: Because we couldn’t figure out the areas of curvy things.
Mathematics: AND CURVY LENGTHS. WE COULDN’T DEAL WITH THOSE EITHER.
Author: Okay, I guess there are still two things we don’t know. Once we figure those things out, I guess we’ll know everythi—
(A bright flash of light fills the room.)
Mathematics: OH! THAT’S THE DOORBELL.
Reader: Why do you have a light for a doorbell?
Mathematics: NORMAL DOORBELLS DON’T WORK HERE. YOU SEE, THERE’S NO AIR IN THE VOID, SO THERE’S NOTHING FOR THE SOUND TO PROPAGATE THROUGH. FOR AWHILE NOBODY BOTHERED TO MARKET LIGHT-BASED DOORBELLS HERE, BECAUSE THEY ASSUMED THAT LIGHT WAS LIKE SOUND, IN THAT IT NEEDED A MEDIUM TO PROPAGATE THROUGH — AN “ETHER” IF YOU WILL. THIS SUBSTANCE WAS ASSUMED TO FILL UP OUTER SPACE, BUT OF COURSE EVERYONE KNEW THAT THERE’D BE NO ETHER HERE IN THE VOID, BECAUSE THE VOID IS THE VOID. THEN, AN UNKNOWABLE AMOUNT OF TIME AGO, A CLEVER FELLOW REALIZED THAT THERE IS NO SUCH MEDIUM — LIGHT CAN PASS DIRECTLY THROUGH EMPTINESS! FORTUNATELY, THIS FELLOW ALSO WORKED AT THE PATENT OFFICE, SO HE PATENTED THESE LIGHT-BASED DOORBELLS, AND IT IS NOW MUCH EASIER FOR WE VOID DWELLERS TO TELL WHEN SOMEONE IS AT THE DOOR.
(At this point, the three characters have been waffling about doorbells for an undefined amount of time since the doorbell flashed. Despite Mathematics’s claim that it is now much easier for Void dwellers to tell when someone is at the door, the three characters have completely forgotten about their patiently waiting guest.)
Author: Alright, where were we?
(The doorbell flashes again.)
Mathematics: OH! THAT’S THE DOORBELL.
Reader: Why do you have a light for a doorbell?
Mathematics: NORMAL DOORBELLS DON’T WORK HERE. YOU SEE, THERE’S NO AIR IN THE VOID, SO. . .
Author: No no no, we did this already.
(Mathematics reads through the above discussion.)
Mathematics: OH MY. . . INDEED WE DID.
Reader: Time is strange here.
Mathematics: WHO COULD POSSIBLY BE AT THE DOOR?
Author: How should I know?
(Author runs to the door, followed by Reader and Mathematics.)
Intralude: Introduction to Meta and Steve
(The door opens to reveal a cheery bald man. Author’s eyes widen.)
Author: Oh my Gö—
Stephen Kleene: Hello! I’m here about the foundations. Nature called and told me you were having some problems.
Author: (Starstruck) Nice to meet you! I’m Author. Let me introduce you to my friends. This is Reader, and this is Mathematics.
Mathematics: HELLO THERE.
Reader: Nice to meet you, Stephen.
Stephen Kleene: It’s wonderful to meet you two as well. And call me Steve. As long as we’re on the topic of introductions, I’ve got one of my own. It’ll be a moment. It’s parking the car.
(A deep blue van parks outside with undue precision. Austere white letters on the side of the van read: Kleene’s (Foundations) & (Conceptual Cleaning) Service. Est. 1952. Kleeneliness is next to Gödeliness. Eventually something exits the van and approaches the door.)
Stephen Kleene: Ah, fantastic. Author, Reader, Math, allow me to provide you with an introduction to my friend and business associate, Metamathematics.
Metamathematics: . . .
Stephen Kleene: Please, introduce yourselves to it.
Author: Hi.
Reader: Hello.
Metamathematics: . . .
Stephen Kleene: It’s not very talkative, but it doesn’t mean to be impolite.
Mathematics: CAN YOU TELL IT TO STOP STARING AT ME?
Stephen Kleene: (Chuckles) I’m afraid not, my friend.
(Metamathematics stares with a curious but expressionless face at Mathematics. Mathematics leers back, half mockingly, half out of uncertainty about what to do in this uncomfortable new situation.)
Stephen Kleene: My business associate will need some time to examine the foundations. In the meantime, I was thinking the three of us could go out for some drinks.
Reader: There are bars in the Void?
Stephen Kleene: Just one. Meta and I were hired to clean it up recently, and I’ve grown rather fond of the place. It’s called The Beweis Bar.
Author: I could go for some drinks.
Stephen Kleene: Oh dear. . . well. . . how to put this?. . . It’s a fairly formal place, friends. You three might want to change clothes.
Mathematics: I DON’T BELIEVE I OWN ANY CLOTHES.
Stephen Kleene: Oh. Of course. Well, at least wear this.
(Steve hands Mathematics a small pin shaped like the letter A.)
Mathematics: EXPLAIN, PLEASE?
Author: Just put it on so we can go. Reader and I already changed.
Mathematics: WHEN DID YOU—
Reader: The Void is timeless.
Author: Haven’t we been over this?
Mathematics: . . .
(Mathematics λ·reluctantly affixes the pin on itself, roughly where a lapel would go if it had one, where λ ∈ [0, 1].)
Stephen Kleene: You’re wearing it upside down. . .
(Mathematics smiles in (1 − λ)·amusement at Kleene, and rotates the pin by an angle of , where is defined as in Chapter 4, and λ is the same as before.)
Stephen Kleene: Alright. Stand back, everyone. Meta, do your thing.
Metamathematics: 
:
SubIntralude: The Beweis Bar
(Author, Reader, Mathematics, and Steve suddenly find themselves seated in a small building. The menu reads “The Beweis Bar. Formal attire required. Every night is |= ∧¬
night.”)
Stephen Kleene: Fantastic. Here we are. Waitress!
Waitress: May I take your orders?
Stephen Kleene: I’ll have the usual.
Waitress: Mahlo cocktails it is.
Author: I’ll have the Hahn-Banach and tonic.
Waitress: Separable or Unseparable?
Author: Separable, please. Don’t want to drink too much while I’m writing.
Waitress: (To Mathematics) And you?
Mathematics: WHAT’S THE PAN MATHEMATIC GARGLE BLASTER?
Waitress: One of our top sellers. Our spin on an old favorite.
Mathematics: I’LL HAVE ONE OF THOSE.
Reader: I can’t see the menu. . . what would you recommend?
Waitress: Since you’re new here, I’d start with the WKL0 shots. They’re fairly weak.
Reader: What are they?
Waitress: That’s a tough question. It’s not really clear what the WKL0 shots are. You see, our drinks are only defined up to isomorphism — it’s basically the Void’s only law.
Reader: What’s an isomorphism?
Waitress: Basically just a meaningless change of abbreviations. Two things are isomorphic if they have all the same behaviors, even though they might look different. If two things are indistinguishable when you just look at how they behave, then they’re really the same thing as far as the Void is concerned, and we’re not allowed to treat them differently. It’s Void policy.
Reader: Uhh, can you give me an example?
Waitress: 
Reader: What? How is that an example? You just said “Sure. How’s this for an example?”
Waitress: Precisely! You understood what I said, even though I put hats on everything. The alphabet with hats on it is isomorphic to the alphabet I’m using now, because it’s just a meaningless relabeling — a change of abbreviations, if you will. Recognizing that isomorphic things aren’t really different after all makes the Void much less cluttered.
Reader: Oh, I think I get the idea. If two sentences are isomorphic, then they’re saying the same thing, even though it might look like they’re saying something different. Like, if we did arithmetic using Roman numerals, then we could write III + IV = VII, and things like that, but that sentence would really be saying the same thing as 3 + 4 = 7, so the two ways of doing things would be “isomorphic”?
Waitress: Precisely! You’re quick to catch on!
Reader: Really? Does it usually take longer to explain that idea? It seems pretty simple.
Waitress: Well, the explanation we usually use in the Void isn’t exactly the explanation I gave you, but rather an isomorphic explanation of what an isomorphism is. Depends on the dialect, of course, but we usually say something like this: Suppose S and T are two sets, and suppose two binary operations 
and 
are defined on S and T, respectively. Then S and T are isomorphic if and only if there exists an invertible map ϕ from S to T such that for all elements a and b in S we have ϕ (a b) = ϕ(a) 
ϕ(b). See? Exactly the same idea!
Reader: That doesn’t look like the same idea at all!
Waitress: It doesn’t? I can’t tell.
Reader: It made more sense when you just puts hats on the letters. So “isomorphic” things can be the same in every meaningful way, but not the same in terms of how easy they are to understand? Doesn’t that imply that ease of understanding isn’t meaningful?
Waitress: Precisely! And no. Respectively. I’ll put in your order.
Reader: Wait, you still haven’t explained this WKL0 thing. I’d prefer to know what I’m drinking.
Waitress: Don’t worry about what it is. That’s not the point. It’s exactly the same strength as what Author is getting, so they’re the same drink as far as the Void is concerned. In summary, you newcomers should be fine.
(Waitress smiles and leaves the table.)
Reader: I can’t tell whether I’m confused or not.
Stephen Kleene: That’s unfortunate, my friend, but it’s a common feeling at the Beweis Bar. Look on the bright side. Until you have determined whether or not you are confused, at least you can take consolation in knowing with absolute certainty that you are meta-confused.
Reader: I’m not sure that helps.
Stephen Kleene: Precisely!
Reader: . . .
(Waitress returns with the drinks.)
Reader: Wow, that was quick!
Author: Are you sure?
Reader: Oh. . . I guess not. . .
Author: So, Steve! How’s the business?
Stephen Kleene: Business couldn’t be better. How are you three?
Author: Stuck on an invention.
Stephen Kleene: Oh! Might I be of some service? I do love a good invention.
Reader: We’re trying to figure out a way to deal with the area of curvy things.
Stephen Kleene: How are you doing that?
Author: Well, we don’t know how to figure it out, so we also don’t know how we should try to figure it out.
Stephen Kleene: I don’t believe that follows.
Reader: Steve’s right.
Author: Oh. . . Well then how should we try to figure it out?
Stephen Kleene: How have you dealt with these “curvy things” in the past?
Reader: (Pointing at Author) Well, earlier he kept rambling about how the infinite magnifying glass helps with that.
Author: Yeah, but we’ve only used that to find curvy steepness, not curvy area.
Stephen Kleene: And how did you do that?
Reader: Well, we dealt with curvy steepness by zooming in and pretending things were straight.
Author: It felt kind of like cheating, but it worked.
Stephen Kleene: More details, please.
Reader: Well when we were first thinking about curvy steepness, we started by thinking of the curvy thing as the graph of some machine — just for convenience — and then we imagined zooming in. Once we were zoomed in, we just used our steepness definition from Chapter 1.
Stephen Kleene: I believe I have an idea.
Author: Really? What?
Stephen Kleene: See those two sentences Reader just said?
Author: Yeah. What’s your idea?
Stephen Kleene: (1) Replace the word “steepness” with the word “area.” (2) Try that.
Author: Oh. . .
Reader: Oh. . .
Mathematics: OH. . .
The Return of the Magnifying Glass
Author: Alright, so we’ve got some machine M.
Reader: Right.
Mathematics: WHICH MACHINE?
Reader: Best not to decide. Let’s just stay agnostic about which for now.
Author: Okay, so we’ve got some machine that looks curvy when we draw it. Steve suggested we do what we did last time.
Reader: So let’s pick a point on it and zoom in infinitely far.
Mathematics: THEN WHAT?
Reader: Well, now that we’re zoomed in, things look straight. So we might be able to pretend that the tiny amount of area under the curvy thing at that point is just a rectangle.
Mathematics: CAN WE DRAW A PICTURE SO THAT I KNOW WHAT’S GOING ON?
Author: Sure.
(Reader draws Figure 5.3.)
Author: Wait a second. In the picture you drew, there’s some area we’re missing. See that empty triangle? I think we have to fill that in, or else we won’t get the right answer.
Mathematics: THAT MAY NOT BE A PROBLEM!. . .
(Mathematics begins a ((fairly) lengthy)(optional(!))(semi-)digression.)
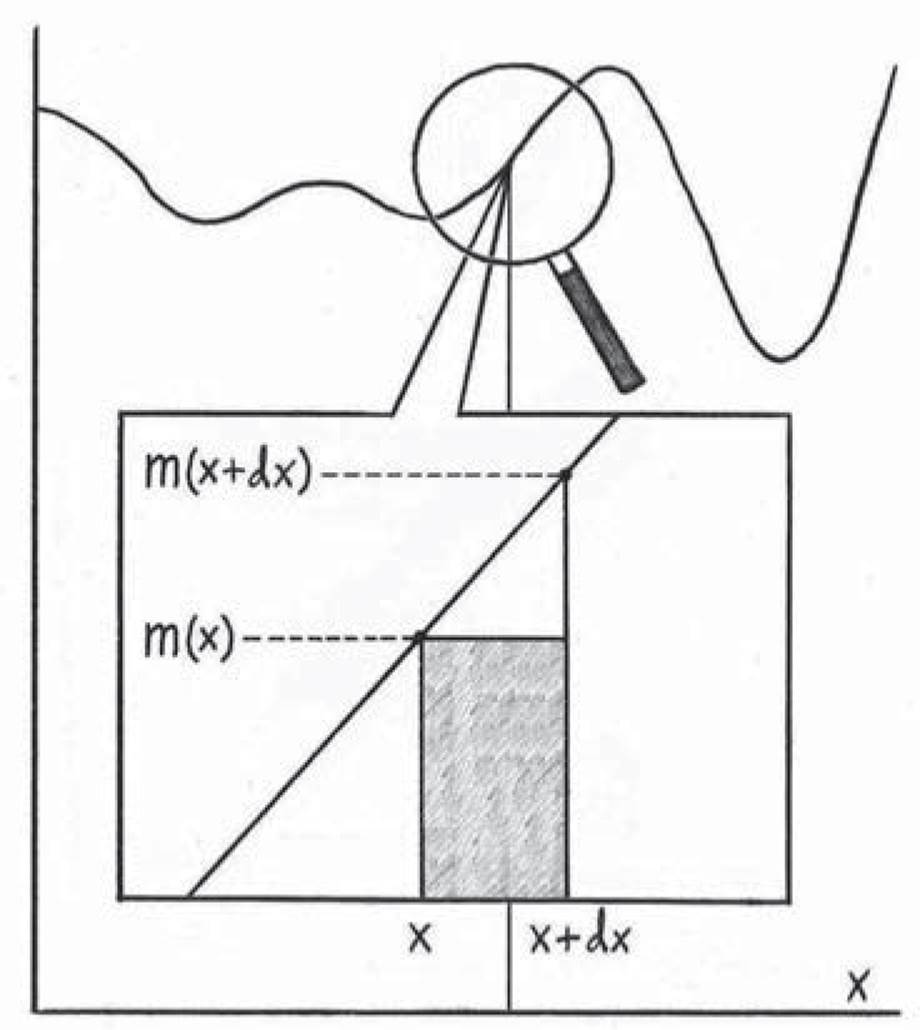
Figure 5.3: Trying to think of a way to use our infinite magnifying glass to calculate the area under curvy things. Our best idea so far is something like this. First step: draw a curvy thing. Second step: pick a place on it and zoom in. Third step: hope that we can write the area under that point of the curvy thing as the area of an infinitely thin rectangle. If we could do that, then the area of each tiny rectangle would just be “length times width,” or m(x)dx. Then we would just have to add up all the tiny areas, one for each point x. So if only we knew how to add up an infinite number of infinitely small things, it seems like we’d be done!
Mathematics: SEE, THESE INFINITELY SMALL NUMBERS SEEM TO COME IN LAYERS, OR AT LEAST THEY ACT LIKE THEY DO. THAT IS, NUMBERS LIKE 3 AND 99 ARE IN SOME SENSE “ONE LEVEL ABOVE” NUMBERS LIKE 7dx OR 52ds, AND TWO LEVELS ABOVE NUMBERS LIKE 6 dx dy OR 99 ds dt. WHEN VARIOUS TERMS WITH MULTIPLE LEVELS ARE ADDED TOGETHER, THERE IS ONE SENSE IN WHICH ONLY THE HIGHEST LEVEL SEEMS TO MATTER. SUCH AS HOW 3 IS INFINITELY CLOSE TO 3 + 2dx, SO WHENEVER WE ASK THE NUMBER 3 + 2dx HOW LARGE IT IS, WE CAN’T TELL ITS ANSWER APART FROM 3. BUT IN ANOTHER SENSE THE LOWER LEVELS MATTER TOO, BEFORE WE ASK THE NUMBER FOR ITS SIZE. THE LOWER LEVELS CAN’T BE IGNORED, BECAUSE AT ANY TIME, SOME OPERATION WE PERFORM MAY CANCEL THE TERMS FROM THE HIGHER LEVELS. WE’VE SEEN THIS IN YOUR DEFINITION OF THE DERIVATIVE. I’LL USE THE TERM“WAFFLING X” AS AN ABBREVIATION FOR “SUBTRACTING THE HIGHEST-LEVEL NUMBER FROM X, AND DIVIDING THE RESULT BY dx.” NOW, IF WE ASK THE NUMBER 9 + 6dx + (dx)2 HOW LARGE IT IS, IT WILL TELL US ITS SIZE IS 9. NATURALLY, THE NUMBER 9 WOULD HAVE TOLD US THE SAME THING ABOUT ITSELF. SO IT MAY APPEAR THAT THE LOWER LEVELS CAN BE IGNORED FROM THE START. BUT THEY CANNOT. THE NUMBER 9 AND THE NUMBER 9 + 6dx + (dx)2 HAVE DIFFERENT BEHAVIORS, AS WE CAN SEE BY WAFFLING EACH. WAFFLING 9 + 6dx + (dx)2 WILL TURN IT INTO 6 + dx, A NUMBER THAT WILL TELL US ITS SIZE IS 6. BUT WAFFLING 9 WILL TURN IT INTO 
, WHICH IS JUST 0. SO WITH INFINITELY SMALL NUMBERS, THE LOWER LEVELS CAN’T BE IGNORED, BUT AS SOON AS WE ASK THE NUMBER TO TELL US HOW LARGE IT IS, THEN ONLY THE LARGEST LEVEL MATTERS.
(Mathematics’s (semi-)digression ends.)
Stephen Kleene: I’m not sure what I think about all that.
Reader: Me neither.
Author: What does this have to do with ignoring the empty triangle?
Mathematics: OH, RIGHT. BACK TO FIGURE 5.3. THE TALL THIN RECTANGLE UNDER EACH POINT x WILL HAVE AREA m(x)dx. THE MISSING TRIANGLE’S AREA WILL BE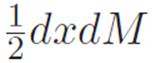 
, WHICH IS ONE LEVEL LOWER. SO WE CAN IGNORE IT, SINCE WE’RE JUST ADDING THE AREAS AND NEVER WAFFLING THEM.
Reader: This is probably scaring me.
Author: Yeah, I have no idea what you just said.
Stephen Kleene: Why do you keep saying “waffle”?
Mathematics: SORRY. . .
Author: I think we can just think about normal rectangles, not infinitely small ones, and then imagine making them smaller and smaller.
Mathematics: HOW SO?
Author: Like this:
(Author draws Figure 5.4, and says everything in its caption.)
Mathematics: WE’RE STILL LISTENING.3
Reader: What? Mathematics: Oh, I suppose that might seem a bit out of order. Go read the caption under Figure 5.4. I’ll wait for you back here.
(Author returns from the caption,
Mathematics returns from the footnote,
Reader seems to have returned from both the caption and the footnote,
Narrator checks his notes to make sure everyone is back. . .
. . .
Oh, and Steve is off with Waitress. . .somewhere.)
Mathematics: (To Author) I THINK I SEE WHAT YOU MEANT IN THE CAPTION ABOUT THAT GIVING ALMOST THE RIGHT ANSWER. I SUPPOSE WE COULD THINK ABOUT IT THAT WAY AS WELL.
Reader: So to make sure I understood the caption, you’re saying the area under the curvy thing will be almost. . . but not exactly. . . this?. . .
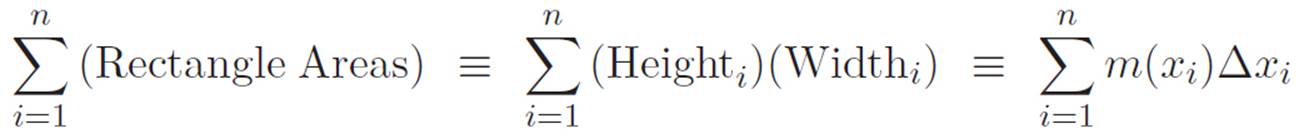
Author: Wow that’s a lot more concise than what I said. But yeah, exactly. That’s what I was getting at.
Reader: And why would we want to do the thing with the rectangles? From the caption?
Author: Oh, we don’t. Or at least I don’t. I mean, the idea about infinitely small rectangles was nicer. But we don’t know how to actually use it yet, to compute anything. So the idea from the caption wasn’t something I think we should actually do. But at least it lets us compute specific numbers. Hypothetically. If we want to. And as we add more rectangles, we’ll slowly be getting closer to the exact answer Mathematics was talking about.
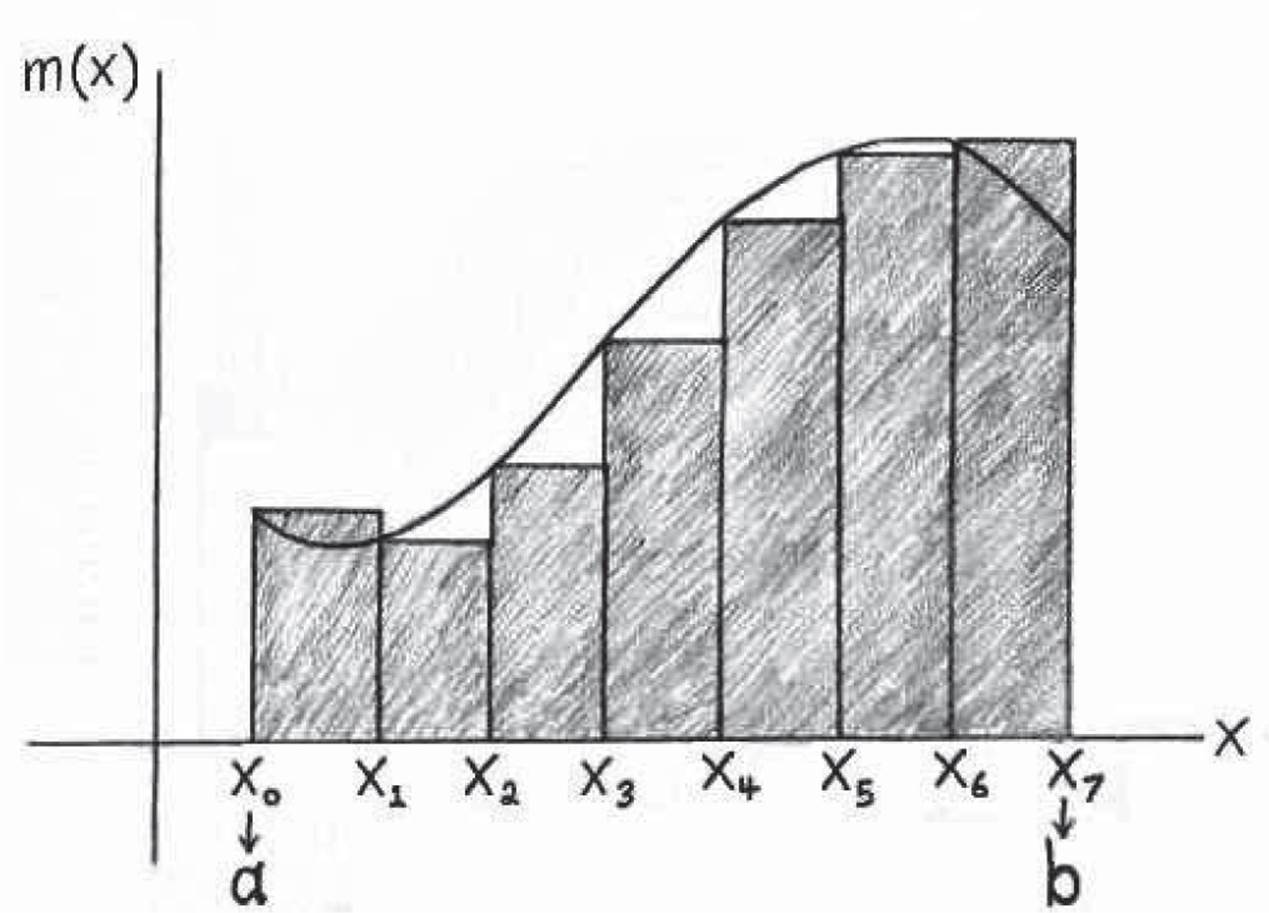
Figure 5.4: Author: Wow, it’s more cramped in here than I expected. So, we’re trying to find the area under a curvy thing between two points x = a and x = b. If thinking about infinitely thin rectangles is too weird, we can just imagine using a finite number of rectangles. Like in the picture. Just imagine picking a bunch of points between x = a and x = b. Let’s give the points names, like x1, x2, . . ., xn, and I guess we could reabbreviate a ≡ x0 and b ≡ xn+1 for convenience. At each of the points xi, the height of the machine’s graph m(xi) will be the height of one of our rectangles. That takes care of height. The width of each rectangle will just be the distance between one point and the next, like in the picture. Each rectangle will have some small width Δxi ≡ xi+1 − xi. So the area of each one will look like “height times width,” or m(xi)Δxi. Then, if we add up all the rectangle areas, we won’t get exactly the right area, but probably something close. And if we imagine adding more and more rectangles and making each one thinner, then we’d be getting closer to the real area. So it’s easy. I mean, easy to imagine. It sounds like a pain to actually do this. So maybe let’s not do it. . . Wow, I’ve been in this caption for awhile. Better go make sure they’re still listening.
Mathematics: I LIKE MY WAY OF THINKING ABOUT IT BETTER.
Author: Me too. I’m ready to give up on this problem.
Mathematics: AS AM I.
Reader: Ooh. Then let’s give up! Can we pull the Molière trick again?
Author: Sure! I mean, that’s what we’ve always done in the past when we decided to give up. Even if we don’t know how to compute the exact answer yet, there’s no harm in naming it. Let’s make sure the name we use for it reminds us of what it is, though.
Reader: Alright, well we wrote the approximate answer like this:
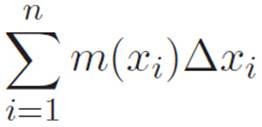
So let’s use this to build an abbreviation for the exact answer. You mentioned awhile back that the textbooks use Δstuff as a shorthand for “a difference in stuff between two points,” because Δ is the Greek capital d, and d stands for difference. Or distance. I don’t think we decided yet.
Author: I don’t think we have either.
Reader: Anyways, because of that, when we invented calculus we needed another way to talk about a difference, but an infinitely small one this time. So we just turned the Greek letter Δ into the Latin letter d. So dx or dt or d(stuff) all just meant a difference in some quantity between two points that were infinitely close together. That made the new idea look kind of like the old one.
Mathematics: HOW DOES THAT HELP US?
Reader: We’re giving up, remember? So we’re pulling the Molière trick and thinking of a good name for the thing we couldn’t figure out.
Mathematics: OH, RIGHT. I FORGOT. SO WHAT SHOULD WE NAME IT?
Reader: Well, I just wrote the approximate answer up there. The one Author described from inside the caption. So let’s take that abbreviation, and replace the Δ with a d, since our rectangles are infinitely thin. That would give us
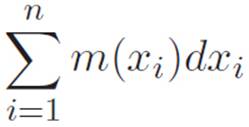
But I guess this doesn’t really mean anything, because we’re changing the abbreviations one at a time.
Author: Nice! Alright, the exact answer should have infinitely many rectangles, one for every point x, so the xi notation doesn’t really work anymore — the i’s just counted rectangles, but we can’t count the rectangles if there’s one at every possible point on a line. So let’s forget about the i’s. And the pieces i = 1 and n don’t work anymore either. Those were just there to remind us where we were starting and ending, but now we can just go back to calling them a and b again. So I guess now our abbreviation is
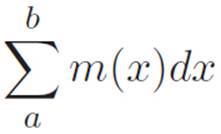
We could just stop here and—
Mathematics: FINALLY! I WAS WAITING FOR YOU TO FINISH. I’M READY TO MAKE MY CHANGE.
Author: Uhh, there’s not much else to change. We could basically just be don—
Mathematics: AUTHOR, THERE ARE THREE OF US. READER GOT TO CHANGE THE GREEK d TO A LATIN d. YOU GOT TO GET RID OF THE SUBSCRIPTS. IT’S ONLY FAIR TO LET ME CHANGE SOMETHING. FAIRNESS IS ABOUT INVARIANCE. DON’T YOU LOVE INVARIANCE?
Author: (Reluctantly) . . . Yes.
Mathematics: PERFECT! I’LL FOLLOW READER’S LEAD. Σ IS THE GREEK LETTER S, AND IT STANDS FOR “SUM.” AS BEFORE, TO TRANSLATE OUR ABBREVIATION FROM THE FINITE TO THE INFINITE, LET’S CHANGE THE GREEK LETTER TO THE CORRESPONDING LATIN LETTER, LIKE THIS:
Reader: What is that?!
Author: Yeah. . . uhh. . . Math? That’s not an S.
Mathematics: LOOK, HOLDING A PEN MAY BE TRIVIAL FOR YOU DIGITLADEN PRIMATES, BUT I’M NOT EXACTLY A PHYSICAL BEING.
Author: We understand. It just looks a bit funny. But let’s keep it that way.
Mathematics: SO WHAT DOES THIS STAND FOR?
Reader: Well, we named it carefully, so we can probably figure it out. The S-like thing reminds us it’s a sum, it’s Latin now instead of Greek, the m(x) is a height, and dx is an infinitely small width. So it stands for a sum of infinitely many things, and each of those things is the area of an infinitely thin rectangle. Oh, and the a and b just remind us where to start and stop.
Author: Great! We successfully pulled the Molière trick!
Reader: So we successfully did. . . nothing?
Author: Well yeah. But we can still write stuff like this:
But you’re right. We still don’t know how to compute this, so we didn’t really “do” anything yet.
Reader: Wait, so after all that we’re still no closer to solving our problem?
Stephen Kleene: Precisely!
(Everyone looks at Steve.)
Author: (To Steve) You weren’t listening to us that whole time, were you?
Stephen Kleene: No, it just seemed like a good time to say “precisely.” I was back at Mathematics’s house. Meta—
Author: Wait, I thought you were with Waitress.
Stephen Kleene: No. You just wrote that I was.
Author: Huh? I don’t remember wri—
Stephen Kleene: Anyways, as I was saying, Meta needed some help, so I went back.
Mathematics: HELP WITH WHAT?
Stephen Kleene: We’ll get to that.
(Steve pulls a small device from his coat and speaks into it.)
Stephen Kleene: Meta?. . . Okay. We’re ready when you are.
Extralude: The Existence Dilemma
(Our characters hear the word “suppose,” followed by something unintelligible, at which point they find themselves back at Mathematics’s house.)
Stephen Kleene: Meta has finished examining the foundation. . . Or foundations, I can never remember which. Plurals are tricky.
Mathematics: AND?
Stephen Kleene: Your house is sinking. . .
Mathematics: MY HOUSE IS SINKING?
Stephen Kleene: Yes. I’m afraid Nature was right. The foundation wasn’t built for a corporeal entity. Well, not corporeal. . . but an entity. You’ve been over this before, right?
Mathematics: I BELIEVE WE HAVE.
Stephen Kleene: You exist now! I was surprised to see the extent of it. Your mismatch with the Void is quite severe, and it will only grow worse with time. The Void is no place for an entity.
Mathematics: OH. . .
Author: Wait, what about you? Don’t you live in the Void too?
Stephen Kleene: Indeed.
Author: Then why don’t you have the same problem?
Stephen Kleene: Modus tollens, friend.
Author: Huh?
Stephen Kleene: You’ve assumed I exist. Check your premises.
Author: What???
Reader: What???
Mathematics: WHAT???
MetaMathematics: . . .
Author: How are you here if you don’t exist?
Stephen Kleene: The Void is home to all things that don’t exist. And one that does. For now. . .
Author: That sounded like foreshadowing.
Stephen Kleene: That sounded like metaforeshadowing.
Author: Like foreshadowing about foreshadowing? I didn’t intend it to be.
Stephen Kleene: No no, metaphor shadowing. Not meta-foreshadowing. Nevermind.
(A curious metasilence elapses.)
Stephen Kleene: (To Author and Reader) Do whatever you can to help Mathematics get out of here and into a new home as soon as possible. One appropriate for this new form it’s taken. It needs to be somewhere it belongs.
Author: Of course. We’ll do anything we can.
Stephen Kleene: Wonderful. On that note, Meta and I must be off. Good luck, you three.
Author: Hope we see you again!
Reader: Bye Steve!
Mathematics: SAY HI TO NATURE FOR ME!
Author: Alright, time for the next chapter. Let’s go!
(Nothing happens. . . Almost as if this spot were already reserved. . .)