Burn Math Class: And Reinvent Mathematics for Yourself (2016)

N. New Is Old

N.1. A Bridge

N.1.1Full Disclosure

(Author and Reader are walking on a locally Euclidean hill in an unknown location.)

Author: This may be my least favorite chapter.

Reader: I don’t think you’re supposed to tell me that.

Author: Come on, really? After all we’ve been through? Why would I hide that from you?

Reader: No, I don’t mind. I just meant we’re taught not to say things like that. . . in places like this.

Author: Why?

Reader: I don’t know. Professionalism?

Author: Yeah. . . I’m not very good at that. . . Even when I need to be. But seriously, why shouldn’t I tell you that this is my least favorite chapter? Wouldn’t hiding that just add to the distance?

Reader: How do you mean?

Author: Like, if I didn’t tell you, and then the chapter didn’t live up to your expectations, you might end up saying, “At first I thought the book was G units of good. . . but then in Chapter N it got a bit [negative adjective]. Then I only thought it was g units of good. . . where g is less than G.”

Reader: You worry a lot. Plus, you were wrong. I didn’t even say those things, with the G and the g and the N. You’re putting words in my mouth.

Author: The alternative is just not to talk to you at all. . .

(An [undefined adjective] silence elapses.)

Reader: So why is this your least favorite chapter?

Author: It’s a bridge.

Reader: A bridge to what?

Author: Somewhere better. Somewhere I really want to show you.

Reader: When will we get there?

Author: Soon. In the final chapter. I’m thinking of calling it Chapter .

Reader: What does the stand for?

Author: Nothing. It’s the Hebrew letter aleph. It’s used to represent the infinite.

Reader: I thought ∞ was used for that.

Author: It is. Different thing. The symbol ∞ stands for the non-numerical limit past the end of the real numbers. It’s used in different ways. Usually just to mean that a sequence grows without bound. But it’s a symbol that describes behavior, not really a symbol that describes a number or an honest mathematical object. There are exceptions, of course. Some people use it differently. People get squeamish about the infinite.

Reader: So what’s ?

Author: A better kind of infinity.

Reader: Better?

Author: Well, no. It’s an aesthetic preference. But it’s a symbol built by people who weren’t squeamish. Who took the idea seriously. It’s used in the formal theory of the infinite. To stand for different sizes of infinity. They’re called “transfinite cardinals.” We won’t have time to talk about them. . . god, there’s so little time left. . . Honestly, calling it Chapter ∞ might have been more accurate. But Chapter seemed right. More genuine, somehow.

Reader: I don’t mean this in a mean way, but. . . do I need to know all this?

Author: No. But Chapter is where I want to get us to. It’s about calculus in an infinite number of dimensions. It’s beautiful. None of the books convey how simple it is. So I want to show you.

Reader: So why not start there?

Author: We need this chapter first. As a bridge. It’s not so bad, I guess. The topic itself is wonderful. I just don’t feel like I did it justice.

Reader: Did what justice?

Author: The subject of this chapter.

Reader: What’s that?

Author: Multivariable calculus.

N.1.2What’s a Multivariable?

Reader: What’s a multivariable?

Author: Hah, nothing. The word is used like an adjective, not a noun. I just thought it would be a fun section title.

Reader: So what does it mean? I mean, I’ve heard the word “variable” before.

Author: Where?

Reader: In this book.

Author: I’ve never said that word before.

(Reader flips back through the book.)

Reader: Yes you have!

Author: I have?

(Author flips back through the book.)

Author: Hmm. . . I suppose I have. My memory hasn’t been the best lately. Remind me what a “variable” is again.

Reader: The textbooks’ name for the food we feed our machines.

Author: Oh, okay. That’s a weird name.

Reader: And they also use the word to refer to what the machines spit out.

Author: What? Why?

Reader: I think it’s because we can choose to feed the machines different things. . . so what we feed it can vary. . . so it’s “variable.”

Author: Oh right, I remember. And our machines can also spit out different things depending on what we feed them, so by that logic, what they spit out is a “variable” too.

Reader: Yeah.

Author: Okay. Then what’s a multivariable?

Reader: You just said yourself it’s not a noun. But still, “multi” means “more than one,” so maybe “multivariable” just means “more than one variable.”

Author: Hold on, I have a question. You just said they use the word “variable” for the stuff we feed the machines and the stuff they spit out.

Reader: So?

Author: So we’ve already got more than one variable! How are we not already doing multivariable calculus?

Reader: Well I guess we are. In an unimportant sense. But that’s just nitpicking about terminology. Before we can understand the terms I think we have to invent it.

Author: Invent what?

Reader: Multivariable calculus.

Author: How do we do that?

Reader: I don’t know. Even if we are already doing “multivariable calculus,” in the nitpicky way you just mentioned, the word “multi” doesn’t just mean two. . . so why stop at two?

Author: How do you mean?

Reader: What if we build a machine that eats two things and spits out one thing?

Author: Oh. . . Or maybe eats one thing and spits out two things?

Reader: Exactly!

Author: Or eats two things and spits out two things?

Reader: Or eats n things and spits out m things?

Author: Hah! Or eats infinitely many things and—

Reader: Let’s not get carried away. You said yourself this was a bridge.

Author: Who cares? Let’s try it! All of it!

Reader: But we don’t know how to try it.

Author: So?

Reader: I mean, I know how to make abbreviations and stuff, but. . .

Author: How?

Reader: Well, for a machine that eats two things and spits out one thing, we could call the machine m as usual, we could call the two things we feed it x and y, and we could call the one thing it spits out m(x, y). And if a machine eats n things and spits out one thing, we could write m(x, y, z). . . Oops, I ran out of letters. I mean, we could write m(x₁, x₂, . . . , x_n).

Author: What about the other stuff?

Reader: Like a machine that eats one thing and spits out two things?

Author: Sure.

Reader: Well, we could write m for the machine, x for the thing it eats, and then use a and b for the two things the machine spits out.

Author: Sounds good. But wait, our old abbreviation for “the thing a machine spits out” reminded us that the output might depend on what we put in. I’ll forget that unless we remind ourselves.

Reader: Oh, okay. Well we could write m for the machine, x for the thing it eats, and then use f(x) and g(x) for the two things the machine spits out.

Author: Nice! I just had an idea. Remember before how you wrote m(x, y) for a machine that eats two things and spits out one thing? What if we think of this as a machine that eats one big thing and spits out one thing? The thing it eats is still a thing, but it’s not a number anymore, it’s a list of two numbers: that weird (x, y) thing you wrote.

Reader: Either way. I wasn’t thinking of (x, y) as a single thing when I wrote it, but I guess the word “list” makes it sound like one thing. Sure. Think about it that way if you prefer. Ooh! And then we could do the same thing for the “one in, two out” machine and write it as m(x) ≡ (f(x), g(x)).

Author: And then we could do calculus on these things!

Reader: But we don’t know how to do calculus on them. I can abbreviate stuff no problem, but. . .

Author: Who cares! Let’s try it!

N.1.3What Do We Do When We Don’t Know What to Do?

Reader: What do we do to something new if we don’t know what to do to things that are new?

Author: I’m pretty sure I don’t know the answer to that.

Reader: Why not?

Author: By definition.

Reader: Then what do we do?

Author: The only thing we can.

Reader: What’s that?

Author: Let’s not do anything new.

(Crickets.)

Reader: That doesn’t seem like a very intelligent idea.

Author: It’s not! Let’s try it!

Reader: How?

Author: Well, how did we invent the “derivative” originally?

Reader: We used our slope idea from Chapter 1 on two infinitely close points.

Author: How’d we do that?

Reader: Well, we had a machine m, we fed it some food x, and it spat out m(x). Then we made a tiny change dx to the food, changing it from x to x + dx. We fed the machine the new food, and it spat out m(x + dx). Then we looked at the difference in the machine’s behavior before and after, which is to say

d(Output) ≡ Output_after − Output_before

or to write the same thing in a different way,

dm ≡ m(x + dx) − m(x)

Author: Exactly, and the derivative was just

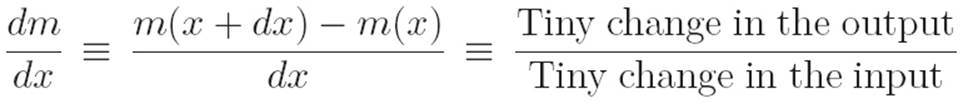
So let’s try to do that for our new machines!

Reader: Seriously?

Author: Why not? Let’s try some of the machines we just made abbreviations for.

Reader: Which one should we try first?

Author: I don’t know. Pick your favorite.

Reader: Let’s try m(x) ≡ (f(x), g(x)). But what if what we do doesn’t make sense?

Author: Don’t worry! We’ll try to make sense of what we did later. If it doesn’t make sense, we’ll just keep punching it until it does.

Reader: Uh. . . okay. Here we go. Let’s define m(x) ≡ (f(x), g(x)). Then if we use the same definitions as we did in the single-variable case, we can write

dm ≡ m(x + dx) − m(x) ≡ (f(x + dx), g(x + dx)) − (f(x), g(x))

Reader: I’m stuck. We don’t know how to add or subtract two lists. What do we do?

Author: Just do the simplest thing you can think of.

Reader: What’s the simplest thing I can think of?

Author: I don’t know. You think of it.

Reader: Well, we don’t know how to add lists, but we do know how to add numbers, so maybe whenever we see two lists added, we could just add slot by slot, like this:

(a, b) + (A, B) ≡ (a + A, b + B)

Same deal with subtraction. I guess if we do that, then the new idea of addition is just the old idea. How do we know if this worked?

Author: You say, “It worked!”

Reader: It. . . worked.

Author: Nah, say it more maniacally, like you just captured Batman in your shark tank.

Reader: It worked!!!

Author: That’s more like it!

Reader: There’s no way that’s enough.

Author: Sure it is! List addition isn’t something “out there in the world” that we might accidentally say something wrong about. We can just define it to behave in whatever way makes life easiest for us. Like when we invented powers back in Interlude 2.

Reader: Okay. Then I guess we can pick up where we left off. Now that we’ve said what adding and subtracting lists means, we can write:

dm = (f(x + dx) − f(x), g(x + dx) − g(x))

so the “derivative” would be

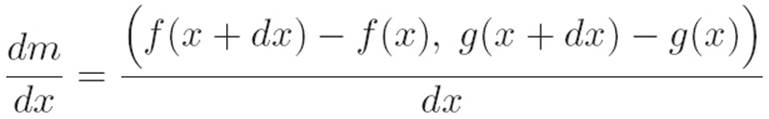
Reader: I’m stuck again.

Author: Why?

Reader: Well, I know that dx is just a tiny number, and division by stuff is just multiplication by 1/stuff, so I guess I could write

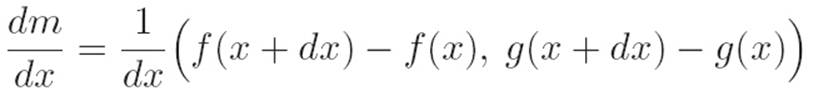
but that doesn’t get us any less stuck. We still don’t know how to multiply a number by a list.

Author: How about we just do the same thing as before?

Reader: Okay. I don’t know how to multiply a number by a list, but I do know how to multiply a number by a number, so I guess we can just define “number times list” to be multiplying slot by slot, like this:

c · (x, y) ≡ (cx, cy)

If we do that, then we’re unstuck again, and we can write

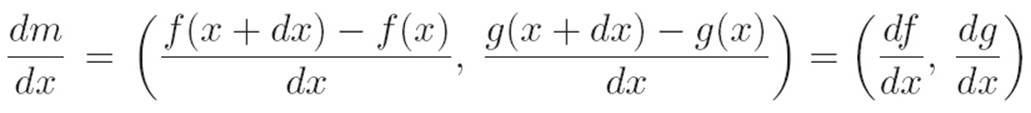
So I guess the derivative of these weird new machines is just the old derivative in each slot.

Author: That wasn’t as hard as I expected. Let’s write it in a box to celebrate!

What We Just Invented

If m is a machine that eats one thing and spits out two things, so that

m(x) ≡ (f(x), g(x))

and if we define the sum of two lists in the dumbest way we can think of, like this:

(a, b) + (A, B) ≡ (a + A, b + B)

and if we define “number times list” in the dumbest way we can think of, like this:

c · (x, y) ≡ (cx, cy)

then the derivative of our new kind of machine is

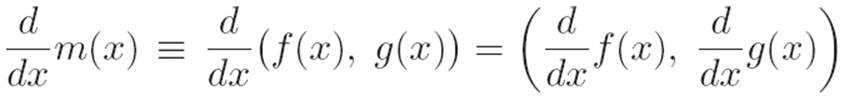
or to write the same thing in another way,

m′(x) ≡ (f(x), g(x))′ = (f′(x), g′(x))

So in this case, the new “multivariable calculus” idea is nothing new. It’s just our old familiar calculus ideas in each slot.

Reader: You know, you keep saying that this new stuff is nothing new, but I still don’t feel very comfortable with it. It just feels too. . . new.

Author: It’s not new.

Reader: Yeah, I know, but can we do a few examples?

Author: Sure. How’s about we try to figure out the derivative of the machine m(x) ≡ (2x, x³)?

Reader: Okay. Well, because of everything we just did, I guess the derivative is m′(x) = (2, 3x²).

Reader: Is that right?

Author: Who am I to say? You’re acting like someone already invented this stuff. Like facts about it are sitting around in some dusty book somewhere. What we just did has to be true because of how we defined (i) list-plus-list and (ii) list-times-number. You tell me if it’s right.

Reader: Okay, I guess it is.

Author: Great! Let’s do another example. Say we define a new machine m to be:

m(x) ≡ (x² + 7x, e^2x + H(x))

How would we differentiate that?

Reader: Well based on everything we just did, the derivative of a list is just the list of the derivatives, so I guess the derivative is

m′(x) = (2x + 7, 2e^2x − V (x))

where I used the hammer for reabbreviation to differentiate e²x. Also, I had to look back to what we did earlier to remember that we showed H′ = −V back in Chapter 4.

Author: Alright! Let’s go on to the next secti—

Reader: Wait. Calculus wasn’t just derivatives, right? I mean, “calculus” was the name we came up with for all the weird things we could do with our infinite magnifying glass. At first it was just derivatives, but later we came up with that “integral” idea, remember?

Author: Oh, right. But that was just addition, wasn’t it?

Reader: Kind of. I mean, the symbol was our abbreviation for the area under a curvy thing m between x = a and x = b. And the abbreviation came from thinking of adding up a bunch of infinitely thin rectangles. So the ∫ thing had a kind of addition-ish interpretation, but it didn’t exactly feel like addition.

Author: So? Feelings are goofy. I feel all sorts of incorrect things. It was still just addition.

Reader: So how do we integrate these new machines?

Author: I don’t know. Let’s see.

Reader: Well, say we want to make sense of something like 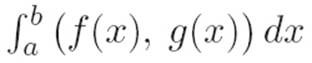. That dx thing is just an infinitely small number, so I guess because of how we defined number-times-list, we can write this as .

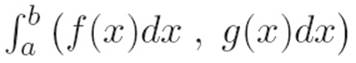Author: And we defined list addition to let us bring the + inside, so I guess it makes sense to bring the ∫ inside, since that was just addition too. Like this:

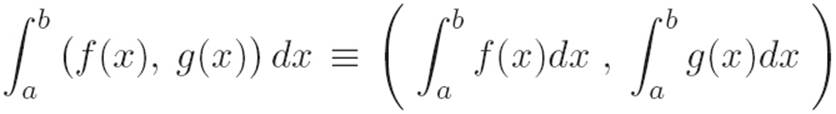
Reader: So the integral of a list is just a list of both the integrals?

Author: I guess so!

Reader: But how do we know this is right?

Author: Same deal as last time. We’re not really doing mathematics. Or, we are, but not quite. If it makes you more comfortable, just think of that argument as “pre-mathematics.” The logic is backwards when we’re inventing things. When we’re inventing a new idea, we just use old ideas until we get stuck. Then we introduce some new assumption that lets us get unstuck. The trick is to get unstuck using as few assumptions as possible. That way, the mathematics we end up inventing will be “elegant.” But it’s not the kind of argument that we might be right or wrong about.

Reader: Still, I don’t feel super-familiar with this yet. Can we do some examples?

Author: Sure! Let’s undo the example from earlier. Say we’ve got the machine m(x) ≡ (2, 3x²). What’s the integral of m(x) from x = 0 to x = 7?

Reader: Well, using what we just invented, and writing where we use the fundamental hammer, I guess we could write:

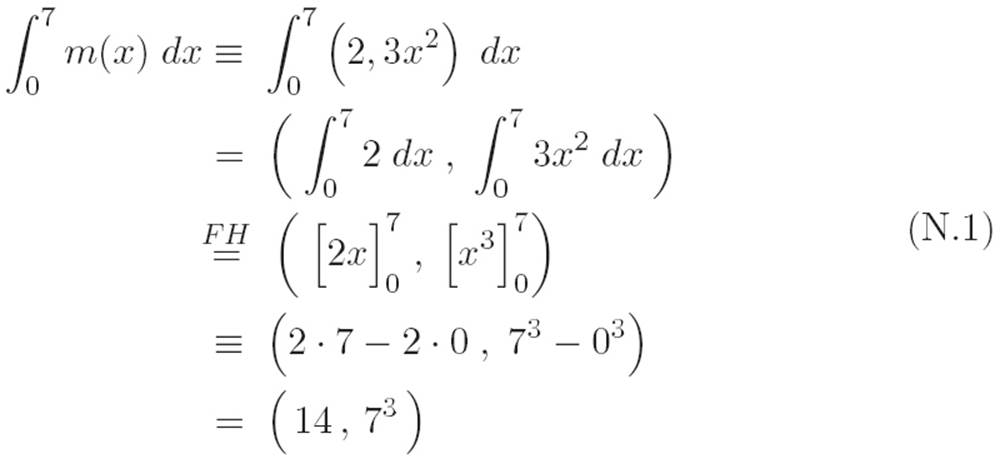
Reader: Remind me what 7³ is, would you?

Author: A number.

Reader: Which number?

Author: Who cares? Just leave it as 7³. Arithmetic makes me tired. Back to the ideas. What ideas did you use in the derivation you just did?

Reader: Let me see. I think I just used the fundamental hammer and the fact that “the integral of a list is the list of the integrals.” The other steps were just abbreviations and arithmetic. Is that really all there is to it?

Author: It has to be! These new ideas aren’t new!

Reader: Yeah yeah, but that was a pretty easy example. What if we couldn’t manage to think of an anti-derivative of one of the slots?

Author: Well, what did we do when we couldn’t think of an anti-derivative back in regular calculus?

Reader: (Flipping back to Chapter 6) We could use one of the three anti-hammers to rewrite the problem. Can we do that if we get stuck in multivariable calculus?

Author: Of course.

Reader: How do we know they still work in. . . oh, right. It’s just regular calculus in each slot. They have to work. Well what if we tried that, and we were still stuck? Then what?

Author: Exactly what we did before: give up! We never got to a point in regular calculus where we could solve any imaginable problem. We’re not omniscient now, and we never were. By definition, we can only solve problems that we can solve. If we can’t solve a problem using the tools we’ve invented, then we can’t really do much except keep banging our heads against it, or just sweep it under the rug and come back to it later if we want to.

N.1.4Wait. . . Seriously?

Reader: Wait. . . seriously? So the new stuff is really nothing new?

Author: Well, it depends on what the meaning of the word “is” is. We forced the new to be nothing new, because life is easiest if we do things that way. Truly new stuff is definitely something new, by definition, but we defined our new stuff not to be anything new, at least this time.

Reader: I’m confused.

Author: Don’t be. There’s nothing to be confused about.

Reader: Okay. . . now what?

Author: I don’t know. That’s up to us. I’m having fun with this “multivariable calculus” idea, so let’s play around with that some more.

Reader: Alright, what haven’t we done?

Author: (Looks back) We haven’t looked at machines that eat two things and spit out one thing.

Reader: Right. Let’s say we’ve got a machine that eats two things x and y, and spits out one thing m(x, y). Then, uh. . . what do we do?

Author: I don’t know. What did we do at this point in single-variable calculus?

Reader: We made a tiny change in the food that we fed to the machine, changing it from food to food + d(food).

Author: Hmm. . . We’ve got two slots. What counts as the food? Ooh! I’ve got an idea. . .

(Author begins writing something.)

Reader: I guess we could just do each slot individually. Then we’d have two different derivatives.

Author: Huh? Sorry, I wasn’t listening. I was thinking that we could think of the whole list as the food, and write something like v ≡ (x, y). Then a tiny change in the food might be something like a “tiny list,” whatever that means, which we could abbreviate as dv ≡ (dx, dy). What were you saying?

Reader: I was saying that we could just choose to do each slot individually, which would give us two different ways to “do derivatives,” one for each slot.

Author: Oh! I like that idea better. Forget what I said — let’s do yours first. What do you mean by two different derivatives?

Reader: Well so far we’ve been dealing with new stuff by not doing anything new, and just doing the old stuff. So how about this: we’ve got this machine m that eats two things x and y and spits out one thing m(x, y). First, I guess we could think of the food as x, leaving y alone. We make a tiny change in the food, changing it from x to x + dx. Then, as always, we compare the machine’s output before and after, which means we’re looking at d(Output) ≡ Output_after − Output_before, or equivalently

dm ≡ m(x + dx, y) − m(x, y)

Author: Wait, you said you’re going to do this for y too, right?

Reader: Yeah, why?

Author: I’m a bit confused. What abbreviation do we use when we’re changing y instead of x?

Reader: I suppose we’d just write dm ≡ m(x, y + dy) − m(x, y). . . Oh, I see the problem. I wrote dm as an abbreviation for both. But based on how I defined them, they’re really two different things. How about I just change abbreviations, and write something like this?

d_xm ≡ m(x + dx, y) − m(x, y)

d_ym ≡ m(x, y + dy) − m(x, y)

Author: Oh, okay. That makes a bit more sense.

Reader: Then I guess we could define the derivative of m with respect to x to be the thing you get from dividing d_xm by dx, like this

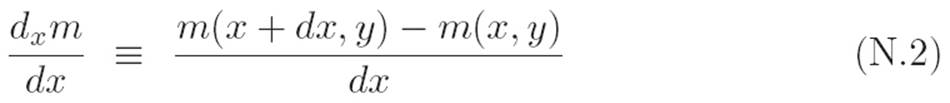
and we could define the derivative of m with respect to y to be

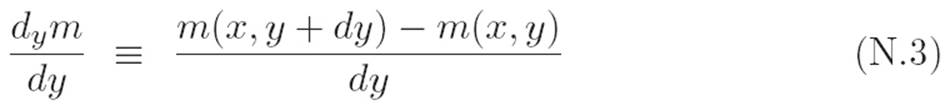
Author: What about the other two possibilities, d_ym/dx and d_xm/dy?

Reader: Uh, I dunno. I don’t see how those mean anything.

Author: Really?

(Author looks back at how everything was defined, and thinks for a moment.)

Author: Oh! I see. You’re right. We can change x without changing y, just like we can go east without going north. If we want the derivatives to have the normal interpretation as some kind of steepness, then those two things I just wrote don’t really make sense. It’s like dividing the “rise” of Mount Everest by the “run” of the Appalachian Trail. I guess we’re free to write stuff like d_xm/dy if we want, but it isn’t really talking about anything worth talking about, so let’s just ignore it.

Reader: Deal! Now what?

Author: I don’t know. I think we’re done.

Reader: Are we?

Author: I think so. The definitions you wrote down in equations N.2 and N.3 tell us how to figure out both kinds of derivatives. And hey! This “new” idea is still nothing new! I mean, the derivative of the “two-variable machine” m(x, y) with respect to x is just the thing we get from pretending that y is a constant, like 7 or 52, and then doing regular old calculus on it! Same deal for the derivative with respect to y.

Reader: Wait, how do you know that?

Author: That’s what you said in equations N.2 and N.3. I was just looking at what you wrote.

Reader: Nice! Does that mean we can use our old derivative hammers on these machines too? I mean, I know we could use them on the “one in, two out” machines from earlier. But there are two different types of derivatives now. Can we really keep using our hammers in exactly the same way? How do we know they’ll work?

Author: They have to! The new ideas are just the old ones!

Reader: Okay, I understand how the new stuff isn’t new, but it still feels new.

Author: It’s not just you. A slight change of abbreviations can be pretty confusing to all of us. Or it can help. The human mind is funny that way. Let’s do a few new examples to get ourselves used to this old idea. I’ll define m(x, y) ≡ x²y + 7y² − 12xy + 9. Now what’s the x-derivative of that?

Reader: I guess

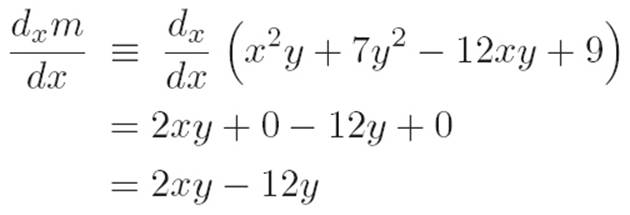
Is that right?

Author: What do you mean?

Reader: What do you mean what do I mean?

Author: Let’s say we were back doing regular calculus, and you were trying to differentiate x²# + 7#² − 12x# + 9. Would you be as cautious about whether you got the “right” answer then?

Reader: I guess not. I’m more familiar with regular calculus. Or single-variable, I mean.

Author: Well that’s all we’re doing here, remember? We’re free to wonder whether or not we “did the right thing,” but only if we’re unsure about whether we did the single-variable calculus right, because that’s all this is.

Reader: I mean, I know that. You’ve said it an annoying number of times by now — but it still feels like this new stuff is new.

Author: Then let’s do another example. I’ve been wondering something since we defined these partial derivatives. Remember at the end of Chapter 2, when we talked about how the derivative lets us find the places where a machine is highest and lowest?

Reader: Maybe I remember. Maybe not. No way to tell.

Author: Well flip back if you don’t remember. The basic idea was that the highest point of a machine’s graph should also be a place where the slope is zero. Same goes for the lowest point. There were some exceptions, but let’s worry about that later. Even if we couldn’t picture the graph of a given machine, we could still usually find its highest and lowest points. Or at least trim down an infinite number of possibilities to some small finite number that we’d have to check by hand.

Reader: Can we do that here?

Author: That’s what I’ve been wondering. Maybe we can find maximum and minimum points by forcing both partial derivatives to be zero.

Reader: Let’s see. How do we start?

Author: Let’s try something simple enough that we know where it has its minimum. Like m(x, y) ≡ x² + y². When x and y are both 0, then m spits out 0, but squaring stuff always makes it positive, so I guess the smallest thing it can ever spit out is m(0, 0) = 0.

Reader: Oh, I think I get it. Based on the way we defined partial derivatives, we can write

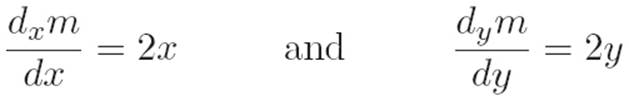
And if we force both of these to be equal to zero,

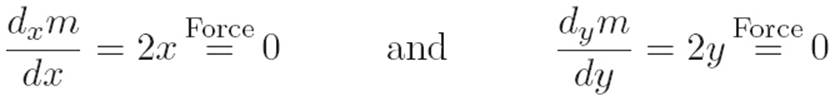
then that’s equivalent to saying x = 0 and y = 0. Hey, it worked!

Author: Nice! Will this work in more complicated cases?

Reader: I don’t know. Let’s look at m(x, y) ≡ (x − 3)² + (y + 2)². Now, for the same reasons as before, this will spit out zero when x = 3 and y = − 2. Anywhere else it’s bigger. And hey, just to see what happens, let’s unwrap the machine and see if the mathematics tells us that that’s where the minimum happens.

That’s the same machine, because I just multiplied everything out, but when we write it this way it’s not obvious that the minimum is at x = 3 and y = − 2.

Author: Wait, why are you expanding everything out if it just makes the minimum less obvious?

Reader: Because all this stuff is only useful if it does something we can’t do without it. I mean, a way of finding biggest and smallest locations is only useful when it’s not obvious how to find them by just staring at the description of the machine. But if this “set both partial derivatives equal to zero” technique is really on the right track, then it ought to spit out x = 3 and y = − 2 when we apply it on this more confusing description of the machine I just wrote in equation N.4.

Author: Brilliant! Let’s try it!

Reader: Okay, taking the two partial derivatives of equation N.4 and forcing them to be zero, we get

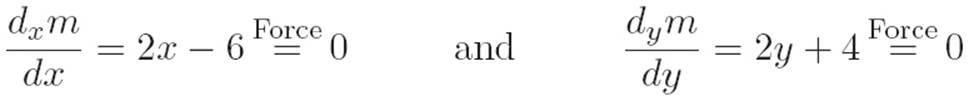
Hey! The first equation is only true when x = 3, and the second one is only true when y = − 2. It worked!

Author: This is great! You feeling more comfortable with this stuff now?

Reader: A bit, but it still feels new.

Author: It’s not.

Reader: I know. Can we do one more example?

Author: Of course. What kind?

Reader: How about an integral this time? Say

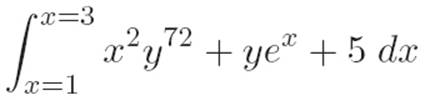
If we’re thinking of y as a fixed number like 7, then I guess it behaves just like 7 would. So an anti-derivative of the thing inside the integral would be . And now I guess we can use the fundamental hammer.

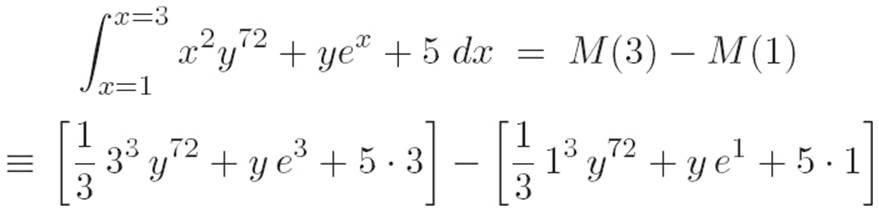
Author: Great! We’re done!

Reader: No no no. I know simplification is a human construct and all that, but I want to clean it up just a little. I mean seriously, there’s a 1³ in there. The stuff above is just. . .

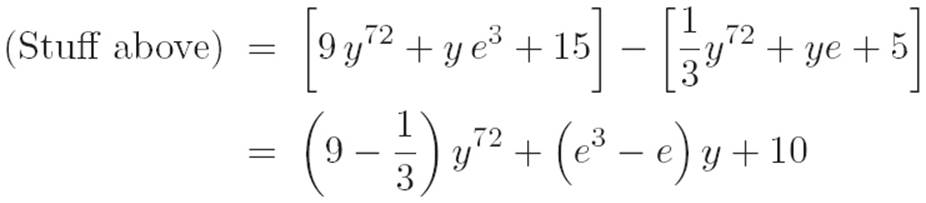
Now I could find a common denominat—

Author: What?! What have they been teaching you in school? We’re so done.

Reader: Okay. It’s just that after so many years in school, it’s easy to develop this compulsive feeling that things need to be “simplified.”

Author: Compulsions are fine, as long as they’re your own compulsions. I’ve got plenty! But don’t waste your time trying to satisfy someone else’s compulsions. Otherwise, simplification just complicates things.

Reader: Alright, so I guess we’re done. Wait, are we really done? The integral still has a y in it.

Author: Yeah, that’s weird.

Reader: Hang on — I think that’s okay. We just calculated the area under the machine m(x) ≡ x²y⁷² + ye^x + 5 between x = 1 and x = 3. But we’re choosing to remain agnostic about which particular number y is, so I think we just did infinitely many integrals at once. I mean, each different choice ofy gives us a different “single-variable machine.” Like, when y is 1, what we just figured out tells us

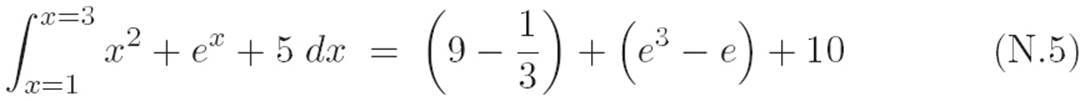
And when y = 0, what we just figured out can be summarized by writing

We never specified what y was, so it’s not a bad thing that it showed up unspecified in the answer. So by staying agnostic about y, we get to say impressive things like “We just did an infinite number of integrals.” Because the answer we got was really infinitely many sentences: one for each y. Some of the sentences were sort of scary-looking, like equation N.5, and some of the sentences seemed simpler, like equation N.6, which just says that a rectangle with height 5 and width 3 − 1 = 2 has an area of 10. So the sentence with y = 0 feels simpler to us than the sentence with y = 1, but the mathematics doesn’t care. The same calculation spits out both. Hey, that reminds me. Where is Mathematics?

Author: Still looking for a new home, I guess. I felt bad about having delayed the moving process in the last interlude.

Reader: You did what?

Author: Remember? I was all caught up in the idea of slaying . But we’re supposed to be helping Mathematics find a home—somewhere it belongs, now that it exists. So much of it exists now. Living somewhere that doesn’t. . . or, at least not in the everyday sense. . . it’s not going well. The Void is no place for an entity. So I’m giving it a break from these dialogues. It needs some time to work this whole situation out.

Reader: Wait, so aren’t we doing the worst possible thing right now?

Author: What do you mean?

Reader: We’re inventing more mathematics! Isn’t that making the situation worse?

Author: No no, we’re not inventing anything new, remember? I made sure of it. Look at the title of the chapter. We wouldn’t want to do that to our friend.