Burn Math Class: And Reinvent Mathematics for Yourself (2016)

This section contains translations of the nonstandard terms used in this book into more standard terminology, and vice versa. This is not a complete list of all the mathematical terms used in the book, but only of the ones I made up.

From Our Terminology to Standard Terminology

Cannibal Calculus

Our name for what textbooks call the “calculus of variations,” used in Chapter . This refers to using the tools of calculus on what textbooks call “functionals” (see Cannibalistic Machines in this dictionary).

Cannibalistic Machines

Our name for what textbooks call “functionals,” used in Chapter . This refers to “big machines” that eat an entire machine and spit out a number, as opposed to simpler machines like f(x) ≡ x², which simply eat a number and spit out a number. For example, the following are three examples of cannibalistic machines:

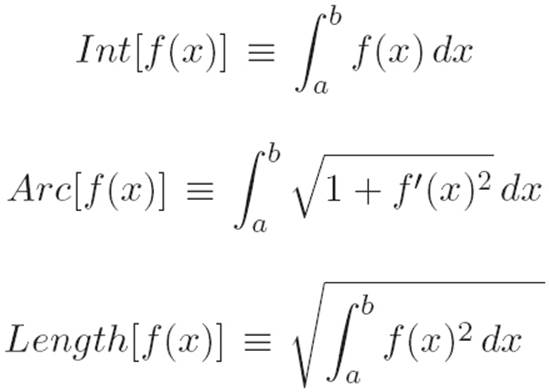
The first example is a cannibalistic machine that eats a machine f(x) and spits out the area under its graph between two points x = a and x = b. The second example is a cannibalistic machine that eats a machine f(x) and spits out the length of its graph between two points x = a and x = b. The third example is a cannibalistic machine that eats a machine f(x) and spits out the “length” of the machine when interpreted as a vector with infinitely many slots (i.e., as a point in a space with infinitely many dimensions). The interpretation of this third example as a “length” comes not from the length off’s graph, but simply from writing down a generalization of the formula for shortcut distances that applies to infinitely many dimensions (see Chapter for a more detailed discussion).

Formula for Shortcut Distances

Our name for what textbooks call the “Pythagorean theorem” (for a simple visual explanation of why this is true, see the beginning of Interlude 1). This formula is also the reason for several of what textbooks call “trig identities.” For example, since sine and cosine simply refer to the vertical and horizontal lengths of a tilted line of length 1 (see V and H in this dictionary) the formula for shortcut distances tells us that

(Vertical length)² + (Horizontal length)² = (Total length)²

which in this case reduces to

sin(x)² + cos(x)² = 1

Textbooks often throw around other “trig identities” that arise from the above equation by giving unnecessary names to things. For example, if we divide both sides of the above equation by cos(x)², we get

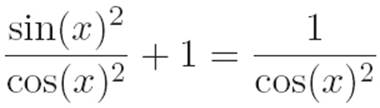
Then, following the textbook-y convention of using tan(x) to stand for 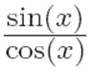, and sec(x) to stand for 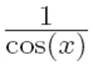, this becomes

tan(x)² + 1 = sec(x)²

Therefore, this so-called “trig identity” is simply the formula for shortcut distances, hiding behind a series of arcane names for simple combinations of V and H.

H

Our name for what textbooks call “cosine.” We use this name to stand for the word “horizontal.” Used because a straight line tilted at an angle α relative to the horizontal axis will have a horizontal length of cos(α), which we instead call H (α). Also see V for what textbooks call “sine.”

Handstand

Our name for what textbooks call “reciprocals.” For example, the handstand of 3 is . We don’t use this term very often. But then again, mathematicians don’t use the word “reciprocal” that often. Maybe we don’t need either one.

Infinite Magnifying Glass

This term has no direct analogue in the standard textbooks, though it is related to the concepts of local linearity and of limits. The infinite magnifying glass is an imaginary tool that lets us zoom in on anything with an infinite amount of magnification. It was used to motivate the central ideas of calculus: by zooming in infinitely closely on curvy stuff, it appears straight. By imagining this process of infinite magnification, we can essentially reduce problems involving curvy things to simpler problems involving tiny straight things, which can be solved by easier methods. See Chapter 2 for a detailed discussion.

Machines

Our name for what textbooks call “functions.” Used throughout the book.

Obvious Law of Tearing Things

Our (admittedly playful, and infrequently used) name for what textbooks call the “distributive property.” This is a property relating addition and multiplication, which says that for any numbers a, b, and c, the following is true:

a(b + c) = ab + ac

(b + c)a = ba + ca

Because the order of multiplication doesn’t matter for numbers, we have ab = ba and ac = ca, so the two lines above are equal to each other when a and b are numbers (though they may not be equal when a and b refer to more general objects, as we’ll discuss briefly below). We used the term obvious law of tearing things because, if we think of a(b + c) as the area of a rectangle with length a and width b + c, the distributive property can be interpreted as saying that area doesn’t change when you tear the rectangle into two pieces. The term is used mostly in Chapter 1.

Although we didn’t discuss abstract algebra at length in this book, we can define “distributive properties” in a much broader context. In general, a distributive property is a statement saying that two binary operations are related somehow. What’s a binary operation? Well, given two objects¹ aand b, a binary operation is an abstract way of banging these two objects together to get a third object a b. In abstract algebra, a binary operation is said to “distribute” over another binary operation if the following two sentences are true for all objects a, b, and c:

These “objects” may be numbers, or they may be something else, like matrices (not discussed at length in this book) or functions.

Notice the similarity with the more familiar version for numbers up above. Historically, the simple version for numbers was recognized first, and then later generalized to wilder and weirder settings.

Nostalgia Device

Our name for what textbooks call “Taylor series” and “Maclaurin series.”

Plus-Times Machines

Our name for what textbooks call “polynomials.” We use this name because these are the machines that can be described using only addition and multiplication. A plus-times machine is defined to be any machine of the form

m(x) ≡ #₀ + #₁x + #₂x² + · · · + #_nxⁿ

where the symbols #i stand for any fixed numbers.

Sharp

Written , this is our name for what textbooks call π. See the first section of Chapter 4 for its definition, and for a discussion of why we’ve chosen not to use the standard notation. In short: we are calling it to remind ourselves that it is a number that we define by its behavior, and which we can make use of conceptually long before we know its specific numerical value (which we finally compute for ourselves in Interlude 6, “Slaying Sharp”). Since the symbol π is so familiar to most readers, calling this concept π makes it easy to forget that — for the majority of our journey — we do not in fact “know” that this number is approximately equal to 3.14.

Shortcut Distance

Our name for what textbooks call a “hypotenuse.” Also see Formula for Shortcut Distances.

T

Our name for what textbooks call “tangent,” used briefly in Interlude 6, “Slaying Sharp.” The abbreviation tan(x) is used by textbooks to stand for what they call 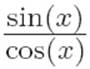, or what we call . See V and H in this dictionary for what textbooks call “sine” and “cosine.”

V

Our name for what textbooks call “sine.” We use this name to stand for the word “vertical.” Used because a straight line tilted at an angle of α will have a vertical length of sin(α), which we instead call V (α). Also see H for what textbooks call “cosine.”

Λ

Our name for what textbooks call “arcsine” or “inverse sine,” and write as either arcsin(x) or sin⁻¹(x), used briefly in Interlude 6, “Slaying Sharp.” We use this name because the Greek letter Λ looks like an upside-down V, and we are using V to stand for what textbooks call “sine” (see V in this dictionary). The machine Λ is defined to satisfy

for all x. However, this machine cannot be defined unambiguously for all numbers x, because V repeats itself (it is not “one to one,” in mathematical jargon). For example, using the standard symbol π to stand for what we have called in this book, we have V (nπ) = 0 for all positive and negative whole numbers n. Because of this, there is no unique number we can choose for Λ(0), because any of the values nπ (e.g., − 2π, −π, 0, π, 2 π, etc.), would appear to be equally valid choices. A common convention that is used to circumvent this problem is simply to define Λ(x) to be the “inverse function” or “opposite machine” not of V(x), but of V(x) restricted to a small subset of the real numbers. For example, it happens to be the case that for , the machine V(x) does not repeat itself; different inputs give different outputs. That is, for all numbers x and y between and, if x ≠ y, then V(x) ≠ V(y). Because of this, Λ is typically defined to be the “inverse function” or “opposite machine” of this restricted version of the machine V. However, this is a fairly boring technical point. We found no need to discuss the topic of “inverse functions” in a general context in this book, except in a few particular cases when the need arose.

⊥

Used briefly in Interlude 6, “Slaying Sharp,” this is our name for what textbooks call “arctangent” or “inverse tangent,” and typically write as either arctan(x) or tan⁻¹(x). We use this name because the symbol ⊥ looks like an upside down T, and we are using T to stand for what textbooks call “tangent” (see T in this dictionary). The machine ⊥ is defined to satisfy

See Sharp.

From Standard Terminology to Our Terminology

Arcsine: See Λ. Also see V for sine.

Arctangent: See ⊥. Also see T for tangent.

Calculus of Variations: See Cannibal Calculus.

Cosine: See H.

Distributive Property: See Obvious Law of Tearing Things.

Function: See Machine.

Functionals: See Cannibalistic Machines.

Hypotenuse: See Shortcut Distance.

Pi (π): See Sharp ().

Polynomials: See Plus-Times Machines.

Pythagorean Theorem: See Formula for Shortcut Distances.

Reciprocal: See Handstand.

Sine: See V.

Tangent: See T.

Taylor Series: See Nostalgia Device.