Calculus II For Dummies, 2nd Edition (2012)

Part VI. The Part of Tens

In this part . . .

As a special bonus, here are two top-ten lists on calculus-related topics: ten important Calculus II “aha” moments and ten useful test-taking tips.

Chapter 16. Ten “Aha!” Insights in Calculus II

In This Chapter

Understanding the key concepts of integration

Distinguishing the definite integral from the indefinite integral

Okay, here you are near the end of the book. You’ve read every single word that I wrote, memorized the key formulas, and worked through all the problems. You’re all set to ace your final exam, and you’ve earned it. Good for you! (Or maybe you just picked up the book and skipped to the end. That’s fine, too! This is a great place to get an overview of what this Calculus II stuff is all about.)

But still, you have this sneaking suspicion that you’re stuck in the middle of the forest and can’t see it because of all those darn trees. Forget the equations for a moment and spend five minutes looking over these top ten “Aha!” insights. When you understand them, you have a solid conceptual framework for Calculus II.

Integrating Means Finding the Area

Finding the area of a polygon or circle is easy. Integration is all about finding the area of shapes with weird edges that are hard to work with. These edges may be the curves that result from polynomials, exponents, logarithms, trig functions, or inverse trig functions, or the products and compositions of these functions.

Integration gives you a concrete way to look at this question, known as the area problem. No matter how complicated integration gets, you can always understand what you’re working on in terms of this simple question: “How does what I’m doing help me find an area?”

See Chapter 1 for more about the relationship between integration and area.

When You Integrate, Area Means Signed Area

In the real world, area is always positive. For example, there’s no such thing as a piece of land that’s –4 square miles in area. This concept of area is called unsigned area.

But on the Cartesian graph in the context of integration, area is measured as signed area, with area below the x-axis considered to be negative area.

In this context, a 2-x-2-unit square below the x-axis is considered to be –4 square units in signed area. Similarly, a 2-x-2-unit square that’s divided in half by the x-axis is considered to have an area of 0.

The definite integral always produces the signed area between a curve and the x-axis, within the limits of integration. So if an application calls for the unsigned area, you need to measure the positive area and negative area separately, change the sign of the negative area, and add these two results together.

See Chapter 3 for more about signed area.

Integrating Is Just Fancy Addition

To measure the area of an irregularly shaped polygon, a good first step is to cut it into smaller shapes that you know how to measure — for example, triangles and rectangles — and then add up the areas of these shapes.

Integration works on the same principle. It allows you to slice a shape into smaller shapes that approximate the area that you’re trying to measure, and then add up the pieces. In fact, the integral sign itself is simply an elongated S, which stands for sum.

See Chapter 1 for more about how integration relates to addition.

Integration Uses Infinitely Many Infinitely Thin Slices

Here’s where integration differs from other methods of measuring area: Integration allows you to slice an area into infinitely many pieces, all of which are infinitely thin, and then add up these pieces to find the total area.

Or, to put a slightly more mathematical spin on it: The definite integral is the limit of the total area of all these slices as the number of slices approaches infinity and the thickness of each slice approaches 0.

This concept is also useful when you’re trying to find volume, as I show you in Chapter 10.

See Chapter 1 for more about how this concept of infinite slicing relates to integration.

Integration Contains a Slack Factor

Math is a harsh mistress. A small error at the beginning of a problem often leads to a big mistake by the end.

So finding out that you can thin-slice an area in a bunch of different ways and still get the correct answer is refreshing. Some of these methods for thin-slicing include left rectangles, right rectangles, and midpoint rectangles. I cover them all in Chapter 3.

This slack factor, as I call it, comes about because integration exploits an infinite sequence of successive approximations. Each approximation brings you closer to the answer that you’re seeking. So no matter what route you take to get there, an infinite number of such approximations brings you to the answer.

See Chapter 3 for more about the distinction between approximating and evaluating integrals.

A Definite Integral Evaluates to a Number

A definite integral represents the well-defined area of a shape on a graph. You can represent any such area as a number of square units, so the definite integral is a number.

See Chapter 3 for more about the definite integral.

An Indefinite Integral Evaluates to a Function

An indefinite integral is a template that allows you to calculate an infinite number of related definite integrals by plugging in some parameters. In math, such a template is called a function.

The input values to an indefinite integral are the two limits of integration. Specifying these two values turns the indefinite integral into a definite integral, which then outputs a number representing an area.

But if you don’t specify the limits of integration, you can still evaluate an indefinite integral as a function. The process of finding an indefinite integral turns an input function (for example, cos x) into an output function (sin x + C).

See Chapter 3 for more about the indefinite integral and Part II for a variety of techniques for evaluating indefinite integrals.

Integration Is Inverse Differentiation

Integration and differentiation are inverse operations: Either of these operations undoes the other (up to a constant C). Another way to say this is that integration is anti-differentiation.

Here’s an example of how differentiation undoes integration:

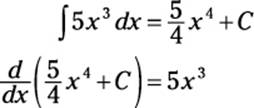
As you can see, integrating a function and then differentiating the result produces the function that you started with.

Now here’s an example of how integration undoes differentiation:

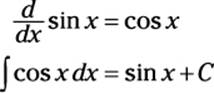
As you can see, differentiating a function and then integrating the result produces the function that you started with, plus a constant C.

See Part II for more on how this inverse relationship between integration and differentiation provides a variety of clever methods for integrating complicated functions.

Every Infinite Series Has Two Related Sequences

Every infinite series has two related sequences that are important for understanding how that series works: its defining sequence and its sequence of partial sums.

The defining sequence of a series is simply the sequence that defines the series in the first place. For example, the series

has the defining sequence

Notice that the same function — in this case, — appears in the shorter notation for both the series and its defining sequence.

The sequence of partial sums of a series is the sequence that results when you successively add a finite number of terms. For example, the previous series has the following sequence of partial sums:

Notice that a series may diverge while its defining sequence converges, as in this example. However, a series and its sequence of partial sums always converge or diverge together. In fact, the definition of convergence for a series is based on the behavior of its sequence of partial sums (see the next section for more on convergence and divergence).

See Part IV for more about infinite series.

Every Infinite Series Either Converges or Diverges

Every infinite series either converges or diverges, with no exceptions.

A series converges when it evaluates to (equals) a real number. For example:

On the other hand, a series diverges when it doesn’t evaluate to a real number. Divergence can happen in two different ways. The more common type of divergence is when the series explodes to ∞ or –∞. For example:

Clearly, this series doesn’t add up to a real number — it just keeps getting bigger and bigger forever.

Another type of divergence occurs when a series bounces forever among two or more values. This happens only when a series is alternating (see Chapter 12 for more on alternating series). For example:

The sequence of partial sums (see the previous section) for this series alternates forever between –1 and 0, never settling in to a single value, so the series diverges.

See Part IV for more about infinite series.