Calculus For Dummies, 2nd Edition (2014)

Part V. Integration and Infinite Series

Chapter 18. Taming the Infinite with Improper Integrals

IN THIS CHAPTER

The hospital rule — in case studying calculus makes you ill

Meeting integrals without manners

The paradox of Gabriel’s horn

In Chapter 17, you used down-to-earth integrals to compute some relatively ordinary things like the area between curves, the volumes of 3-D shapes, the lengths of curves, etc. I say these things are down-to-earth because all of them involved finite things — things with a beginning and an end, things (like a bowl-shaped 3-D object) that you could sort of hold in your hand. In this chapter, you enter the twilight zone of integrals that go to infinity. These are fascinating problems that often have surprising results. But first, we have to take care of L’Hôpital’s rule — a handy technique to put into your calculus bag of tricks.

L’Hôpital’s Rule: Calculus for the Sick

L’Hôpital’s rule is a great shortcut for doing limit problems. Remember limits — from way back in Chapters 7 and 8 — like ? By the way, if you’re wondering why I’m showing you this limit shortcut now, it’s because (a) you may need it someday to solve some improper integral problems (the topic of the next section in this chapter), though we don’t do such an example, and (b) you also need it for some of the infinite series problems in Chapter 19.

As with most limit problems — not counting no-brainer problems — you can’t do with direct substitution: plugging 3 into x gives you , which is undefined. In Chapter 8, you learned to do this problem by factoring the numerator into and then canceling the . That left you with , which equals 6.

Now watch how easy it is to take the limit with L’Hôpital’s rule. Simply take the derivative of the numerator and the derivative of the denominator. Don’t use the quotient rule; just take the derivatives of the numerator and denominator separately. The derivative of is 2x and the derivative of is 1. L’Hôpital’s rule lets you replace the numerator and denominator by their derivatives like this:

The new limit is a no-brainer:

That’s all there is to it. L’Hôpital’s rule transforms a limit you can’t do with direct substitution into one you can do with substitution. That’s what makes it such a great shortcut.

Here’s the mumbo jumbo.

L’Hôpital’s rule: Let f and g be differentiable functions. If the limit of as x approaches c produces when you substitute the value of c into x, then

Note that c can be a number or . And note that in the over case, both infinities can be of the same sign or one can be positive and the other negative.

Here’s an example involving : What’s ? Direct substitution gives you , so you can use L’Hôpital’s rule. The derivative of is , and the derivative of x is 1, so

Try another one: Evaluate . Substitution gives you so L’Hôpital’s rule applies. The derivative of is and the derivative of x is 1, thus

You must have zero over zero or infinity over infinity. The mumbo jumbo says that to use L’Hôpital’s rule, substitution must produce either . You must get one of these acceptable “indeterminate” forms in order to apply the shortcut. Don’t forget to check this.

Getting unacceptable forms into shape

If substitution produces one of the unacceptable forms, or , you first have to tweak the problem to get an acceptable form before using L’Hôpital’s rule.

For instance, find . Substituting infinity into x gives you so you’ve got to tweak it:

Now you’ve got the case, so you’re all set to use L’Hôpital’s rule. The derivative of is , and the derivative of is , so

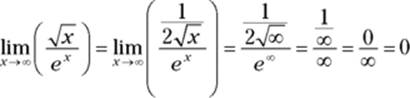
Here’s another problem: What’s ? (Recall from Chapter 7 that means that x approaches 0 from the right only; this is a one-sided limit.) First, substitute zero into x (actually, since x is approaching zero from the right, you must imagine plugging a tiny positive number into x, or you can sort of think of it as plugging a “positive” zero into x). Substitution gives you , which results in , one of the unacceptable forms. So tweak the limit expression with some algebra:

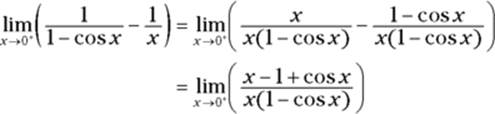
Now substitution gives you , so you can finish with L’Hôpital’s rule:

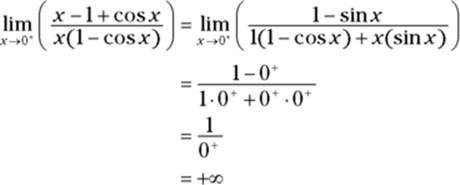
That’s it.

Three more unacceptable forms

When substitution of the arrow-number into the limit expression produces one of the unacceptable forms , or , you use the following logarithm trick to turn it into an acceptable form. Here’s how it works. Let’s find . Substitution gives you , which equals , so you do the following:

1. Set the limit equal to y.

2. Take the log of both sides.

3. This limit is a case, so tweak it.

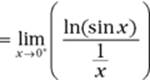
4. Now you’ve got a case, so you can use L’Hôpital’s rule.

The derivative of is , or , and the derivative of is , so

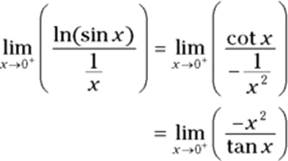
5. This is a case, so use L’Hôpital’s rule again.

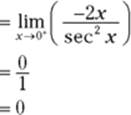
Hold your horses! This is not the answer.

6. Solve for y.

Do you see that the answer of 0 in Step 5 is the answer to the equation from way back in Step 2: ? So, the 0 in Step 5 tells you that . Now solve for y:

Because you set your limit equal to y in Step 1, this, finally, is your answer:

Ordinary math doesn’t work with infinity (or zero to the zero power). Don’t make the mistake of thinking that you can use ordinary arithmetic or the laws of exponents when dealing with any of the acceptable or unacceptable indeterminate forms. It might look like should equal zero, for example, but it doesn’t. By the same token, , , , , , and .

Improper Integrals: Just Look at the Way That Integral Is Holding Its Fork!

Definite integrals are improper when they go infinitely far up, down, right, or left. They go up or down infinitely far in problems like that have one or more vertical asymptotes. They go infinitely far to the right or left in problems like or , where one or both of the limits of integration are infinite. (There are a couple other weird types of improper integrals, but they’re rare — don’t worry about them.) It would seem to make sense to just use the term infinite instead of improper to describe these integrals, except for the remarkable fact that many of these “infinite” integrals give you a finite area. More about this in a minute.

You solve both types of improper integrals by turning them into limit problems. Take a look at some examples.

Improper integrals with vertical asymptotes

There are two cases to consider here: problems where there’s a vertical asymptote at one of the edges of the area in question and problems where there’s a vertical asymptote somewhere in the middle of the area.

A vertical asymptote at one of the limits of integration

What’s the area under from 0 to 1? This function is undefined at , and it has a vertical asymptote there. So you’ve got to turn the definite integral into a limit where c approaches the x-value of the asymptote:

This area is infinite, which probably doesn’t surprise you because the curve goes up to infinity. But hold on to your hat — the next function also goes up to infinity at , but its area is finite!

Find the area under from 0 to 1. This function is also undefined at , so the process is the same as in the previous example:

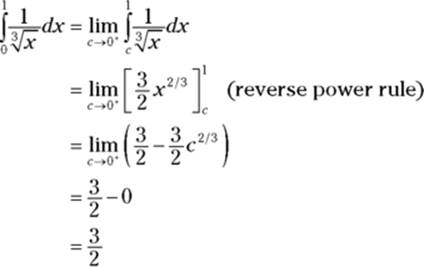
Convergence and divergence: You say that an improper integral converges if the limit exists — that is, if the limit equals a finite number like in the second example. Otherwise, an improper integral is said to diverge— like in the first example. When an improper integral diverges, the area in question (or part of it) usually (but not always) equals .

A vertical asymptote between the limits of integration

If the undefined point of the integrand is somewhere in between the limits of integration, you split the integral in two — at the undefined point — then turn each integral into a limit and go from there. Evaluate . This integrand is undefined at .

1. Split the integral in two at the undefined point.

2. Turn each integral into a limit and evaluate.

For the integral, the area is to the left of zero, so c approaches zero from the left. For the integral, the area is to the right of zero, so c approaches zero from the right.

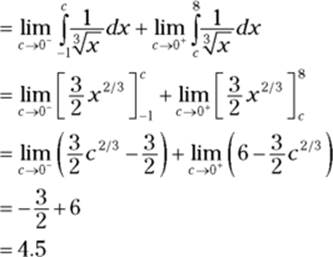
Keep your eyes peeled for x-values where an integrand is undefined. If you fail to notice that an integrand is undefined at an x-value between the limits of integration, and you integrate the ordinary way, you may get the wrong answer. The above problem, (undefined at ), happens to work out correctly if you do it the ordinary way. However, if you do (also undefined at ) the ordinary way, not only do you get the wrong answer, you get the totally absurd answer of negative 2, despite the fact that the area in question is above the x-axis and is therefore a positive area. The moral: Don’t risk it.

If a part diverges, the whole diverges. If either part of the split up integral diverges, the original integral diverges. You can’t get, say, for one part and for the other part and add them up to get zero.

Improper integrals with one or two infinite limits of integration

You do these improper integrals by turning them into limits where c approaches infinity or negative infinity. Two examples: and .

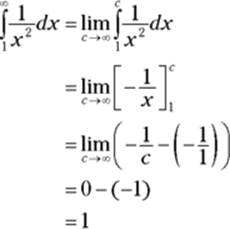
So this improper integral converges.

In the next integral, the denominator is smaller, x instead of , and thus the fraction is bigger, so you’d expect to be bigger than , which it is. But it’s not just bigger, it’s way bigger:

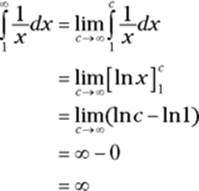
This improper integral diverges.

Figure 18-1 shows these two functions. The area under from 1 to is exactly the same as the area of the 1-by-1 square to its left: 1 square unit. The area under from 1 to is much, much bigger — actually, it’s infinitely bigger than a square large enough to enclose the Milky Way Galaxy. Their shapes are quite similar, but their areas couldn’t be more different.

FIGURE 18-1: The area under from 1 to and the area under from 1 to .

By the way, these two functions make another appearance in Chapter 19 on infinite series. Deciding whether an infinite series converges or diverges — a distinction quite similar to the difference between these two functions — is one of the main topics in Chapter 19.

When both of the limits of integration are infinite, you split the integral in two and turn each part into a limit. Splitting up the integral at is convenient because zero’s an easy number to deal with, but you can split it up anywhere you like. Zero may also seem like a good choice because it looks like it’s in the middle between and . But that’s an illusion because there is no middle between and , or you could say that any point on the x-axis is the middle.

Here’s an example:

1. Split the integral in two.

2. Turn each part into a limit.

3. Evaluate each part and add up the results.

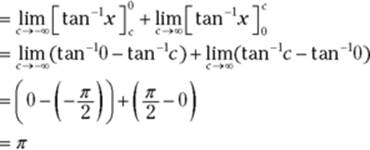
Why don’t you do this problem again, splitting up the integral somewhere other than at , to confirm that you get the same result.

If either “half” integral diverges, the whole, original integral diverges.

Blowing Gabriel’s horn

This horn problem may blow your mind.

Gabriel’s horn is the solid generated by revolving about the x-axis the unbounded region between and the x-axis (for ). See Figure 18-2. Playing this instrument poses several not-insignificant challenges: 1) It has no end for you to put in your mouth; 2) Even if it did, it would take you till the end of time to reach the end; 3) Even if you could reach the end and put it in your mouth, you couldn’t force any air through it because the hole is infinitely small; 4) Even if you could blow the horn, it’d be kind of pointless because it would take an infinite amount of time for the sound to come out. There are additional difficulties — infinite weight, doesn’t fit in universe, and so on — but I suspect you get the picture.

FIGURE 18-2: Gabriel’s horn.

Believe it or not, Gabriel’s horn has a finite volume, but an infinite surface area! You use the disk method to figure its volume (see Chapter 17). Recall that the volume of each representative disk is . For this problem, the radius is , so the little bit of volume is . You find the total volume by adding up the little bits from 1 to

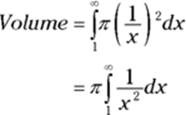
In the section on improper integrals, we calculated that , so the volume is , or just .

To determine the surface area, you first need the function’s derivative (the method for calculating surface area is covered in the “Surfaces of Revolution” section in Chapter 17):

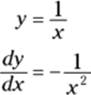
Now plug everything into the surface area formula:

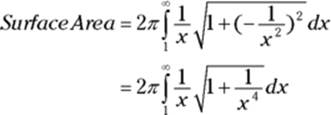
In the previous section, we determined that , and because is always greater than in the interval , must also equal . Finally, times is still , of course, so the surface area is infinite.

Bonus question for those with a philosophical bent: Assuming Gabriel is omnipotent, could he overcome the above-mentioned difficulties and blow this horn? Hint: All the calculus in the world won’t help you with this one.