The Calculus Primer (2011)
Part IX. Indeterminate Forms
Chapter 33. THEOREM OF MEAN VALUE
9—1.Rolle’s Theorem. Let us consider a continuous single-valued function y = f(x), with zero-values at x = a and x = b. Let us assume that f′(x) changes continuously as x varies from a to b. From the figure, by Intuition, it is clear that for at least one value of x between a and b the tangent to the curve must be parallel to the X-axis, as at P or Q; that is, the slope of the curve is zero for at least one value between x = a and x = b.
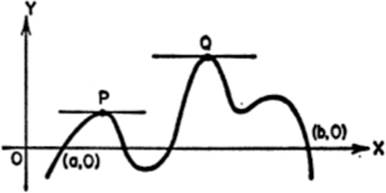
This principle may be stated without formal proof as Rolle’s Theorem, as follows:
If f(x) = 0 when x = a and when x = b, and if both f(x) and f′(x) are continuous for all values of x from x = a to x = 6, then f′(x) will equal zero for at least one value of x between a and b.
What this means is that, as x increases from a to b, f(x) cannot always increase, since f(a) = f(b) = 0; similarly, f(x) cannot always decrease as x increases from a to b. Therefore, for at least one value of x between a and 6, f(x) must stop increasing and begin to decrease, or stop decreasing and begin to increase. We have already learned that at a turning point in a curve, the value of f′(x) is zero.
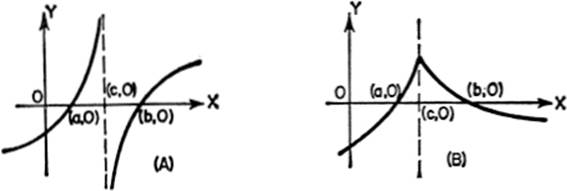
From a consideration of the following figures, it will be seen that Rolle’s Theorem does not hold if either f(x) or f′(x) is discontinuous. Thus in (A) the function is discontinuous at x = c; in (B), the first derivative is discontinuous at x = c. In both cases there is no point on the curve between x = a and x = b at which the tangent becomes parallel to the X-axis.
9—2.Multiple Roots of an Equation. In algebra it is shown that if f(x) is a polynomial function, and f(a) and f(b) are opposite in sign, then an odd number of roots of f(x) = 0 will lie between a and b; if f(a) and f(b) have the same sign, either no root, or an even number of roots, will lie between a and b.
It is also shown in algebra that if the equation f(x) = 0 has r roots equal to a, then the equation f′(x) = 0 will have (r − 1) roots equal to a. This is another way of saying that if f(x) contains a factor (x − a)r, then the equation f′(x) = 0 will have (r − 1) roots equal to a; in short, f(x) and f′(x) have a common factor (x − a)r−1. Thus an equation f(x) = 0 has or has not equal roots, according as f(x) and f′(x) have or do not have a common factor involving x. Such equal roots are also called multiple roots of an equation. To determine whether or not an equation has multiple roots, it is only necessary to determine whether f(x) and f′(x) have a common factor.
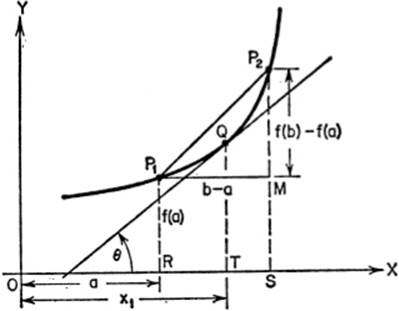
9—3.The Mean Value Theorem. The principle of Rolle’s Theorem can be formulated analytically as follows. Let the abscissas of P1 and P2 be a and b, respectively; then RP1 = f(a), SP2 = f(b), and MP2 = f(b) − f(a). The slope of the line P1P2 is seen to be
![]()
Now let us denote this last fraction by the symbol Q, that is, let
![]()
Clearing of fractions:
f(b) − f(a) − (b − a)Q = 0.(2)
Let ø(x) be a function formed by replacing b by x in equation (2):
ø(x) = f(x) −(a) − (x − a)Q.(3)
From equation (2), we find ø(b) = 0; and from equation (3), we find ø(a) = 0. Therefore, from Rolle’s Theorem, ø′(x) must vanish for at least one value of x between a and b; call this value x1. By differentiating equation (3):
ø′(x) = f′(x) − Q.(4)
Butø′(x1) = 0;
hencef′(x1) − Q = 0,
orQ = f′(x1).(5)
Substituting from equation (5) in equation (1):
![]()
where a < x1 < b.
Referring now to the first paragraph of §9—3, we see that there is at least one point on the curve between P1 and P2 where the tangent to the curve is parallel to the chord P1P2. If the abscissa of this point is called x1, then the slope at that point is given by
tan MP1P2 = tan θ = f′(x1) = ![]() .
.
![]()
orf(b) = f(a) + (b − a)f–(x1),[2]
where x1 lies between a and b. Equations [1] and [2] are alternative forms of stating the law of the mean, or the mean value theorem. It is a principle which has many uses in the calculus.