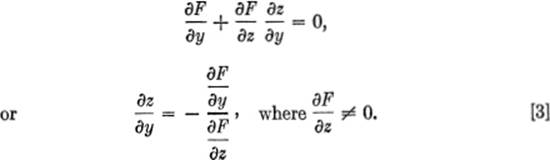The Calculus Primer (2011)

Part X. Partial Differentiation

Chapter 36. THE TOTAL DERIVATIVE

10—4.Tolal Differential. We have already learned how to find the derivative of a function of a function; thus, if y = f(u), and u = F(x), then

In a similar way, it may be shown that if z = f(x,y), and x = F₁ (t) and y = F₂(t) then

Equation [1] gives the total derivative of z with respect to t. In the same way, if u = f(x,y,z), and x, y, and z are functions of t, then

It should be understood that the meanings of and are definitely different. Thus the partial derivative supposes that only the particular variable x varies; on the other hand, is the limit of , where Δu is the total increment in u brought about by changes in all the variables due to an increment in the independent variable x.

If we multiply equations [1] and [2], respectively, by dt, we obtain

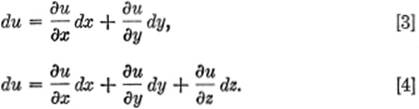
The expression du is called the total differential of u, or the “complete differential.”

The expressions dx, dy, etc. are called partial differentials.

10—5.Implicit Functions. The expression f(x,y) = 0 represents an equation in x and y where all the terms have been transposed to one side of the equation. In other words, y is an implicit function of x (or x is an implicit function of y). Now, let us set z = f(x,y), and find the total differential of z; from [3], §10—4, we have:

But by hypothesis, since z = f(x,y) = 0, then for all values of x, z = 0; hence dz = 0. Therefore, if ≠ 0:

or, dividing (2) through by dx and by , we get:

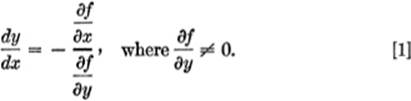
EXAMPLE. If f(x,y) = x² + y³ + xy = 0, find by using partial derivatives.

Solution.

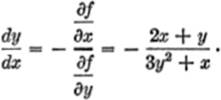
This result agrees, of course, with the value of found by the previously learned method; thus, differentiating “directly”:

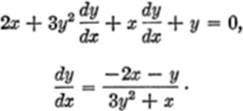
The relation above is quite general. Thus if

u = F(x,y,z) = 0,

then, by §10—4, equation [4]:

Analogous to the derivation in the earlier part of the present section, we remember that z is a function of x and y, so that

Substituting the value of dz from (2) in equation (1), and remembering that du = 0, we obtain:

or, by factoring:

Since z is a function of x and y, the variables x and y are independent variables, and so we may assign to the increments dx and dy such values as we please.

Let us first set dy = 0, ≠ 0; then, from (3), we get:

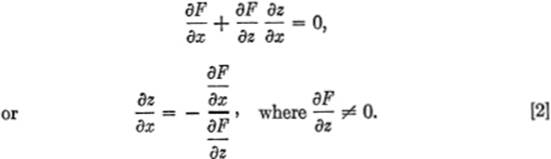
Next, we set dx = 0, dy ≠ 0; then, from (3) we get: