Easy Algebra Step-by-Step: Master High-Frequency Concepts and Skills for Algebra Proficiency—FAST! (2012)
Chapter 13. Rational Expressions
In this chapter, you apply your skills in factoring polynomials to the charge of simplifying rational expressions. A rational expression is an algebraic fraction that has a polynomial for its numerator and a polynomial for its denominator. For instance, ![]() is a rational expression. Because division by 0 is undefined, you must exclude values for the variable or variables that would make the denominator polynomial sum to 0. For convenience, you can assume such values are excluded as you work through the problems in this chapter.
is a rational expression. Because division by 0 is undefined, you must exclude values for the variable or variables that would make the denominator polynomial sum to 0. For convenience, you can assume such values are excluded as you work through the problems in this chapter.
Reducing Algebraic Fractions to Lowest Terms
The following principle is fundamental to rational expressions.
![]() Fundamental Principle of Rational Expressions
Fundamental Principle of Rational Expressions
If P, Q, and R are polynomials, then ![]() , provided neither Q nor R has a zero value.
, provided neither Q nor R has a zero value.
The fundamental principle allows you to reduce algebraic fractions to lowest terms by dividing the numerator and denominator by the greatest common factor (GCF).
Before applying the fundamental principle of rational expressions, always make sure that the numerator and denominator contain only factored polynomials.
Problem Reduce to lowest terms.
a. ![]()
b. ![]()
c. ![]()
d. ![]()
e. ![]()
f. ![]()
g. ![]()
Solution
a. ![]()
![]() Step 1. Determine the GCF for
Step 1. Determine the GCF for ![]() and
and ![]()
![]()
Step 2. Write the numerator and denominator as equivalent products with the GCF as one of the factors.
![]()
Step 3. Use the fundamental principle to reduce.
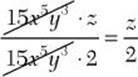
b. ![]()
![]() Step 1. Determine the GCF for 6x and 2x.
Step 1. Determine the GCF for 6x and 2x.
GCF = 2x
Step 2. Write the numerator and denominator as equivalent products with the GCF as one of the factors.
![]()
Step 3. Use the fundamental principle to reduce the fraction.
![]()
c. ![]()
![]() Step 1. Factor –1 from the denominator polynomial, so that the x term will have a positive coefficient.
Step 1. Factor –1 from the denominator polynomial, so that the x term will have a positive coefficient.
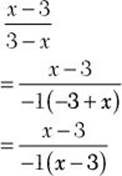
Step 2. Determine the GCF for x –3 and –1(x – 3).
GCF = (x – 3) (Enclose x – 3 in parentheses to emphasize it’s a factor.)
Step 3. Write the numerator and denominator as equivalent products with the GCF as one of the factors.
![]()
Step 4. Use the fundamental principle to reduce the fraction.
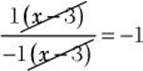
![]() . Think of (x –3) as 1(x –3)
. Think of (x –3) as 1(x –3)
d. ![]()
![]() Step 1. Determine the GCF for 3x and 3 + x.
Step 1. Determine the GCF for 3x and 3 + x.
GCF = 1, so ![]() cannot be reduced further.
cannot be reduced further.
![]() . 3 is a factor of the numerator, but it is a term of the denominator. It is a mistake to divide out a term.
. 3 is a factor of the numerator, but it is a term of the denominator. It is a mistake to divide out a term.
e. ![]()
![]() Step 1. Factor the numerator and denominator polynomials completely.
Step 1. Factor the numerator and denominator polynomials completely.
![]()
Step 2. Determine the GCF for ![]() and
and ![]()
![]()
Step 3. Use the fundamental principle to reduce the fraction.
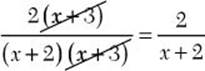
![]() . 6 is a common term in the numerator and denominator, not a factor. Only divide out factors.
. 6 is a common term in the numerator and denominator, not a factor. Only divide out factors.
f. ![]()
![]() Step 1. Factor the numerator and denominator polynomials completely.
Step 1. Factor the numerator and denominator polynomials completely.
![]()
Step 2. Determine the GCF for ![]() and
and ![]()
![]()
Step 3. Write the numerator and denominator as equivalent products with the GCF as one of the factors.
![]()
Step 4. Use the fundamental principle to reduce the fraction.
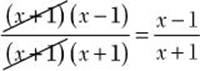
g. ![]()
![]() Step 1. Factor the numerator and denominator polynomials completely.
Step 1. Factor the numerator and denominator polynomials completely.
![]()
Step 2. Determine the GCF for ![]() and
and ![]()
![]()
Step 3. Use the fundamental principle to reduce the fraction.
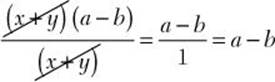
Multiplying Algebraic Fractions
To multiply algebraic fractions, (1) factor all numerators and denominators completely, (2) divide numerators and denominators by their common factors (as in reducing), and (3) multiply the remaining numerator factors to get the numerator of the answer and multiply the remaining denominator factors to get the denominator of the answer.
Problem Find the product.
a. ![]()
b. ![]()
Solution
a. ![]()
![]() Step 1. Factor all numerators and denominators completely.
Step 1. Factor all numerators and denominators completely.
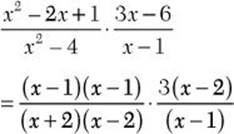
When you are multiplying algebraic fractions, if a numerator or denominator does not factor, enclose it in parentheses. Forgetting the parentheses can lead to a mistake.
Step 2. Divide out common numerator and denominator factors.
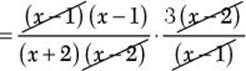
Be careful! Only divide out factors.
Step 3. Multiply the remaining numerator factors to get the numerator of the answer and multiply the remaining denominator factors to get the denominator of the answer.
![]()
Step 4. Review the main results.
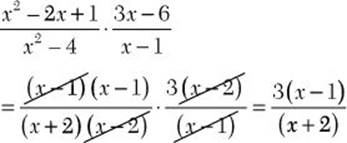
When you multiply algebraic fractions, you can leave your answer in factored form. Always double-check to make sure it is in completely reduced form.
b. ![]()
![]() Step 1. Factor all numerators and denominators completely.
Step 1. Factor all numerators and denominators completely.
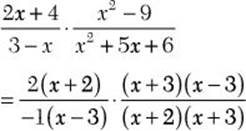
Write all polynomial factors with the variable terms first, so that you can easily recognize common factors.
Step 2. Divide out common numerator and denominator factors.
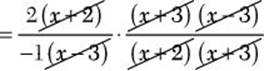
Step 3. Multiply the remaining numerator factors to get the numerator of the answer, and multiply the remaining denominator factors to get the denominator of the answer.
![]()
Step 4. Review the main results.
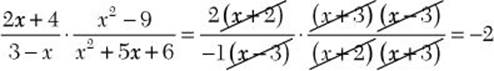
Dividing Algebraic Fractions
To divide algebraic fractions, multiply the first algebraic fraction by the reciprocal of the second algebraic fraction (the divisor).
Problem Find the quotient: ![]()
Solution
![]() Step 1. Change the problem to multiplication by the reciprocal of the divisor.
Step 1. Change the problem to multiplication by the reciprocal of the divisor.
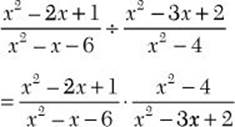
Step 2. Factor all numerators and denominators completely.
![]()
Step 3. Divide out common numerator and denominator factors.
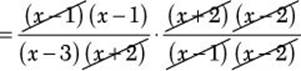
Step 4. Multiply the remaining numerator factors to get the numerator of the answer, and multiply the remaining denominator factors to get the denominator of the answer.
![]()
Step 5. Review the main results.
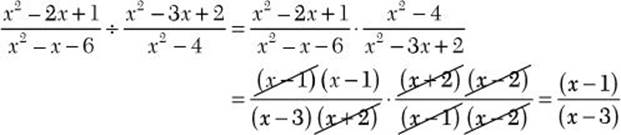
Adding (or Subtracting) Algebraic Fractions, Like Denominators
To add (or subtract) algebraic fractions that have like denominators, place the sum (or difference) of the numerators over the common denominator. Simplify and reduce to lowest terms, if needed.
Problem Compute as indicated.
a. ![]()
b. ![]()
Solution
a. ![]()
![]() Step 1. Indicate the sum of the numerators over the common denominator.
Step 1. Indicate the sum of the numerators over the common denominator.
![]()
![]()
Step 2. Find the sum of the numerators.
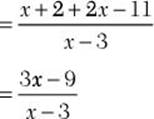
Step 3. Reduce to lowest terms.
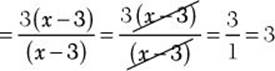
Step 4. Review the main results.
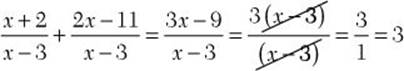
b. ![]()
![]() Step 1. Indicate the difference of the numerators over the common denominator.
Step 1. Indicate the difference of the numerators over the common denominator.
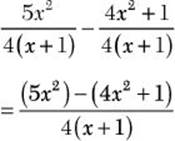
When subtracting algebraic fractions, it is important that you enclose the numerator of the second fraction in parentheses because you want to subtract the entire numerator, not just the first term.
Step 2. Find the difference of the numerators.
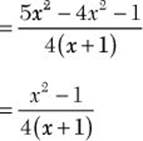
Step 3. Reduce to lowest terms.
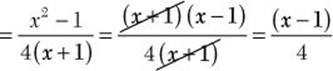
Step 4. Review the main results.
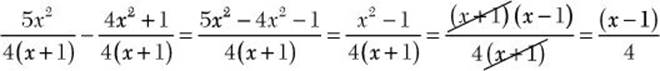
Adding (or Subtracting) Algebraic Fractions, Unlike Denominators
To add (or subtract) algebraic fractions that have unlike denominators, (1) factor each denominator completely; (2) find the least common denominator (LCD), which is the product of each prime factor the highest number of times it is a factor in any one denominator; (3) using the fundamental principle, write each algebraic fraction as an equivalent fraction having the common denominator as a denominator; and (4) add (or subtract) as for like denominators.
Note: A prime factor is one that cannot be factored further.
Problem Compute as indicated.
a. ![]()
b. ![]()
Solution
a. ![]()
![]() Step 1. Factor each denominator completely.
Step 1. Factor each denominator completely.
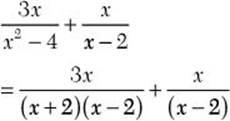
Step 2. Find the LCD.
LCD = (x + 2) (x –2)
Step 3. Write each algebraic fraction as an equivalent fraction having the common denominator as a denominator.
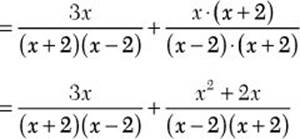
Step 4. Add as for like denominators.
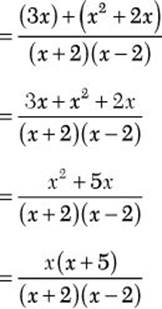
Step 5. Review the main results.
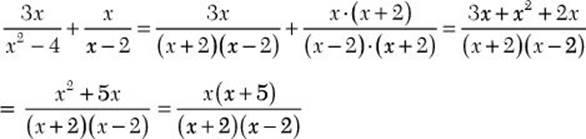
b. ![]()
![]() Step 1. Factor each denominator completely.
Step 1. Factor each denominator completely.
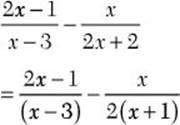
Step 2. Find the LCD.
LCD = 2(x –3)(x + 1)
Step 3. Write each algebraic fraction as an equivalent fraction having the common denominator as a denominator.
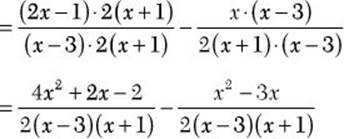
Step 4. Subtract as for like denominators.
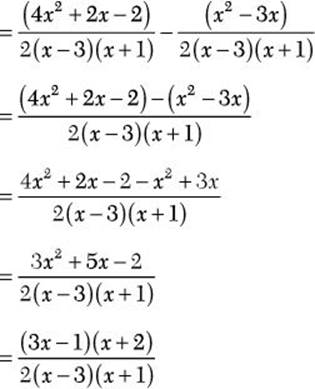
Step 5. Review the main results.
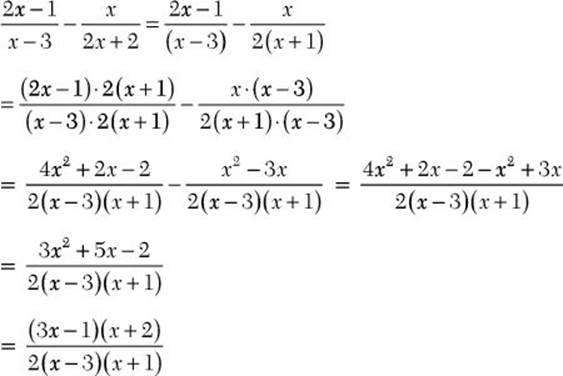
Complex Fractions
A complex fraction is a fraction that has fractions in its numerator, denominator, or both. One way you can simplify a complex fraction is to interpret the fraction bar of the complex fraction as meaning division.
Problem Simplify 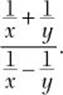
Solution
![]() Step 1. Write the complex fraction as a division problem.
Step 1. Write the complex fraction as a division problem.
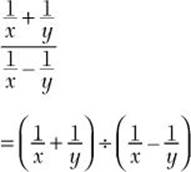
Step 2. Perform the indicated addition and subtraction.
![]()
Step 3. Multiply by the reciprocal of the divisor.
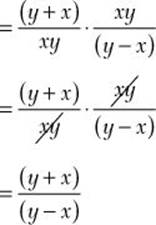
Step 4. Review the main results.
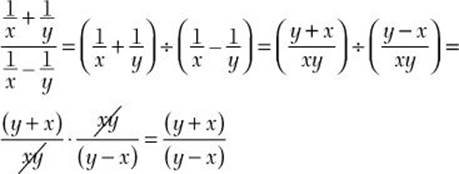
Another way you can simplify a complex fraction is to multiply its numerator and denominator by the LCD of all the fractions in its numerator and denominator.
Problem Simplify: 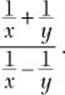
Solution
![]() Step 1. Multiply the numerator and denominator by the LCD of all the fractions.
Step 1. Multiply the numerator and denominator by the LCD of all the fractions.
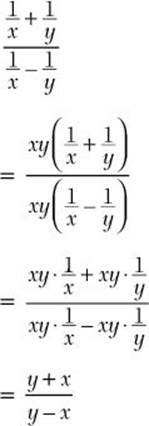
![]() Exercise 13
Exercise 13
For 1–10, reduce to lowest terms.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
For 11–15, compute as indicated.
11. ![]()
12. ![]()
13. ![]()
14. ![]()
15. ![]()