What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

§2. INCOMMENSURABLE SEGMENTS, IRRATIONAL NUMBERS, AND THE CONCEPT OF LIMIT

1. Introduction

In comparing the magnitudes of two line segments a and b, it may happen that a is contained in b an exact integral number r of times. In this case we can express the measure of the segment b in terms of that of a by saying that the length of b is r times that of a. Or it may turn out that while no integral multiple of a equals b, we can divide a into, say, n equal segments, each of length a/n, such that some integral multiple m of the segment a/n is equal to b:

(1)  

When an equation of the form (1) holds we say that the two segments a and b are commensurable, since they have as a common measure the segment a/n which goes n times into a and m times into b. The totality

Fig. 9. Rational points.

of all segments commensurable with a will be those whose length can be expressed in the form (1) for some choice of integers m and n (n ≠ 0). If we choose a as the unit segment, [0, 1], in Figure 9, then the segments commensurable with the unit segment will correspond to all the rational points m/n on the number axis. For all practical purposes of measuring, the rational numbers are entirely sufficient. Even from a theoretical viewpoint, since the set of rational points covers the line densely, it might seem that all points on the line are rational points. If this were true, then any segment would be commensurable with the unit. It was one of the most surprising discoveries of early Greek mathematics (the Pythagorean school) that the situation is by no means so simple. There exist incommensurable segments or, if we assume that to every segment corresponds a number giving its length in terms of the unit, irrational numbers. This revelation was a scientific event of the highest importance. Quite possibly it marked the origin of what we consider to be the specifically Greek contribution to rigorous procedure in mathematics. Certainly it has profoundly affected mathematics and philosophy from the time of the Greeks to the present day.

Eudoxus’ theory of incommensurables, presented in geometrical form in Euclid’s Elements, is a masterpiece of Greek mathematics, though it is usually omitted from the diluted high-school versions of this classical work. The theory became fully appreciated only in the late nineteenth century, after Dedekind, Cantor, and Weierstrass had constructed a rigorous theory of irrational numbers. We shall present the theory in the modern arithmetical way.

First we show: The diagonal of a square is incommensurable with its side. We may suppose that the side of the given square is chosen as the unit of length, and that the diagonal has the length x. Then, by the Pythagorean theorem, we have

x² = 1² + 1² = 2.

(We may denote x by the symbol .) Now if x were commensurable with 1, we could find two integers p and q such that x = p/q and

(2) p² = 2q².

We may suppose that p/q is already in lowest terms, since any common factor in numerator and denominator could be cancelled out at the beginning. Since 2 appears as a factor of the right side, p² is an even number, and hence p itself is even, because the square of an odd number is odd. We may therefore write p = 2r. Equation (2) then becomes

4r² = 2q², or 2r² = q².

Since 2 is a factor of the left side, q², and hence q must also be even. Thus p and q are both divisible by 2, which contradicts the assumption that p and q had no common factor. Therefore, equation (2) cannot hold, and x cannot be a rational number.

Our result can be expressed by the statement that there is no rational number equal to

The argument of the preceding paragraph shows that a very simple geometrical construction may result in a segment incommensurable with the unit. If such a segment is marked off on the number axis by means of a compass, the point so constructed cannot coincide with any of the

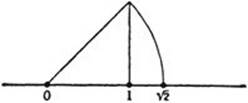
Fig. 10. Construction of .

rational points: The system of rational points, although it is everywhere dense, does not cover all of the number axis. To the naive mind it must certainly appear very strange and paradoxical that the dense set of rational points does not cover the whole line. Nothing in our “intuition” can help us to “see” the irrational points as distinct from the rational ones. No wonder that the discovery of the incommensurable stirred the Greek philosophers and mathematicians, and that it has retained even today its provocative effect on thoughtful minds.

It would be very easy to construct as many segments incommensurable with the unit as we want. The end-points of such segments, if marked off from the point 0 on the number axis, are called irrational points. Now, the guiding principle in introducing fractions was the measuring of lengths by numbers, and we should like to maintain this principle in dealing with segments incommensurable with the unit. If we demand that there should be a mutual correspondence between numbers on the one hand and points of a straight line on the other, it is necessary to introduceirrational numbers.

Summarizing the situation thus far we may say that an irrational number represents the length of a segment incommensurable with the unit. In the following sections we shall refine this somewhat vague and entirely geometrical definition, until we arrive at one more satisfactory from the point of view of logical rigor. Our first approach to the subject will be by way of the decimal fractions.

Exercises: 1) Prove that are not rational. (Hint: Use the lemma of p. 47).

2) Prove that and are not rational. (Hint: If e.g. the first of these numbers were equal to a rational number r then, writing and squaring, would be rational.)

3) Prove that is irrational. Try to make up similar and more general examples.

2. Decimal Fractions. Infinite Decimals

In order to cover the number axis with a set of points everywhere dense, we do not need the totality of all rational numbers; for example, it suffices to consider only those numbers which originate by subdivision of each unit interval into 10, then 100, 1000, etc. equal segments. The points so obtained correspond to the “decimal fractions.” For example, the point 0.12 = 1/10 + 2/100 corresponds to the point lying in the first unit interval, in the second subinterval of length 10^-1, and at the initial point of the third “sub-sub-” interval of length 10^-2. (a^–n means 1/aⁿ.) Such a decimal fraction, if it contains n digits after the decimal point, has the form

f = z + a₁10⁻¹ + a₂10⁻² + a₃10⁻² + · · · + a_n10⁻ⁿ,

where z is an integer and the a’s are digits—0, 1, 2, · · ·, 9—indicating the tenths, hundredths and so on. The number f is represented in the decimal system by the abbreviated symbol z. a₁a₂a₃ · · · a_n. We see immediately that these decimal fractions can be written in the ordinary form of a fraction p/q where q= 10ⁿ; for example, f = 1.314 = 1 + 3/10 + 1/100 + 4/1000 = 1314/1000. If p and q have a common divisor, the decimal fraction may then be reduced to a fraction with a denominator which is some divisor of 10ⁿ. On the other hand, no fraction in lowest terms whose denominator is not a divisor of some power of 10 can be represented as a decimal fraction. For example, and but cannot be written as a decimal fraction with a finite number n of decimal places, however great n be chosen, for an equation of the form

would imply

10ⁿ = 3b,

which is absurd, since 3 is not a factor of any power of 10.

Now let us choose any point P on the number axis which does not correspond to a decimal fraction; e.g. the rational point or the irrational point . Then in the process of subdividing the unit interval into ten equal parts, and so on, P will never occur as the initial point of a subinterval. Still, P can be included within smaller and smaller intervals of the decimal division with any desired degree of approximation. This approximation process may be described as follows.

Suppose that P lies in the first unit interval. We subdivide this interval into 10 equal parts, each of length 10^-1, and find, say, that P lies in the third such interval. At this stage we can say that P lies between the decimal fractions 0.2 and 0.3. We subdivide the interval from 0.2 to 0.3 into 10 equal parts, each of length 10^–2, and find that P lies, say, in the fourth such interval. Subdividing this in turn, we find that P lies in the first interval of length 10^-3. We can now say that P lies between 0.230 and 0.231. This process can be continued indefinitely, and leads to an unending sequence of digits, a₁, a₂, a₃, · · ·, a_n, · · ·, with the following property: whatever number n we choose, the point P is included in the interval I_n whose left-hand end-point is the decimal fraction 0. a₁a₂a₃ · · · a_n–1a_n and whose right-hand end-point is 0. a₁a₂a₃ … a_n-1(a_n + 1), the length of I_nbeing 10^–n. If we choose in succession n = 1, 2, 3, 4, · · ·, we see that each of these intervals, I₁, I₂, I₃, · · ·, is contained in the preceding one, while their lengths, 10^–1, 10^–2, 10^–3, · · ·, tend to zero. We say that the point P is contained in a nested sequence of decimal intervals. For example, ifP is the rational point , then all the digits a₁, a₂, a₃, · · · are equal to 3, and P is contained in every interval I_n which extends from 0.333 · · · 33 to 0.333 · · · 34; i.e., 1/3 is greater than 0.333 · · · 33 but less than 0.333 · · · 34, where the number of digits may be taken arbitrarily large. We express this fact by saying that the n-digit decimal fraction 0. 333 · · · 33 “tends to ” as n increases. We write

= 0.333 ··· ,

the dots indicating that the decimal fraction is to be extended “indefinitely.”

The irrational point defined in Article 1 also leads to an indefinitely extended decimal fraction. Here, however, the law which determines the values of the digits in the sequence is by no means obvious. In fact, no explicit formula that determines the successive digits is known, although one may calculate as many digits as desired:

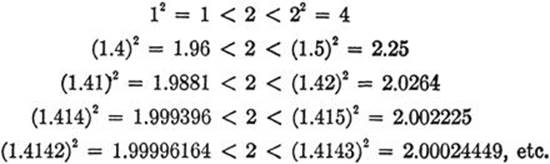
As a general definition we say that a point P that is not represented by any decimal fraction with a finite number n of digits is represented by the infinite decimal fraction, z.a₁a₂a₃ · · ·, if for every value of n the point P lies in the interval of length 10^–n with z.a₁a₂a₃ · · · a_n as its initial point.

In this manner there is established a correspondence between all the points on the number axis and all the finite and infinite decimal fractions We offer the tentative definition: a “number” is a finite or infinite decimal. Those infinite decimals which do not represent rational numbers are called irrational numbers.

Until the middle of the nineteenth century these considerations were accepted as a satisfactory explanation of the system of rational and irrational numbers, the continuum of numbers. The enormous advance of mathematics since the seventeenth century, in particular the development of analytic geometry and of the differential and integral calculus, proceeded safely with this concept of the number system as a basis. But during the period of critical re-examination of principles and consolidation of results, it was felt more and more that the concept of irrational number required a more precise analysis. As a preliminary to our account of the modern theory of the number continuum we shall discuss in a more or less intuitive fashion the basic concept of limit.

Exercise: Calculate and with an accuracy of at least 10^–2.

3. Limits. Infinite Geometrical Series

As we saw in the preceding section, it sometimes happens that a certain rational number s is approximated by a sequence of other rational numbers s_n, where the index n assumes consecutively all the values 1, 2, 3, · · ·. For example, if s = 1/3, then s, = 0.3, s₂ = 0.33, s₃ = 0.333, etc. As another example, let us divide the unit interval into two halves, the second half again into two equal parts, the second of these again into two equal parts, and so forth, until the smallest intervals thus obtained have the length 2^–n, where n is chosen arbitrarily large, e.g. n = 100, n = 100,000, or any number we please. Then by adding together all the intervals except the very last one we obtain a total length equal to

(3) 

We see that s_n differs from 1 by , and that this difference becomes arbitrarily small, or “tends to zero” as n increases indefinitely. It makes no sense to say that the difference is zero if n is infinite. The infinite enters only in the unending procedure and not as an actual quantity. We describe the behavior of s_n by saying that the sum s_n approaches the limit 1 as n tends to infinity, and by writing

(4)  

where on the right we have an infinite series. This “equation” does not mean that we actually have to add infinitely many terms; it is only an abbreviated expression for the fact that 1 is the limit of the finite sum s_n as n tends to infinity (by no means is infinity). Thus equation (4) with its incomplete symbol “+ · · ·” is merely mathematical shorthand for the precise statement

1 = the limit as n tends to infinity of the quantity

(5)  

In an even more abbreviated but expressive form we write

(6)  s_n → 1 as n → ∞.

As another example of limit, we consider the powers of a number q. If – 1 < q < 1, e.g. q = 1/3 or q = –4/5, then the successive powers of q,

q, q², q³, q⁴, · · ·,qⁿ, · · ·,

will approach zero as n increases. If q is negative, the sign of qⁿ will alternate from + to –, and qⁿ will tend to zero from alternate sides Thus if q = 1/3, then q² = 1/9, q³ = 1/27, q⁴ = 1/81, · · ·, while if q = –1/2, then q² = 1/4, q³ = − 1/8, q⁴ = 1/16, · · ·. We say that the limit of qⁿ, as n tends to infinity, is zero, or, in symbols,

(7)  qⁿ → 0 as n → ∞, for – 1 < q < 1.

(Incidentally, if q > 1 or q < –1 then qⁿ does not tend to zero, but increases in magnitude without limit.)

To give a rigorous proof of the assertion (7) we start with the inequality proved on page 15, which states that (1 + p)ⁿ ≥ 1 + np for any positive integer n and p > – 1. If q is any fixed number between 0 and 1, e.g. q = 9/10, we have q = 1/(1 + p), where p > 0. Hence

or (see rule 4, p. 322)

qⁿ is therefore included between the fixed bound 0 and the bound (l/p)(1/n) which approaches zero as n increases, since p is fixed. This makes it evident that qⁿ → 0. If q is negative, we have q = –1/(1 + p) and the bounds become (–1/p)(1/n) and (1/p)(1/n) instead of 0 and (1/p)(1/n). Otherwise the reasoning remains unchanged.

We now consider the geometrical series

(8)   s_n = 1 + q + q² + q³ + · · · + qⁿ.

(The case q = 1/2 was discussed above.) As shown on page 13, we can express the sum s_n in a simple and concise form. If we multiply s_n by q, we find

(8a)   qs_n = q + q² + q³ + q⁴ + · · · + qⁿ⁺¹,

and by subtraction of (8a) from (8) we see that all terms except 1 and qⁿ⁺¹ cancel out. We obtain by this device

(1 – q)s_n = 1 – qⁿ⁺¹,

or, by division,

The concept of limit comes into play if we let n increase. As we have seen, qⁿ⁺¹ = q · qⁿ tends to zero if –1 < q < 1, and we obtain the limiting relation

(9) 

Written as an infinite geometrical series this becomes

(10)

For example,

in agreement with equation (4), and similarly

so that 0.99999 · · · = 1. Similarly, the finite decimal 0.2374 and the infinite decimal 0.23739999999 · · · represent the same number.

In Chapter VI we shall resume the general discussion of the limit concept in the modern spirit of rigor.

Exercises: 1) Prove that

2) What is the limit of the sequence a₁, a₂, a₃, · · ·, where a_n = n/(n + 1)? (Hint: Write the expression in the form n/(n + 1) = 1 – 1/(n + 1) and observe that the second term tends to zero.)

3) What is the limit of (Hint: Write the expression in the form

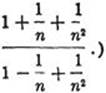
4) Prove, for | q | < 1, that . (Hint: Use the result of exercise 3 on p. 18.)

5) What is the limit of the infinite series

1 – 2q + 3q² – 4q³ + · · · ?

6) What is the limit of , and of ? (Hint: Use the results of pp. 12, 14, 15.)

4. Rational Numbers and Periodic Decimals

Those rational numbers p/q which are not finite decimal fractions can be expanded into infinite decimal fractions by performing the elementary process of long division. At each stage in this process there must be a non-zero remainder, for otherwise the decimal fraction would be finite. All the different remainders that arise in the process of division will be integers between 1 and q–1, so that there are at most q–1 different possibilities for the values of the remainders. This means that within at most q divisions some remainder k will turn up for a second time. But then all subsequent remainders will repeat in the same order in which they appeared after the remainder k first appeared. This shows that the decimal expression for any rational number is periodic; after some finite set of digits has appeared initially, the same digit or group of digits will repeat itself infinitely often. For example, 1/6 = 0.166666666 · · ·; 1/7 = 0.142857142857142857 · · ·; 1/11 = 0.09090909 · · ·; 122/1100 = 0.1109090909 · · ·; 11/90 = 0.122222222...; etc. (Those rational numbers which can be represented as finite decimal fractions may be thought of as having periodic decimal expansions with the figure 0 repeating itself infinitely often after a finite number of digits.) We see, incidentally, that some of these periodic decimals have a non-periodic head before the periodic tail begins.

Conversely, it may be shown that all periodic decimals are rational numbers. As an example, let us take the infinite periodic decimal

p = 0.3322222....

We have p = 33/100 + 10^–32(1 + 10^–1 + 10^–2 +· · ·). The expression in parentheses is the infinite geometrical series

Hence

The proof in the general case is essentially the same, but requires a more general notation. In the general periodic decimal

p = 0.a₁a₂a₃ · · · a_mb₁b₂ · · · a_nb₁b₂ · · · a_nb₁b₂ · · · b_n · · ·

we set 0.b₁b₂ · · · = b_n = B, so that B represents the periodic part of the decimal. Then p becomes

p = 0.a₁a₂ · · · = a_m + 10^–m B(1 + 10^–2n + 10^–3n · · ·).

The expression in parentheses is an infinite geometrical series with q = 10^–n. Its sum, according to equation (10) of the previous article, is 1/(1 – 10^–n), and therefore

Exercises: 1) Expand the fractions into decimal fractions and determine the period.

*2) The number 142,857 has the property that multiplication with any one of the numbers 2, 3, 4, 5, or 6 produces only a cyclic permutation of its digits. Explain this property, using the expansion of ½ into a decimal fraction.

3) Expand the rational numbers of exercise 1 as “decimals” with bases 5, 7. and 12.

4) Expand one-third as a dyadic number.

5) Write. 11212121 · · · as a fraction. Find the value of this symbol if it is meant in the systems with the bases 3 or 5.

5. General Definition of Irrational Numbers by Nested Intervals

On page 63 we adopted the tentative definition: a “number” is a finite or infinite decimal. We agreed that those infinite decimals which do not represent rational numbers should be called irrational numbers. On the basis of the results of the preceding section we may now formulate this definition as follows: the continuum of numbers, or real number system (“real” in contrast to the “imaginary” or “complex” numbers to be introduced in §5) is the totality of infinite decimals. (Finite decimals may be considered as a special case where all digits from a certain point on are zero, or one might just as well prescribe that, instead of taking a finite decimal the last digit of which is a, we write down an infinite decimal with a–1 in place of a, followed by an infinite number of digits all equal to 9. This expresses the fact that .999 · · · = 1, according to Article 3.) The rationalnumbers are the periodic decimals; the irrational numbers are the non-periodic decimals. Even this definition does not seem entirely satisfactory; for, as we have seen in Chapter I, the decimal system is in no way singled out by the nature of things. We might just as well have gone through the reasoning with the dyadic or any other system. For this reason it is desirable to give a more general definition of the number continuum, detached from special reference to the base ten. Perhaps the simplest way to do this is the following:

Let us consider any sequence I₁, I₂, · · ·, I_n, · · · of intervals on the number axis with rational end-points, each of which is contained in the preceding one, and such that the length of the n-th interval I_n tends to zero as n increases. Such a sequence is called a sequence of nested intervals. In the case of decimal intervals the length of I_n is 10^–n but it may just as well be 2^–n or merely restricted to the milder requirement that it be less than 1/n. Now we formulate as a basic postulate of geometry: corresponding to each such sequence of nested intervals there is precisely one point on the number-axis which is contained in all of them. (It is seen directly that there cannot be more than one point common to all the intervals, for the lengths of the intervals tend to zero, and two different points could not both be contained in any interval smaller than the distance between them.) This point is called by definition a real number; if it is not a rational point it is called an irrational number. By this definition we establish a perfect correspondence between points and numbers. It is nothing but a more general formulation of what was expressed by the definition using infinite decimals.

Here the reader may be troubled by an entirely legitimate doubt. What is this “point” on the number axis, which we assumed to belong to all the intervals of a nested sequence, in case it is not a rational point? Our answer is: the existence on the number axis (regarded as a line) of a point contained in every nested sequence of intervals with rational end-points is a fundamental postulate of geometry. No logical reduction of this postulate to other mathematical facts is required. We accept it, just as we accept other axioms or postulates in mathematics, because of its intuitive plausibility and its usefulness in building a consistent system of mathematical thought. From a purely formal point of view, we may start with a line made up only of rational points and then define

Fig. 11. Nested intervals. Limits of sequences.

an irrational point as just a symbol for a certain sequence of nested rational intervals. An irrational point is completely described by a sequence of nested rational intervals with lengths tending to zero. Hence our fundamental postulate really amounts to a definition. To make this definition after having been led to a sequence of nested rational intervals by an intuitive feeling that the irrational point “exists,” is to throw away the intuitive crutch with which our reasoning proceeded and to realize that all the mathematical properties of irrational points may be expressed as properties of nested sequences of rational intervals.

We have here a typical instance of the philosophical position described in the introduction to this book; to discard the naive “realistic” approach that regards a mathematical object as a “thing in itself” of which we humbly investigate the properties, and instead to realize that the only relevant existence of mathematical objects lies in their mathematical properties and in the relations by which they are interconnected. These relations and properties exhaust the possible aspects under which an object can enter the realm of mathematical activity. We give up the mathematical “thing in itself” as physics gave up the unobservable ether. This is the meaning of the “intrinsic” definition of an irrational number as a nested sequence of rational intervals.

The mathematically important point here is that for these irrational numbers, defined as nested sequences of rational intervals, the operations of addition, multiplication, etc., and the relations of “less than” and “greater than,” are capable of immediate generalization from the field of rational numbers in such a way that all the laws which hold in the rational number field are preserved. For example, the addition of two irrational numbers α and β can be defined in terms of the two sequences of nested intervals defining α and β respectively. We construct a third sequence of nested intervals by adding the initial values and the end values of corresponding intervals of the two sequences. The new sequence of nested intervals defines α + β. Similarly, we may define the product αβ, the difference α – β, and the quotient α/β. On the basis of these definitions the arithmetical laws discussed in §1 of this chapter can be shown to hold for irrational numbers also. The details are omitted here.

The verification of these laws is simple and straightforward, though somewhat tedious for the beginner who is more anxious to learn what can be done with mathematics than to analyze its logical foundations. Some modern textbooks on mathematics repel many students by starting with a pedantically complete analysis of the real number system. The reader who simply disregards these introductions may find comfort in the thought that until late in the nineteenth century all the great mathematicians made their discoveries on the basis of the “naive” concept of the number system supplied by their intuition.

From a physical point of view, the definition of an irrational number by a sequence of nested intervals corresponds to the determination of the value of some observable quantity by a sequence of measurements of greater and greater accuracy. Any given operation for determining, say, a length, will have a practical meaning only within the limits of a certain possible error which measures the precision of the operation. Since the rational numbers are dense on the line, it is impossible to determine by any physical operation, however precise, whether a given length is rational or irrational. Thus it might seem that the irrational numbers are unnecessary for the adequate description of physical phenomena. But as we shall see more clearly in Chapter VI, the real advantage which the introduction of irrational numbers brings to the mathematical description of physical phenomena is that this description is enormously simplified by the free use of the limit concept, for which the number continuum is the basis.

*6. Alternative Methods of Defining Irrational Numbers. Dedekind Cuts

A somewhat different way of defining irrational numbers was chosen by Richard Dedekind (1831-1916), one of the great pioneers in the logical and philosophical analysis of the foundations of mathematics. His essays, Stetigkeit und irrationale Zahlen (1872) and Was sind und was sollen die Zahlent? (1887), exercised a profound influence on studies in the foundations of mathematics. Dedekind preferred to operate with general abstract ideas rather than with specific sequences of nested intervals. His procedure is based on the definition of a “cut,” which we shall describe briefly.

Suppose there is given some method for dividing the set of all rational numbers into two classes, A and B, such that every element b of class B is greater than every element a of class A. Any classification of this sort is called a cut in the set of rational numbers. For a cut there are just three possibilities, one and only one of which must hold:

1) There is a largest element a* of A. This is the case, for example, if A consists of all rational numbers ≤ 1 and B of all rational numbers > 1.

2) There is a smallest element b* of B. This is the case, for example, if A consists of all rational numbers < 1 and B of all rational numbers ≥ 1.

3) There is neither a largest element in A nor a smallest element in B. This is the case, for example, if A consists of all negative rational numbers, 0, and all positive rational numbers with square less than 2 and B of all rational numbers with square greater than 2. A and B together include all rational numbers, for we have proved that there is no rational number whose square is equal to 2.

The case in which A has a largest element a* and B a smallest element b* is impossible, for then the rational number (a* + b*)/2, which lies halfway between a* and b*, would be larger than the largest element of A and smaller than the smallest element of B, and hence could belong to neither.

In the third case, where there is neither a largest rational number in A nor a smallest rational number in B, the cut is said by Dedekind to define or simply to be an irrational number. It is easily seen that this definition is in agreement with the definition by nested intervals; any sequence I₁,I₂, I₃, · · · of nested intervals defines a cut if we place in the class A all those rational numbers which are exceeded by the left-hand end-point of at least one of the intervals I_n, and in B all other rational numbers.

Philosophically, Dedekind’s definition of irrational numbers involves a rather high degree of abstraction, since it places no restrictions on the nature of the mathematical law which defines the two classes A and B. A more concrete method of defining the real number continuum is due to Georg Cantor (1845-1918). Although at first sight quite different from the method of nested intervals or of cuts, it is equivalent to either of them, in the sense that the number systems defined in these three ways have the same properties. Cantor’s idea was suggested by the facts that 1) real numbers may be regarded as infinite decimals, and 2) infinite decimals are limits of finite decimal fractions. Freeing ourselves from dependence on the decimal system, we may state with Cantor that any sequence a₁, a₂, a₃, · · · of rational numbers defines a real number if it “converges.” Convergence is understood to mean that the difference (a_m – a_n) between any two members of the sequence tends to zero when a_m and a_n are sufficiently far out in the sequence, i.e. as m and n tend to infinity. (The successive decimal approximations to any number have this property, since any two after the nth can differ by at most 10^–n.) Since there are many ways of approaching the same real number by a sequence of rational numbers, we say that two convergent sequences of rationals a₁, a₂, a₃, · · · and b₁, b₂, b₃, · · · define the same real number if a_n — b_n tends to zero as ηincreases indefinitely. The operations of addition, etc., for such sequences are quite easy to define.