What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

§4. THE MATHEMATICAL ANALYSIS OF INFINITY

1. Fundamental Concepts

The sequence of positive integers

1, 2, 3, · · ·

is the first and most important example of an infinite set. There is no mystery about the fact that this sequence has no end, no “finis”; for, however large be the integer n, the next integer, n + 1, can always be formed. But in the passage from the adjective “infinite,” meaning simply “without end,” to the noun “infinity” we must not make the assumption that “infinity,” usually expressed by the special symbol ∞, can be considered as though it were an ordinary number. We cannot include the symbol ∞ in the real number system and at the same time preserve the fundamental rules of arithmetic. Nevertheless, the concept of the infinite pervades all of mathematics, since mathematical objects are usually studied, not as individuals, but as members of classes or aggregates containing infinitely many objects of the same type, such as the totality of integers, or of real numbers, or of triangles in a plane. For this reason it is necessary to analyze the mathematical infinite in a precise way. The modern theory of sets, created by Georg Cantor and his school at the end of the nineteenth century, has met this challenge with striking success. Cantor’s theory of sets has penetrated and strongly influenced many fields of mathematics, and has become of basic importance in the study of the logical and philosophical foundations of mathematics. The point of departure is the general concept of a set or aggregate. By this is meant any collection of objects defined by some rule which specifies exactly which objects belong to the given collection. As examples we may consider the set of all positive integers, the set of all periodic decimals, the set of all real numbers, or the set of all straight lines in three-dimensional space.

For comparing the “magnitude” of two different sets the basic notion is that of “equivalence.” If the elements in two sets A and B may be paired with each other in such a way that to each element of A there corresponds one and only one element of B and to each element of B corresponds one and only one element of A, then the correspondence is said to be biunique and A and B are said to be equivalent. The notion of equivalence for finite sets coincides with the ordinary notion of equality of number, since two finite sets have the same number of elements if and only if the elements of the two sets can be put into biunique correspondence. This is in fact the very idea of counting, for when we count a finite set of objects, we simply establish a biunique correspondence between these objects and a set of number symbols 1, 2, 3, · · ·, n.

It is not always necessary to count the objects in two finite sets to establish their equivalence. For example, we can assert without counting that any finite set of circles of radius 1 is equivalent to the set of their centers.

Cantor’s idea was to extend the concept of equivalence to infinite sets in order to define an “arithmetic” of infinities. The set of all real numbers and the set of all points on a straight line are equivalent, since the choice of an origin and a unit allows us to associate in a biunique manner with every point P of the line a definite real number x as its coördinate:

P ↔ x.

The even integers form a proper subset of the set of all integers, and the integers form a proper subset of the set of all rational numbers. (By the phrase proper subset of a set S, we mean a set S’ consisting of some, but not all, of the objects in S.) Clearly, if a set is finite, i.e. if it containssome number n of elements and no more, then it cannot be equivalent to any one of its proper subsets, since any proper subset could contain at most n – 1 elements. But, if a set contains infinitely many objects, then, paradoxically enough, it may be equivalent to a proper subset of itself. For example, the coördination

establishes a biunique correspondence between the set of positive integers and the proper subset of even integers, which are thereby shown to be equivalent. This contradiction to the familiar truth, “the whole is greater than any of its parts,” shows what surprises are to be expected in the domain of the infinite.

2. The Denumerability of the Rational Numbers and the Non-Denumerability of the Continuum

One of Cantor’s first discoveries in his analysis of the infinite was that the set of rational numbers (which contains the infinite set of integers as a subset and is therefore itself infinite) is equivalent to the set of integers. At first sight it seems very strange that the dense set of rational numbers should be on the same footing as its sparsely sown subset of integers. True, one cannot arrange the positive rational numbers in order of size (as one can the integers) by saying that a is the first rational number, b the next larger, and so forth, because there are infinitely many rational numbers between any two given ones, and hence there is no “next larger.” But, as Cantor observed, by disregarding the relation of magnitude between successive elements, it is possible to arrange all the rational numbers in a single row, r₁, r₂, r₃, r₄, · · ·, like that of the integers. In this sequence there will be a first rational number, a second, a third, and so forth, and every rational number will appear exactly once. Such an arrangement of a set of objects in a sequence like that of the integers is called. a denumeration of the set. By exhibiting such a denumeration Cantor showed the set of rational numbers to be equivalent with the set of integers, since the correspondence

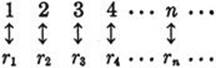
is biunique. One way of denumerating the rational numbers will now be described.

Every rational number can be written in the form a/b, where a and b are integers, and all these numbers can be put in an array, with a/b in the ath column and bth row. For example, 3/4 is found in the third column and fourth row of the table below. All the positive rational numbers may now be arranged according to the following scheme: in the array just defined we draw a continuous, broken line that goes through all the numbers in the array. Starting at 1, we go horizontally to the next place on the right, obtaining 2 as the second member of the sequence, then diagonally down to the left until the first column is reached at the position occupied by 1/2, then vertically down one place to 1/3, diagonally up until the first row is reached again at 3, across to 4, diagonally down to 1/4, and so on, as shown in the figure. Travelling along this broken line we arrive at a sequence 1, 2, 1/2, 1/3, 2/2, 3, 4, 3/2, 2/3, 1/4, 1/5, 2/4, 3/3, 4/2, 5, · · · containing the rational numbers in the order in which they occur along the broken line. In this sequence we now cancel all those numbers a/b for which a and b have a common factor, so that each rational number r will appear exactly once and in its simplest form. Thus we obtain a sequence

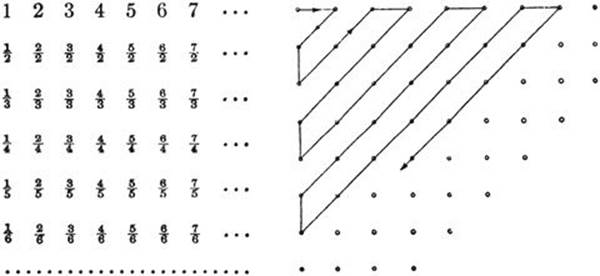
Fig. 19. Denumeration of the rational numbers.

1, 2, 1/2, 1/3, 3, 4, 3/2, 2/3, 1/4, 1/5, 5, · · · which contains each positive rational number once and only once. This shows that the set of all positive rational numbers is denumerable. In view of the fact that the rational numbers correspond in a biunique manner with the rational points on a line, we have proved at the same time that the set of positive rational points on a line is denumerable.

Exercises: 1) Show that the set of all positive and negative integers is denumerable. Show that the set of all positive and negative rational numbers is denumerable.

2) Show that the set S + T (see p. 110) is denumerable if S and T are denumerable sets. Show the same for the sum of three, four, or any number, n, of sets, and finally for a set composed of denumerably many denumerable sets.

Since the rational numbers have been shown to be denumerable, one might suspect that any infinite set is denumerable, and that this is the ultimate result of the analysis of the infinite. This is far from being the case. Cantor made the very significant discovery that the set of all real numbers, rational and irrational, is not denumerable. In other words, the totality of real numbers presents a radically different and, so to speak, higher type of infinity than that of the integers or of the rational numbers alone. Cantor’s ingenious indirect proof of this fact has become a model for many mathematical demonstrations. The outline of the proof is as follows. We start with the tentative assumption that all the real numbers have actually been denumerated in a sequence, and then we exhibit a number which does not occur in the assumed denumeration. This provides a contradiction, since the assumption was that all the real numbers were included in the denumeration, and this assumption must be false if even one number has been left out. Thus the assumption that a denumeration of the real numbers is possible is shown to be untenable, and hence the opposite, i.e. Cantor’s statement that the set of real numbers is not denumerable, is shown to be true.

To carry out this program, let us suppose that we have denumerated all the real numbers by arranging them in a table of infinite decimals,

1st number N₁. a₁a₂a₃a₄a₅ · · ·

2nd number N₂. b₁b₂b₃b₄b₅ · · ·

3rd number N₃. c₁c₂c₃c₄c₅ · ·

where the N’s denote the integral parts and the small letters denote the digits after the decimal point. We assume that this sequence of decimal fractions contains all the real numbers. The essential point in the proof is now to construct by a “diagonal process” a new number which we can show to be not included in this sequence. To do this we first choose a digit a which differs from a₁ and is neither 0 nor 9 (to avoid possible ambiguities which may arise from equalities like 0.999 · · · = 1.000 ’· · ·), then a digit b different from b₂ and again unequal to 0 or 9, similarly cdifferent from c₃, and so on. (For example, we might simply choose a = 1 unless a₁ = 1, in which case we choose a = 2, and similarly down the table for all the digits b, c, d, e, · · · .) Now consider the infinite decimal

z = 0.abcde · · ·.

This new number z is certainly different from any one of the numbers in the table above; it cannot be equal to the first because it differs from it in the first digit after the decimal point; it cannot be equal to the second since it differs from it in the second digit; and, in general, it cannot be identical with the nth number in the table since it differs from it in the nth digit. This shows that our table of consecutively arranged decimals does not contain all the real numbers. Hence this set is not denumerable.

The reader may perhaps imagine that the reason for the nondenumerability of the number continuum lies in the fact that the straight line is infinite in extent, and that a finite segment of the line would contain only a denumerable infinity of points. This is not the case, for it is easy to show that the entire number continuum is equivalent to any finite segment, say the segment from 0 to 1 with the endpoints excluded. The desired biunique correspondence may be obtained by bending the segment at and and projecting from a point, as shown in Figure 20. It follows that even a finite segment of the number axis contains a non-denumerable infinity of points.

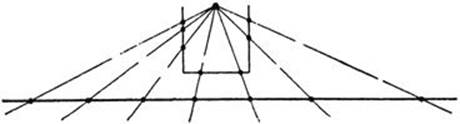
Fig. 20

Fig. 20. Biunique correspondence between the points of a bent segment and a whole straight line.

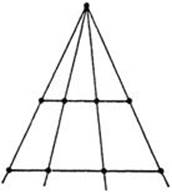
Fig. 21

Fig. 21. Biunique correspondence between the points of two segments of different length.

Exercise: Show that any interval [A, B] of the number axis is equivalent to any other interval [C, D].

It is worthwhile to indicate another and perhaps more intuitive proof of the non-denumerability of the number continuum. In view of what we have just proved it will be sufficient to confine our attention to the set of points between 0 and 1. Again the proof is indirect. Let us suppose that the set of all points on the line between 0 and 1 can be arranged in a sequence

(1) a₁, a₂, a₃, · · ·.

Let us enclose the point with coördinate a₁ in an interval of length 1/10, the point with coordinate a₂ in an interval of length 1/10², and so on. If all points between 0 and 1 were included in the sequence (1), the unit interval would be entirely covered by an infinite sequence of possibly overlapping subintervals of lengths 1/10, 1/10², · · ·. (The fact that some of these extend beyond the unit interval does not influence our proof.) The sum of these lengths is given by the geometric series

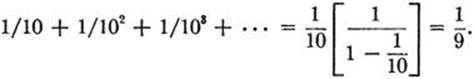
Thus the assumption that the sequence (1) contains all real numbers from 0 to 1 leads to the possibility of covering the whole of an interval of length 1 by a set of intervals of total length 1/9, which is intuitively absurd. We might accept this contradiction as a proof, although from a logical point of view it would require fuller analysis.

The reasoning of the preceding paragraph serves to establish a theorem of great importance in the modern theory of “measure”. Replacing the intervals above by smaller intervals of length ε/10ⁿ, where ε is an arbitrary small positive number, we see that any denumerable set of points on the line can be included in a set of intervals of total length ε/9. Since ε was arbitrary, the latter number can be made as small as we please. In the terminology of measure theory we say that a denumerable set of points has the measure zero.

Exercise: Prove that the same result holds for a denumerable set of points in the plane, replacing lengths of intervals by areas of squares.

3. Cantor’s “Cardinal Numbers”

In summary of the results thus far: The number of elements in a finite set A cannot equal the number of elements in a finite set B if A contains more elements than B. If we replace the concept of “sets with the same (finite) number of elements” by the more general concept of equivalent sets, then with infinite sets the previous statement does not hold; the set of all integers contains more elements than the set of even integers, and the set of rational numbers more than the set of integers, but we have seen that these sets are equivalent. One might suspect that all infinite sets are equivalent and that distinctions other than that between finite numbers and infinity could not be made, but Cantor’s result disproves this; there is a set, the real number continuum, which is not equivalent to any denumerable set.

Thus there are at least two different types of “infinity,” the denumerable infinity of the integers and the non-denumerable infinity of the continuum. If two sets A and B, finite or infinite, are equivalent, we shall say that they have the same cardinal number. This reduces to the ordinary notion of same natural number if A and B are finite, and may be regarded as a valid generalization of this concept. Moreover, if a set A is equivalent with some subset of B, while B is not equivalent to A or to any of its subsets, we shall say, following Cantor, that the set B has a greater cardinal number than the set A. This use of the word “number” also agrees with the ordinary notion of greater number for finite sets. The set of integers is a subset of the set of real numbers, while the set of real numbers is neither equivalent to the set of integers nor to any subset of it (i.e. the set of real numbers is neither denumerable nor finite). Hence, according to our definition, the continuum of real numbers has a greater cardinal number than the set of integers.

* As a matter of fact, Cantor actually showed how to construct a whole sequence of infinite sets with greater and greater cardinal numbers. Since we may start with the set of positive integers, it clearly suffices to show that given any set A it is possible to construct another set B with a greater cardinal number. Because of the great generality of this theorem, the proof is necessarily somewhat abstract. We define the set B to be the set whose elements are all the different subsets of the set A. By the word “subset” we shall include not only the proper subsets of A but also the set A itself, and the empty “subset” 0, containing no elements at all. (Thus, if A consists of the three integers 1, 2, 3, then B contains the 8 different elements {1, 2, 3}, {1, 2}, {1, 3}, {2, 3}, {1}, {2}, {3}, and 0.) Each element of the set B is itself a set, consisting of certain elements of A. Now suppose that B is equivalent to A or to some subset of it, i.e. that there is some rule which correlates in a biunique manner the elements of A or of a subset of A with all the elements of B, i.e. with the subsets of A:

(2)  a ↔ S_a,

where we denote by S_a the subset of A corresponding to the element a of A. We shall arrive at a contradiction by exhibiting an element of B (i.e. a subset T of A) which cannot have any element a correlated with it. In order to construct this subset we observe that for any element x of A two possibilities exist: either the set S_x assigned to x in the given correspondence (2) contains the element x, or S_x does not contain x. We define T as the subset of A consisting of all those elements x such that S_x does not contain x. This subset differs from every S_a by at least the element a, since ifS_a contains a, T does not, while if S_a does not contain a, T does. Hence T is not included in the correspondence (2). This shows that it is impossible to set up a biunique correspondence between the elements of A or of any subset of A and those of B. But the correlation

a ↔ {a}

defines a biunique correspondence between the elements of A and the subset of B consisting of all one-element subsets of A. Hence, by the definition of the last paragraph, B has a greater cardinal number than A.

* Exercise: If A contains n elements, where n is a positive integer, show that B, defined as above, contains 2ⁿ elements. If A consists of the set of all positive integers, show that B is equivalent to the continuum of real numbers from 0 to 1. (Hint: Symbolize a subset of A in the first case by a finite and in the second case by an infinite sequence of the symbols 0 and 1,

a₁a₂a₃ ···,

where a_n = 1 or 0, according as the nth element of A does or does not belong to the given subset.)

One might think it a simple matter to find a set of points with a greater cardinal number than the set of real numbers from 0 to 1. Certainly a square, being “two-dimensional,” would appear to contain “more” points than a “one-dimensional” segment. Surprisingly enough, this is not so; the cardinal number of the set of points in a square is the same as the cardinal number of the set of points on a segment. To prove this we set up the following correspondence.

If (x, y) is a point of the unit square, x and y may be written in decimal form as

x = 0.a₁a₂a₃a₄ ···,

y = 0.b₁b₂b₃b₄ ···,

where to avoid ambiguity we choose, for example, 0.250000 ··· instead of 0.249999 ··· for the rational number ¼. To the point (x, y) of the square we then assign the point

z = 0. a₁b₁a₂b₂a₃b₃a₄b₄···

of the segment from 0 to 1. Clearly, different points (x, y) and (x’, y’) of the square will correspond to different points z and z’ of the segment, so that the cardinal number of the square cannot exceed that of the segment.

(As a matter of fact, the correspondence just defined is biunique between the set of all points of the square and a proper subset of the unit segment; no point of the square could correspond to the point 0.2140909090 ···, for example, since the form 0.25000 ··· rather than 0.24999 ··· was chosen for the number ¼. But it is possible to modify the correspondence slightly so that it will be biunique between the whole square and the whole segment, which are thus seen to have the same cardinal number.)

A similar argument shows that the cardinal number of the points in a cube is no greater than the cardinal number of the segment.

Although these results seem to contradict the intuitive notion of dimensionality, we must remember that the correspondence we have defined is not “continuous”; if we travel along the segment from 0 to 1 continuously, the corresponding points in the square will not form a continuous curve but will appear in a completely chaotic order. The dimension of a set of points depends not only on the cardinal number of the set, but also on the manner in which the points are distributed in space. In Chapter V we shall return to this subject.

4. The Indirect Method of Proof

The theory of cardinal numbers is but one aspect of the general theory of sets, created by Cantor in the face of severe criticism by some of the most distinguished mathematicians of the time. Many of these critics, such as Kronecker and Poincaré, objected to the vagueness of the general concept of “set,” and to the non-constructive character of the reasoning used to define certain sets.

The objections to non-constructive reasoning refer to what may be called essentially indirect proofs. Indirect proofs themselves are a familiar sort of mathematical reasoning: to establish the truth of a statement A, one makes the tentative assumption that A’, the contrary of A, is true. Then by some chain of reasoning one produces a contradiction to A’, thus demonstrating the absurdity of A’. Hence, on the basis of the fundamental logical principle of the “excluded middle,” the absurdity of A’ establishes the truth of A.

Throughout this book we shall meet with examples where an indirect proof can easily be converted into a direct proof, though the indirect form of proof often has the advantages of brevity and freedom from details not necessary for the immediate objective. But there are some theorems for which it has not yet been possible to give other than indirect proofs. There are even theorems, provable by the indirect method, for which direct constructive proofs could not possibly be given even in principle, because of the very nature of the theorems themselves. Such, for example, is the theorem on page 81. On different occasions in the history of mathematics, when the efforts of mathematicians were directed towards constructing solutions for certain problems in order to show their solvability, someone else came along and sidestepped the task of construction by giving an indirect and non-constructive proof.

There is an essential difference between proving the existence of an object of a certain type by constructing a tangible example of such an object, and showing that if none existed one could deduce contradictory results. In the first case one has a tangible object, while in the second case one has only the contradiction. Some distinguished mathematicians have recently advocated the more or less complete banishment from mathematics of all non-constructive proofs. Even if such a program were desirable, it would at present involve tremendous complication and even the partial destruction of the body of living mathematics. For this reason it is no wonder that the school of “intuitionism,” which has adopted this program, has met with strong resistance, and that even the most thoroughgoing intuitionists cannot always live up to their convictions.

5. The Paradoxes of the Infinite

Although the uncompromising position of the intuitionists is far too extreme for most mathematicians, a serious threat to the beautiful theory of infinite aggregates arose when outright logical paradoxes in the theory became apparent. It was soon observed that unrestricted freedom in using the concept of “set” must lead to contradiction. One of the paradoxes, exhibited by Bertrand Russell, may be formulated as follows. Most sets do not contain themselves as elements. For example, the set A of all integers contains as elements only integers; A, being itself not an integer but a set of integers, does not contain itself as element. Such a set we may call “ordinary.” There may possibly be sets which do contain themselves as elements; for example, the set S defined as follows: “S contains as elements all sets definable by an English phrase of less than twenty words” could be considered to contain itself as an element. Such sets we might call “extraordinary” sets. In any case, however, most sets will be ordinary, and we may exclude the erratic behavior of “extraordinary” sets by confining our attention to the set of all ordinary sets. Call this set C. Each element of the set C is itself a set; in fact an ordinary set. The question now arises, is C itself an ordinary set or an extraordinary set? It must be one or the other. If C is ordinary, it contains itself as an element, since C is defined as containing all ordinary sets. This being so, C must be extraordinary, since the extraordinary sets are those containing themselves as members. This is a contradiction. Hence C must be extraordinary. But then C contains as a member an extraordinary set (namely C itself), which contradicts the definition whereby C was to contain ordinary sets only. Thus in either case we see that the assumption of the mere existence of the set C has led us to a contradiction.

6. The Foundations of Mathematics

Paradoxes like this have led Russell and others to a systematic study of the foundations of mathematics and logic. The ultimate aim of their efforts is to provide for mathematical reasoning a logical basis which can be shown to be free from possible contradiction, and which still covers everything that is considered important by all (or some) mathematicians. While this ambitious goal has not been attained and perhaps cannot ever be attained, the subject of mathematical logic has attracted the attention of increasing numbers of students. Many problems in this field which can be stated in very simple terms are very difficult to solve. As an example, we mention the Hypothesis of the Continuum, which states that there is no set whose cardinal number is greater than that of the set of the integers but less than that of the set of real numbers. Many interesting consequences can be deduced from this hypothesis, but up to now it has neither been proved nor disproved, though it has recently been shown by Kurt Gödel that if the usual postulates at the basis of set theory are consistent, then the enlarged set of postulates obtained by adding the Hypothesis of the Continuum is also consistent. Questions such as this ultimately reduce to the question of what is meant by the concept of mathematical existence. Luckily, the existence of mathematics does not depend on a satisfactory answer. The school of “formalists,” led by the great mathematician Hilbert, asserts that in mathematics “existence” simply means “freedom from contradiction.” It then becomes necessary to construct a set of postulates from which all of mathematics can be deduced by purely formal reasoning, and to show that this set of postulates will never lead to a contradiction. Recent results by Gödel and others seem to show that this program, at least as originally conceived by Hilbert, cannot be carried out. Significantly, Hilbert’s theory of the formalized structure of mathematics is essentially based on intuitive procedure. In some way or other, openly or hidden, even under the most uncompromising formalistic, logical, or postulational aspect, constructive intuition always remains the vital element in mathematics.