What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

INTRODUCTION

Construction problems have always been a favorite subject in geometry. With ruler and compass alone a great variety of constructions may be performed, as the reader will remember from school: a line segment or an angle may be bisected, a line may be drawn from a point perpendicular to a given line, a regular hexagon may be inscribed in a circle, etc. In all these problems the ruler is used merely as a straightedge, an instrument for drawing a straight line but not for measuring or marking off distances. The traditional restriction to ruler and compass alone goes back to antiquity, although the Greeks themselves did not hesitate to use other instruments.

One of the most famous of the classical construction problems is the so-called contact problem of Apollonius (circa 200 B.C.) in which three arbitrary circles in the plane are given and a fourth circle tangent to all three is required. In particular, it is permitted that one or more of the given circles have degenerated into a point or a straight line (a “circle” with radius zero or “infinity,” respectively). For example, it may be required to construct a circle tangent to two given straight lines and passing through a given point. While such special cases are rather easily dealt with, the general problem is considerably more difficult.

Of all construction problems, that of constructing with ruler and compass a regular polygon of n sides has perhaps the greatest interest. For certain values of n—e.g. n = 3, 4, 5, 6—the solution has been known since antiquity, and forms an important part of school geometry. But for the regular heptagon (n = 7) the construction has been proved impossible. There are three other classical Greek problems for which a solution has been sought in vain: to trisect an arbitrary given angle, to double a given cube (i.e. to find the edge of a cube whose volume shall be twice that of a cube with a given segment as its edge) and to square the circle (i.e. to construct a square having the same area as a given circle). In all these problems, ruler and compass are the only instruments permitted.

Unsolved problems of this sort gave rise to one of the most remarkable and novel developments in mathematics, when, after centuries of futile search for solutions, the suspicion grew that these problems might be definitely unsolvable. Thus mathematicians were challenged to investigate the question: How is it possible to prove that certain problems cannot be solved?

In algebra, it was the problem of solving equations of degree 5 and higher which led to this new way of thinking. During the sixteenth century mathematicians had learned that algebraic equations of degree 3 or 4 could be solved by a process similar to the elementary method for solving quadratic equations. All these methods have the following characteristic in common: the solutions or “roots” of the equation can be written as algebraic expressions obtained from the coefficients of the equation by a sequence of operations, each of which is either a rational operation—addition, subtraction, multiplication, or division—or the extraction of a square root, cube root, or fourth root. One says that algebraic equations up to the fourth degree can be solved “by radicals” (radix is the Latin word for root). Nothing seemed more natural than to extend this procedure to equations of degree 5 and higher, by using roots of higher order. All such attempts failed. Even distinguished mathematicians of the eighteenth century deceived themselves into thinking that they had found the solution. It was not until early in the nineteenth century that the Italian Ruffini (1765-1822) and the Norwegian genius N. H. Abel (1802-1829) conceived the then revolutionary idea of proving the impossibility of the solution of the general algebraic equation of degree n by means of radicals. One must clearly understand that the question is not whether any algebraic equation of degree n possesses solutions. This fact was first proved by Gauss in his doctoral thesis in 1799. So there is no doubt about the existence of the roots of an equation, especially since these roots can be found by suitable procedures to any degree of accuracy. The art of the numerical solution of equations is, of course, very important and highly developed. But the problem of Abel and Ruffini was quite different: can the solution be effected by means of rational operations and radicals alone? It was the desire to attain full clarity about this question that inspired the magnificent development of modern algebra and group theory started by Ruffini, Abel, and Galois (1811-1832).

The question of proving the impossibility of certain geometrical constructions provides one of the simplest examples of this trend in algebra. By the use of algebraic concepts we shall be able in this chapter to prove the impossibility of trisecting the angle, constructing the regular heptagon, or doubling the cube, by ruler and compass alone. (The problem of squaring the circle is much more difficult to dispose of; see p. 140.) Our point of departure will be not so much the negative question of the impossibility of certain constructions, but rather the positive question: How can all constructible problems be completely characterized? After we have answered this question, it will be an easy matter to show that the problems mentioned above do not fall into this category.

At the age of seventeen Gauss investigated the constructibility of regular “p-gons” (polygons with p sides), where p is a prime number. The construction was then known only for p = 3 and p = 5. Gauss discovered that the regular p-gon is constructible if and only if p is a prime “Fermat number,”

p = 2²ⁿ + 1

The first Fermat numbers are 3, 5, 17, 257, 65537 (see p. 26). So overwhelmed was young Gauss by his discovery that he at once gave up his intention of becoming a philologist and resolved to devote his life to mathematics and its applications. He always looked back on this first of his great feats with particular pride. After his death, a bronze statue of him was erected in Goettingen, and no more fitting honor could be devised than to shape the pedestal in the form of a regular 17-gon.

When dealing with a geometrical construction, one must never forget that the problem is not that of drawing figures in practice with a certain degree of accuracy, but of whether, by the use of straightedge and compass alone, the solution can be found theoretically, supposing our instruments to have perfect precision. What Gauss proved is that his constructions could be performed in principle. His theory does not concern the simplest way actually to perform them or the devices which could be used to simplify and to cut down the number of necessary steps. This is a question of much less theoretical importance. From a practical point of view, no such construction would give as satisfactory a result as could be obtained by the use of a good protractor. Failure properly to understand the theoretical character of the question of geometrical construction and stubbornness in refusing to take cognizance of well-established scientific facts are responsible for the persistence of an unending line of angle-trisectors and circle-squarers. Those among them who are able to understand elementary mathematics might profit by studying this chapter.

Once more it should be emphasized that in some ways our concept of geometrical construction seems artificial. Ruler and compass are certainly the simplest instruments for drawing, but the restriction to these instruments is by no means inherent in geometry. As the Greek mathematicians recognized long ago, certain problems—for example that of doubling the cube—can be solved if, e.g., the use of a ruler in the form of a right angle is permitted; it is just as easy to invent instruments other than the compass by means of which one can draw ellipses, hyperbolas, and more complicated curves, and whose use enlarges considerably the domain of constructible figures. In the next sections, however, we shall adhere to the standard concept of geometrical constructions using only ruler and compass.

PART I. IMPOSSIBILITY PROOFS AND ALGEBRA

§1. FUNDAMENTAL GEOMETRICAL CONSTRUCTIONS

1. Construction of Fields and Square Root Extraction

To shape our general ideas we shall begin by examining a few of the classical constructions. The key to a more profound understanding lies in translating the geometrical problems into the language of algebra. Any geometrical construction problem is of the following type: a certain set of line segments, say a, b, c, · · ·, is given, and one or more other segments x, y, · · ·, are sought. It is always possible to formulate problems in this way, even when at first glance they have a quite different aspect. The required segments may appear as sides of a triangle to be constructed, as radii of circles, or as the rectangular coördinates of certain points (see e.g. p. 137). For simplicity we shall suppose that only one segment x is required. The geometrical construction then amounts to solving an algebraic problem: first we must find a relationship (equation) between the required quantity x and the given quantities a, b, c, · · ·; next we must find the unknown quantity x by solving this equation, and finally we must determine whether this solution can be obtained by algebraic processes that correspond to ruler and compass constructions. It is the principle of analytic geometry, the quantitative characterization of geometrical objects by real numbers, based on the introduction of the real number continuum, that provides the foundation for the whole theory.

First we observe that some of the simplest algebraic operations correspond to elementary geometrical constructions. If two segments are given with lengths a and b (as measured by a given “unit” segment), then it is very easy to construct a + b, a – b, ra (where r is any rational number),a/b, and ab.

To construct a + b (Fig. 27) we draw a straight line and on it mark off with the compass the distances OA = a and AB = b. Then OB = a + b. Similarly, for a – b we mark off OA = a and AB = b, but this time with AB in the opposite direction from OA. Then OB = a – b. To construct 3a we simply add a + a + a; similarly we can construct pa, where p is any integer. We construct a/3 by the following device (Fig. 28): we mark off OA = a on one line, and draw any second line through O. On this line we mark off an arbitrary segment OC = c, and construct OD = 3c. We connect A and D, and draw a line through C parallel to AD, intersecting OA at B. The triangles OBC and OAD are similar; hence OB/a = OB/OA = OC/OD = 1/3, and OB = a/3. In the same way we can construct a/q, where q is any integer. By performing this operation on the segment pa, we can thus construct ra, where r = p/q is any rational number.

Fig. 27. Construction of a + b and a – b.

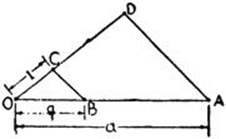
Fig. 28. Construction of a/3.

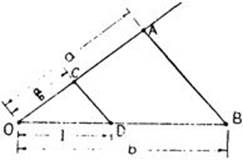
Fig. 29. Construction of a/b.

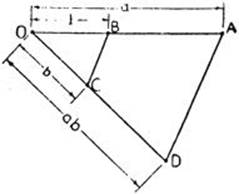
Fig. 30. Construction of ab.

To construct a/b (Fig. 29) we mark off OB = b and OA = a on the sides of any angle O, and on OB we mark off OD = 1. Through D we draw a line parallel to AB meeting OA in C. Then OC will have the length a/b. The construction of ab is shown in Figure 30, where AD is a line parallel to BC through A.

From these considerations it follows that the “rational” algebraic processes, —addition, subtraction, multiplication, and division of known quantities— can be performed by geometrical constructions. From any given segments, measured by real numbers a, b, c,· · ·, we can, by successive application of these simple constructions, construct any quantity that is expressible in terms of a, b, c, · · · in a rational way, i.e. by repeated application of addition, subtraction, multiplication and division. The totality of quantities that can be obtained in this way from a, b, c, · · ·constitute what is called a number field, a set of numbers such that any rational operations applied to two or more members of the set again yield a number of the set. We recall that the rational numbers, the real numbers, and the complex numbers form such fields. In the present case, the field is said to be generated by the given numbers a, b, c, · · ·.

The decisive new construction which carries us beyond the field just obtained is the extraction of a square root: if a segment a is given, then can also be constructed by using only ruler and compass. On a straight line we mark off OA = a and AB = 1 (Fig. 31). We draw a circle with the segment OB as its diameter and construct the perpendicular to OB through A, which meets the circle in C. The triangle OBC has a right angle at C, by the theorem of elementary geometry which states that an angle inscribed in a semicircle is a right angle. Hence, ∠OCA = ∠ABC, the right triangles OAC and CAB are similar, and we have for x = AC,

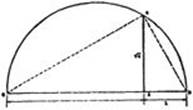
Fig. 31. Construction of .

2. Regular Polygons

Let us now consider a few somewhat more elaborate construction problems. We begin with the regular decagon. Suppose that a regular decagon is inscribed in a circle with radius 1 (Fig. 32), and call its side x. Since x will subtend an angle of 36° at the center of the circle, the other two angles of the large triangle will each be 72°, and hence the dotted line which bisects angle A divides triangle OAB into two isosceles triangles, each with equal sides of length x. The radius of the circle is thus divided into two segments, x and 1 – x. Since OAB is similar to the smaller isosceles triangle, we have 1/x = x/(1 – x). From this proportion we get the quadratic equation x² + x – 1 = 0, the solution of which is . (The other solution of the equation is irrelevant, since it yields a negative x.) From this it is clear that x can be constructed geometrically. Having the length x, we may now construct the regular decagon by marking off this length ten times as a chord of the circle. The regular pentagon may now be constructed by joining alternate vertices of the regular decagon.

Instead of constructing by the method of Figure 31 we can also obtain it as the hypotenuse of a right triangle whose other sides have lengths 1 and 2. We then obtain x by subtracting the unit length from and bisecting the result.

The ratio OB:AB of the preceding problem has been called the golden ratio, because the Greek mathematicians considered a rectangle whose two sides are in this ratio to be aesthetically the most pleasing. Its value, incidentally, is about 1.62.

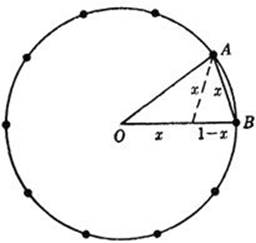
Fig. 32. Regular decagon.

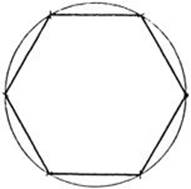
Fig. 33. Regular hexagon.

Of all the regular polygons the hexagon is simplest to construct. We start with a circle of radius r; the length of the side of a regular hexagon inscribed in this circle will then be equal to r. The hexagon itself can be constructed by successively marking off from any point of the circle chords of length r until all six vertices are obtained.

From the regular n-gon we can obtain the regular 2n-gon by bisecting the arc subtended on the circumscribed circle by each edge of the n-gon, using the additional points thus found as well as the original vertices for the required 2n-gon. Starting with the diameter of a circle (a “2-gon”), we can therefore construct the 4, 8, 16, · · ·, 2ⁿ-gon. Similarly, we can obtain the 12-, 24-, 48-gon, etc. from the hexagon, and the 20-, 40-gon, etc. from the decagon.

If s_n denotes the length of the side of the regular n-gon inscribed in the unit circle (circle with radius 1), then the side of the 2n-gon is of length

This may be proved as follows: In Figure 34 s_n is equal to DE = 2DC, s_2n equal to DB, and AB equal to 2. The area of the right triangle ABD is given by ½BD·AD and by . Since , we find, by substituting AB = 2, BD = s_2n, CD = ½s_n, and by equating the two expressions for the area,

Solving this quadratic equation for and observing that x must be less than 2, one easily finds the formula given above.

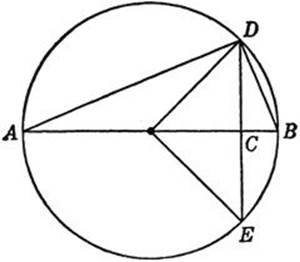
Fig. 34.

From this formula and the fact that s₄ (the side of the square) is equal to it follows that

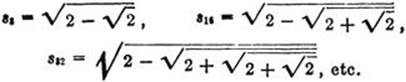
As a general formula we obtain, for n > 2,

with n – 1 nested square roots. The circumference of the 2ⁿ-gon in the circle is 2ⁿ s₂ⁿ. As n tends to infinity, the 2ⁿ-gon tends to the circle. Hence 2ⁿ s₂ⁿ approaches the length of the circumference of the unit circle, which is by definition 2π. Thus we obtain, by substituting m for n – 1 and cancelling a factor 2, the limiting formula for π

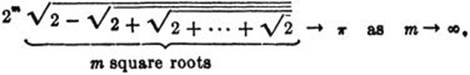
Exercise: Since 2^m→ ∞, prove as a consequence that

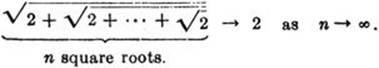
The results obtained thus far exhibit the following characteristic feature: The sides of the 2ⁿ-gon, the 5.2ⁿ-gon, and the 3.2ⁿ-gon, can all be found entirely by the processes of addition, subtraction, multiplication, division, and the extraction of square roots.

*3. Apollonius’ Problem

Another construction problem that becomes quite simple from the algebraic standpoint is the famous contact problem of Apollonius already mentioned. In the present context it is unnecessary for us to find a particularly elegant construction. What matters here is that in principle the problem can be solved by straightedge and compass alone. We shall give a brief indication of the proof, leaving the question of a more elegant method of construction to page 161.

Let the centers of the three given circles have coordinates (x₁, y₁), (x₂, y₂) and (x₃, y₃), respectively, with radii r₁, r₂, and r₃. Denote the center and radius of the required circle by (x, y) and r. Then the condition that the required circle be tangent to the three given circles is obtained by observing that the distance between the centers of two tangent circles is equal to the sum or difference of the radii, according as the circles are tangent externally or internally. This yields the equations

(1) (x – x₁)² + (y – y₁)² – (r ± r₁,)² = 0,

(2) (x – x₂)² + (y – y₂)² – (r ± r₂,)² = 0,

(3) (x – x₃)² + (y – y₃)² – (r ± r₃,)² = 0,

or

(la)

etc. The plus or minus sign is to be chosen in each of these equations according as the circles are to be externally or internally tangent. (See Fig. 35.) Equations (1), (2), (3) are three quadratic equations in three unknowns x, y, r with the property that the second degree terms are the same in each equation, as is seen from the expanded form (1a). Hence, by subtracting (2) from (1), we get a linear equation in x, y, r:

(4) ax + by + cr = d,

where a = 2(x₂ – x₁), etc. Similarly, by subtracting (3) from (1), we get another linear equation,

(5) a’x + b’y + c’r = d’.

Solving (4) and (5) for x and y in terms of r and then substituting in (1) we get a quadratic equation in r, which can be solved by rational operations and the extraction of a square root (see p. 91). There will in general be two solutions of this equation, of which only one will be positive. After finding r from this equation we obtain x and y from the two linear equations (4) and (5). The circle with center (x, y) and radius r will be tangent to the three given circles. In the whole process we have used only rational operations and square root extractions. It follows that r, x, and y can be constructed by ruler and compass alone.

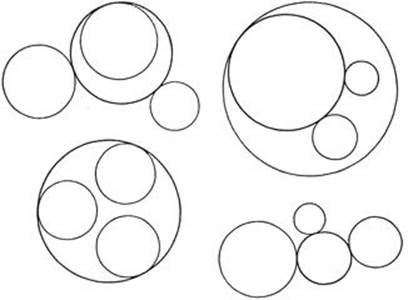
Fig. 35. Apollonius circles.

There will in general be eight solutions of the problem of Apollonius, corresponding to the 2·2·2 = 8 possible combinations of + and – signs in equations (1), (2), and (3). These choices correspond to the conditions that the desired circles be externally or internally tangent to each of the three given circles. It may happen that our algebraic procedure does not actually yield real values for x, y, and r. This will be the case, for example, if the three given circles are concentric, so that no solution to the geometrical problem exists. Likewise, we must expect possible “degenerations” of the solution, as in the case when the three given circles degenerate into three points on a line. Then the Apollonius circle degenerates into this line. We shall not discuss these possibilities in detail; a reader with some algebraic experience will be able to complete the analysis.