What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

§1. INTRODUCTION

1. Classification of Geometrical Properties. Invariance under Transformations

Geometry deals with the properties of figures in the plane or in space. These properties are so numerous and so varied that some principle of classification is necessary to bring order into this wealth of knowledge. One might, for example, introduce a classification based on the method used in deriving the theorems. From this point of view a distinction is usually made between the “synthetic” and the “analytic” procedures. The first of these is the classical axiomatic method of Euclid, in which the subject is built upon purely geometrical foundations independent of algebra and the concept of the number continuum, and in which the theorems are deduced by logical reasoning from an initial body of statements called axioms or postulates. The second method is based on the introduction of numerical coördinates, and uses the technique of algebra. This method has brought about a profound change in mathematical science, resulting in a unification of geometry, analysis and algebra into one organic system.

In this chapter a classification according to method will be less important than a classification according to content, based on the character of the theorems themselves, irrespective of the methods used to prove them. In elementary plane geometry one distinguishes between theorems dealing with the congruence of figures, using the concepts of length and angle, and theorems dealing with the similarity of figures, using the concept of angle only. This particular distinction is not very important, since length and angle are so closely connected that it is rather artificial to separate them. (It is the study of this connection which makes up most of the subject of trigonometry.) Instead, we may say that the theorems of elementary geometry concern magnitudes—lengths, measures of angles, and areas. Two figures are equivalent from this point of view if they arecongruent, that is, if one can be obtained from the other by a rigid motion, in which merely position but no magnitude is changed. The question now arises whether the concept of magnitude and the related concepts of congruence and similarity are essential to geometry, or whether geometrical figures may have even deeper properties that are not destroyed by transformations more drastic than the rigid motions. We shall see that this is indeed the case.

Suppose we draw a circle and a pair of its perpendicular diameters on a rectangular block of soft wood, as in Figure 69. If we place this block between the jaws of a powerful vise and compress it to half its original width, the circle will become an ellipse and the angles between the diameters of the ellipse will no longer be right angles. The circle has the property that its points are equidistant from the center, while this does not hold true of the ellipse. Thus it might seem that all the geometrical properties of the original configuration are destroyed by the compression. But this is far from being the case; for example, the statement that the center bisects each diameter is true of both the circle and the ellipse. Here we have a property which persists even after a rather drastic change in the magnitudes of the original figure. This observation suggests the possibility of classifying theorems about a geometrical figure according to whether they remain true or become false when the figure is subjected to a uniform compression. More generally, given any definite class of transformations of a figure (such as the class of all rigid motions, compressions, inversion in circles, etc.), we may ask what properties of the figure will be unchanged under this class of transformations. The body of theorems dealing with these properties will be the geometry associated with this class of transformations. The idea of classifying the different branches of geometry according to the classes of transformations considered was proposed by Felix Klein (1849–1925) in a famous address (the “Erlanger program”) given in 1872. Since that time it has greatly influenced geometrical thinking.

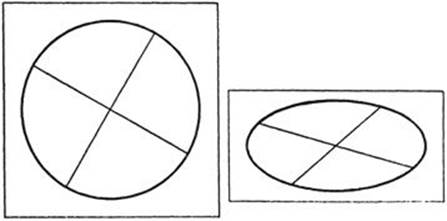
Fig. 69. Compression of a circle.

In Chapter V we shall discover the very surprising fact that certain properties of geometrical figures are so deeply inherent that they persist even after the figures are subjected to quite arbitrary deformations; figures drawn on a piece of rubber which is stretched or compressed in any manner still preserve some of their original characteristics. In this chapter, however, we shall be concerned with those properties which remain unchanged, or “invariant,” under a special class of transformations which lies between the very restricted class of rigid motions on the one hand, and the most general class of arbitrary deformations on the other. This is the class of “projective transformations.”

2. Projective Transformations

The study of these geometrical properties was forced upon mathematicians long ago by the problems of perspective, which were studied by artists such as Leonardo da Vinci and Albrecht Dürer. The image made by a painter can be regarded as a projection of the original onto the canvas, with the center of projection at the eye of the painter. In this process lengths and angles are necessarily distorted, in a way that depends on the relative positions of the various objects depicted. Still, the geometrical structure of the original can usually be recognized on the canvas. How is this possible? It must be because there exist geometrical properties “invariant under projection”—properties which appear unchanged in the image and make the identification possible. To find and analyze these properties is the object of projective geometry.

It is clear that the theorems in this branch of geometry cannot be statements about lengths and angles or about congruence. Some isolated facts of a projective nature have been known since the seventeenth century and even, as in the case of the “theorem of Menelaus,” since antiquity. But a systematic study of projective geometry was first made at the end of the eighteenth century, when the Ecole Polytechnique in Paris initiated a new period in mathematical progress, particularly in geometry. This school, a product of the French Revolution, produced many officers for the military services of the Republic. One of its graduates was J. V. Poncelet (1788–1867), who wrote his famous Traité des propriétés projectives des figures in 1813, while a prisoner of war in Russia. In the nineteenth century, under the influence of Steiner, von Staudt, Chasles, and others, projective geometry became one of the chief subjects of mathematical research. Its popularity was due partly to its great aesthetic charm and partly to its clarifying effect on geometry as a whole and its intimate connection with non-Euclidean geometry and algebra.