What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

§9. AXIOMATICS AND NON-EUCLIDEAN GEOMETRY

1. The Axiomatic Method

The axiomatic method in mathematics goes back at least as far as Euclid. By no means is it true that Greek mathematics was developed or presented exclusively in the rigid postulational form of the Elements. But so great was the impression made by this work on subsequent generations that it became a model for all rigorous demonstration in mathematics. Sometimes even philosophers, e.g. Spinoza in his Ethica, more geometrico demonstrata, tried to present arguments in the form of theorems deduced from definitions and axioms. In modern mathematics, after a departure from the Euclidean tradition during the seventeenth and eighteenth centuries, there has been an increasing penetration of the axiomatic method into every field. One of the most recent results has been the creation of a new discipline, mathematical logic.

In general terms the axiomatic point of view can be described as follows: To prove a theorem in a deductive system is to show that the theorem is a necessary logical consequence of some previously proved propositions; these, in, turn, must themselves be proved; and so on. The process of mathematical proof would therefore be the impossible task of an infinite regression unless, in going back, one is permitted to stop at some point. Hence there must be a number of statements, called postulates or axioms, which are accepted as true, and for which proof is not required. From these we may attempt to deduce all other theorems by purely logical argument. If the facts of a scientific field are brought into such a logical order that all can be shown to follow from a selected number of (preferably few, simple, and plausible) statements, then the field is said to be presented in an axiomatic form. The choice of the propositions selected as axioms is to a large extent arbitrary. But little is gained by the axiomatic method unless the postulates are simple and not too great in number. Moreover, the postulates must be consistent, in the sense that no two theorems deducible from them can be mutually contradictory, and complete, so that every theorem of the system is deducible from them. For reasons of economy it is also desirable that the postulates be independent, in the sense that no one of them is a logical consequence of the others. The question of the consistency and of the completeness of a set of axioms has been the subject of much controversy. Different philosophical convictions concerning the ultimate roots of human knowledge have led to apparently irreconcilable views on the foundations of mathematics. If mathematical entities are considered as substantial objects in a realm of “pure intuition”, independent of definitions and of individual acts of the human mind, then of course there can be no contradictions, since mathematical facts are objectively true statements describing existing realities. From this “Kantian” point of view there is no problem of consistency. Unfortunately, however, the actual body of mathematics cannot be fitted into such a simple philosophical framework. The modern mathematical intuitionists do not rely on pure intuition in the broad Kantian sense. They accept the denumerably infinite as the legitimate child of intuition, and they admit only constructive properties; but thus basic concepts such as the number continuum would be banished, important parts of actual mathematics excluded, and the rest almost hopelessly complicated.

Quite different is the view taken by the “formalists.” They do not attribute an intuitive reality to mathematical objects, nor do they claim that axioms express obvious truths concerning the realities of pure intuition; their concern is only with the formal logical procedure of reasoning on the basis of postulates. This attitude has a definite advantage over intuitionism, since it grants to mathematics all the freedom necessary for theory and applications. But it imposes on the formalist the necessity of proving that his axioms, now appearing as arbitrary creations of the human mind, cannot possibly lead to a contradiction. Great efforts have been made during the last twenty years to find such consistency proofs, at least for the axioms of arithmetic and algebra and for the concept of the number continuum. The results are highly significant, but success is still far off. Indeed, recent results indicate that such efforts cannot be completely successful, in the sense that proofs for consistency and completeness are not possible within strictly closed systems of concepts. Remarkably enough, all these arguments on foundations proceed by methods that in themselves are thoroughly constructive and directed by intuitive patterns.

Accentuated by the paradoxes of set theory (see p. 87), the clash between the intuitionists and the formalists has been much publicized by passionate partisans of these schools. The mathematical world has resounded with a cry about the “crisis in the foundations.” But the alarm was not, and must not be, taken too seriously. With all credit to the achievements produced in the struggle for clarification of the foundations, it would be completely unjustified to infer that the living body of mathematics is in the least threatened by such differences of opinion or by the paradoxes inherent in an uncontrolled drift towards boundless generality.

Quite apart from philosophical considerations and from interest in foundations, the axiomatic approach to a mathematical subject is the natural way to unravel the network of interconnections between the various facts and to exhibit the essential logical skeleton of the structure. It sometimes happens that such a concentration on the formal structure rather than on the intuitive meaning of the concepts makes it easier to find generalizations and applications that might have been overlooked in a more intuitive approach. But a significant discovery or an illuminating insight is rarely obtained by an exclusively axiomatic procedure. Constructive thinking, guided by the intuition, is the true source of mathematical dynamics. Although the axiomatic form is an ideal, it is a dangerous fallacy to believe that axiomatics constitutes the essence of mathematics. The constructive intuition of the mathematician brings to mathematics a non-deductive and irrational element which makes it comparable to music and art.

Since the days of Euclid, geometry has been the prototype of an axiomatized discipline. For centuries Euclid’s set of axioms has been the object of intensive study. But only recently has it become apparent that his postulates must be modified and completed if all of elementary geometry is to be deducible from them. Late in the nineteenth century, for example, Pasch discovered that the ordering of points on a line, the notion of “betweenness,” requires a special postulate. Pasch formulated the following statement as an axiom: A straight line that intersects one side of a triangle in any point other than a vertex must also intersect another side of the triangle. (Lack of regard for such details leads to many apparent paradoxes in which absurd consequences—e.g. the well-known “proof” that every triangle is isosceles—seem to be deduced rigorously from Euclid’s axioms. This is usually done on the basis of an improperly drawn figure whose lines seem to intersect inside or outside certain triangles or circles, whereas they really do not.)

In his famous book, Grundlagen der Geometrie (first edition published in 1901), Hilbert gave a satisfactory set of axioms for geometry and at the same time made an exhaustive study of their mutual independence, consistency, and completeness.

Into any set of axioms there must enter certain undefined concepts, such as “point” and “line” in geometry. Their “meaning” or connection with objects of the physical world is mathematically unessential. They can be regarded as purely abstract entities whose mathematical properties in a deductive system are given entirely by the relations that hold among them as stated by the axioms. For example, in projective geometry we might begin with the undefined concepts of “point,” “line,” and “incidence,” and with the two dual axioms: “Each two distinct points are incident with a unique line” and “Each two distinct lines are incident with a unique point.” From the point of view of axiomatics, the dual form of such axioms is the very source of the principle of duality in projective geometry. Any theorem which contains in its statement and proof only elements connected by dual axioms must admit of dualization. For the proof of the original theorem consists in the successive application of certain axioms, and the application of the dual axioms in the same order will provide a proof for the dual theorem.

The totality of axioms of geometry provides the implicit definition of all “undefined” geometrical terms such as “line,” “point,” “incident,” etc. For applications it is important that the concepts and axioms of geometry correspond well with physically verifiable statements about “real,” tangible objects. The physical reality behind the concept of “point” is that of a very small object, such as a pencil dot, while a “straight line” is an abstraction from a stretched thread or a ray of light. The properties of these physical points and straight lines are found by experience to agree more or less with the formal axioms of geometry. Quite conceivably more precise experiments might necessitate modification of these axioms if they are adequately to describe physical phenomena. But if the formal axioms did not agree more or less with the properties of physical objects, then geometry would be of little interest. Thus, even for the formalist, there is an authority other than the human mind, that decides the direction of mathematical thought.

2. Hyperbolic Non-Euclidean Geometry

There is one axiom of Euclidean geometry whose “truth,” that is, whose correspondence with empirical data about stretched threads or light rays, is by no means obvious. This is the famous postulate of the unique parallel, which states that through any point not on a given line one and only one line can be drawn parallel to the given line. The remarkable feature of this axiom is that it makes an assertion about the whole extent of a straight line, imagined as extending indefinitely in either direction; for to say that two lines are parallel is to say that they never intersect, no matter how far they may be produced. It goes without saying that there are many lines through a point which do not intersect a given line within any fixed finite distance, however large. Since the maximum possible length of an actual ruler, thread, or even a light ray visible to a telescope is certainly finite, and since within any finite circle there are infinitely many straight lines through a given point and not intersecting a given line inside the circle, it follows that this axiom can never be verified by experiment. All the other axioms of Euclidean geometry have a finite character in that they deal with finite portions of lines and with plane figures of finite extent. The fact that the parallel axiom is not experimentally verifiable raises the question of whether or not it is independent of the other axioms. If it were a necessary logical consequence of the others, then it would be possible to strike it out as an axiom and to give a proof of it in terms of the other Euclidean axioms. For centuries mathematicians tried to find such a proof, because of the widespread feeling among students of geometry that the parallel postulate is of a character essentially different from the others, lacking the sort of compelling plausibility which an axiom of geometry should possess. One of the first attempts of this nature was made by Proclus (fourth century A.D.), a commentator on Euclid, who tried to dispense with the need for a special parallel postulate by defining the parallel to a given line to be the locus of all points at a given fixed distance from the line. In this he failed to observe that the difficulty was only shifted to another place, for it would then be necessary to prove that the locus of such points is in fact a straight line. Since Proclus could not prove this, he would have to accept it instead of the parallel axiom as a postulate, and nothing would be gained, for the two are easily seen to be equivalent. The Jesuit Saccheri (1667–1733), and later Lambert (1728–1777), tried to prove the parallel postulate by the indirect method of assuming the contrary and drawing absurd consequences. Far from being absurd, their conclusions really amounted to theorems of the non-Euclidean geometry developed later. Had they regarded them not as absurdities, but rather as self-consistent statements, they would have been the discoverers of non-Euclidean geometry.

At that time, any geometrical system not absolutely in accordance with Euclid’s would have been considered as obvious nonsense. Kant, the most influential philosopher of the period, formulated this attitude in the statement that Euclid’s axioms are inherent in the human mind, and therefore have an objective validity for “real” space. This belief in the axioms of Euclidean geometry as unalterable truths, existing in the realm of pure intuition, was one of the basic tenets of Kant’s philosophy. But in the long run, neither old habits of thinking nor philosophical authority could suppress the conviction that the unending record of failure in the search for a proof of the parallel postulate was due not to any lack of ingenuity, but rather to the fact that the parallel postulate is really independent of the others. (In much the same way, the lack of success in proving that the general equation of the fifth degree could be solved by radicals led to the suspicion, later verified, that such a solution is impossible.) The Hungarian Bolyai (1802–1860) and the Russian Lobachevsky (1793–1856), settled the question by constructing in all detail a geometry in which the parallel axiom does not hold. When the enthusiastic young genius Bolyai submitted his paper to Gauss, the “prince of mathematicians,” for the recognition he so eagerly expected, he was informed that his work had been anticipated by Gauss himself, but that the latter had not cared to publish his results because he dreaded noisy publicity.

What does the independence of the parallel postulate mean? Simply that it is possible to construct a consistent system of “geometrical” statements dealing with points, lines, etc., by deduction from a set of axioms in which the parallel postulate is replaced by a contrary postulate. Such a system is called a non-Euclidean geometry. It required the intellectual courage of Gauss, Bolyai, and Lobachevsky to realize that such a geometry, based on a non-Euclidean system of axioms, can be perfectly consistent.

To show the consistency of the new geometry, it is not enough to deduce a large body of non-Euclidean theorems, as Bolyai and Lobachevsky did. Instead, we have learned to build “models” of such a geometry which satisfy all the axioms of Euclid except for the parallel postulate. The simplest such model was given by Felix Klein, whose work in the field was stimulated by the ideas of the English geometer Cayley (1821–1895). In this model, infinitely many “straight lines” can be drawn “parallel” to a given line through an external point. Such a geometry is called Bolyai-Lobachevskian or “hyperbolic” geometry. (The reason for the latter name will be found on p. 226.)

Klein’s model is constructed by first considering objects of ordinary Euclidean geometry and then renaming certain of these objects and the relations between them in such a way that a non-Euclidean geometry arises. This must, eo ipso, be just as consistent as the original Euclidean geometry, because it is presented to us, seen from another point of view and described with other words, as a body of facts of ordinary Euclidean geometry. This model can be easily understood by means of some concepts of projective geometry.

If we subject the plane to a projective transformation onto another plane, or rather onto itself (by afterwards making the image plane coincide with the original plane), then, in general, a circle and its interior will be transformed into a conic section. But one can easily show (the proof is omitted here) that there exist infinitely many projective transformations of the plane onto itself such that a given circle plus its interior is transformed into itself. By such transformations points of the interior or of the boundary are in general shifted to other positions, but remain inside or on the boundary of the circle. (As a matter of fact, one can move the center of the circle into any other interior point.) Let us consider the totality of such transformations. Certainly they will not leave the shapes of figures invariant, and are therefore not rigid displacements in the usual sense. But now we take the decisive step of calling them “non-Euclidean displacements” in the geometry to be constructed. By means of these “displacements” we are able to define congruence—two figures being called congruent if there exists a non-Euclidean displacement transforming one into the other.

The Klein model of hyperbolic geometry is then the following: The “plane” consists only of the points interior to the circle; points outside are disregarded. Each point inside the circle is called a non-Euclidean “point”; each chord of the circle is called a non-Euclidean “straight line”; “displacement” and “congruence” are defined as above; joining “points” and finding the intersection of “straight lines” in the non-Euclidean sense remain the same as in Euclidean geometry. It is an easy matter to show that the new system satisfies all the postulates of Euclidean geometry, with the one exception of the parallel postulate. That the parallel postulate does not hold in the new system is shown by the fact that through any “point” not on a “straight line” infinitely many “straight lines” can be drawn having no “point” in common with the given “line.” The first “straight line” is a Euclidean chord of the circle, while the second “straight line” may be any one of the chords which pass through the given “point” and do not intersect the first “line” inside the circle. This simple model is quite sufficient to settle the fundamental question which gave rise to non-Euclidean geometry; it proves that the parallel postulate cannot be deduced from the other axioms of Euclidean geometry. For if it could be so deduced, it would be a true theorem in the geometry of Klein’s model, and we have seen that it is not.

Strictly speaking, this argument is based on the assumption that the geometry of Klein’s model is consistent, so that a theorem together with its contrary cannot be proved. But the geometry of Klein’s model is certainly as consistent as ordinary Euclidean geometry, since statements concerning “points,” “lines,” etc. in Klein’s model are merely different ways of phrasing certain theorems of Euclidean geometry. A satisfactory proof of the consistency of the axioms of Euclidean geometry has never been given, except by referring back to the concepts of analytic geometry and hence ultimately to the number continuum, whose consistency is again an open question.

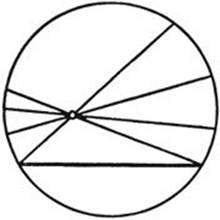
Fig. 110. Klein’s non-Euclidean model.

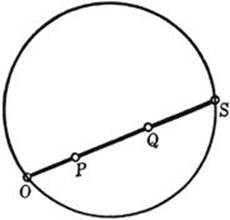
Fig. 111. Non-Euclidean distance.

* One detail which goes beyond the immediate objective should be mentioned here, namely, how to define non-Euclidean “distance” in Klein’s model. This “distance” is required to be invariant under any non-Euclidean “displacement”; for displacement should leave distances invariant. We know that cross-ratios are invariant under projection. A cross-ratio involving two arbitrary points P and Q inside the circle presents itself immediately if the segment PQ is extended to meet the circle in O and S. The cross-ratio (OSQP) of these four points is a (positive) number, which one might hope to take as the definition of the “distance” PQ between P and Q. But this definition must be modified slightly to make it workable. For if the three points P, Q, R are on a line, it should be true that . Now in general

(OSQP) + (OSRQ) ≠ (OSRP).

Instead, we have the relation

(1) (OSQP)(OSRQ) = (OSRP),

as is seen from the equations

In consequence of the equation (1) we can give a satisfactory additive definition by measuring “distance,” not by the cross-ratio itself, but by the logarithm of the cross-ratio:

= non-Euclidean distance from P to Q = log (OSQP).

This distance will be a positive number, since (OSQP) > 1 if P ≠ Q. Using the fundamental property of the logarithm (see p. 444), it follows from (1) that . The base chosen for the logarithm is of no importance, since change of base merely changes the unit of measurement. Incidentally, if one of the points, e.g. Q, approaches the circle, then the non-Euclidean distance will increase to infinity. This shows that the straight line of our non-Euclidean geometry is of infinite non-Euclidean length, although in the ordinary Euclidean sense it is only a finite segment of a straight line.

3. Geometry and Reality

The Klein model shows that hyperbolic geometry, viewed as a formal deductive system, is as consistent as the classical Euclidean geometry. The question then arises, which of the two is to be preferred as a description of the geometry of the physical world? As we have already seen, experiment can never decide whether there is but one or whether there are infinitely many straight lines through a point and parallel to a given line. In Euclidean geometry, however, the sum of the angles of any triangle is 180°, while it can be shown that in hyperbolic geometry the sum is less than 180°. Gauss accordingly performed an experiment to settle the question. He accurately measured the angles in a triangle formed by three fairly distant mountain peaks, and found the angle-sum to be 180°, within the limits of experimental error. Had the result been noticeably less than 180°, the consequence would have been that hyperbolic geometry is preferable to describe physical reality. But, as it turned out, nothing was settled by this experiment, since for small triangles whose sides are only a few miles in length the deviation from 180° in the hyperbolic geometry might be so small as to have been undetectable by Gauss’s instruments. Thus, although the experiment was inconclusive, it showed that the Euclidean and hyperbolic geometries, which differ widely in the large, coincide so closely for relatively small figures that they are experimentally equivalent. Therefore, as long as purely local properties of space are under consideration, the choice between the two geometries is to be made solely on the basis of simplicity and convenience. Since the Euclidean system is rather simpler to deal with, we are justified in using it exclusively, as long as fairly small distances (of a few million miles!) are under consideration. But we should not necessarily expect it to be suitable for describing the universe as a whole, in its largest aspects. The situation here is precisely analogous to that which exists in physics, where the systems of Newton and Einstein give the same results for small distances and velocities, but diverge when very large magnitudes are involved.

The revolutionary importance of the discovery of non-Euclidean geometry lay in the fact that it demolished the notion of the axioms of Euclid as the immutable mathematical framework into which our experimental knowledge of physical reality must be fitted.

4. Poincaré’s Model

The mathematician is free to consider a “geometry” as defined by any set of consistent axioms about “points,” “straight lines,” etc.; his investigations will be useful to the physicist only if these axioms correspond to the physical behavior of objects in the real world. From this point of view we wish to examine the meaning of the statement “light travels in a straight line.” If this is regarded as the physical definition of “straight line,” then the axioms of geometry must be so chosen as to correspond with the behavior of light rays. Let us imagine, with Poincaré, a world composed of the interior of a circle C, and such that the velocity of light at any point inside the circle is equal to the distance of that point from the circumference. It can be proved that rays of light will then take the form of circular arcs perpendicular at their extremities to the circumferenceC. In such a world, the geometrical properties of “straight lines” (defined as light rays) will differ from the Euclidean properties of straight lines. In particular, the parallel axiom will not hold, since there will be infinitely many “straight lines” through any point which do not intersect a given “straight line.” As a matter of fact, the “points” and “straight lines” in this world will have exactly the geometrical properties of the “points” and “lines” of the Klein model. In other words, we shall have a different model of a hyperbolic geometry. But Euclidean geometry will also apply in this world; instead of being non-Euclidean “straight lines,” the light rays would be Euclidean circles perpendicular to C. Thus we see that different systems of geometry can describe the same physical situation, provided that the physical objects (in this case, light rays) are correlated with different concepts of the two systems:

light ray → “straight line”—hyperbolic geometry

light ray → “circle”—Euclidean geometry.

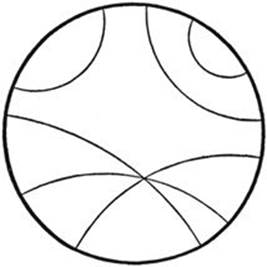
Fig. 112. Poincaré’s non-Euclidean model.

Since the concept of a straight line in Euclidean geometry corresponds to the behavior of a light ray in a homogeneous medium, we would say that the geometry of the region inside C is hyperbolic, meaning only that the physical properties of light rays in this world correspond to the properties of the “straight lines” of hyperbolic geometry.

5. Elliptic or Riemannian Geometry

In Euclidean geometry, as well as in the hyperbolic or Bolyai-Lobachevskian geometry, the tacit assumption is made that the line is infinite (the infinite extent of the line is essentially tied up with the concept and the axioms of “betweenness”). But after hyperbolic geometry had opened the way for freedom in constructing geometries, it was only natural to ask whether different non-Euclidean geometries could be constructed in which a straight line is not infinite but finite and closed. Of course, in such geometries not only the parallel postulate, but also the axioms of “betweenness” will have to be abandoned. Modern developments have brought out the physical importance of these geometries. They were first considered in the inaugural address delivered in 1851 by Riemann upon his admission as an unpaid instructor (“Privat-Docent”) at the University of Goettingen. Geometries with closed finite lines can be constructed in a completely consistent way. Let us imagine a two-dimensional world consisting of the surface S of a sphere, in which we define “straight line” to mean great circle of the sphere. This would be the natural way to describe the world of a navigator, since the arcs of great circles are the curves of shortest length between two points on a sphere and this is a characteristic property of straight lines in the plane. In such a world, every two “straight lines” intersect, so that from an external point no line can be drawn parallel to (i.e. not intersecting) a given “straight line.” The geometry of “straight lines” in this world is called an elliptic geometry. In this geometry, the distance between two points is measured simply by the distance along the shorter arc of the great circle connecting the points. Angles are measured as in Euclidean geometry. We generally consider as typical of an elliptic geometry the fact that no parallel exists to a line.

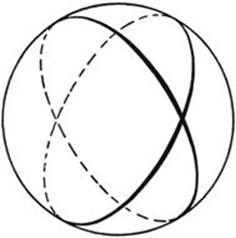
Fig. 113. “Straight lines” in a Riemannian geometry.

Following Riemann, we can generalize this geometry as follows. Let us consider a world consisting of a curved surface in space, not necessarily a sphere, and let us define the “straight line” joining any two points to be the curve of shortest length or “geodesic” joining these points. The points of the surface can be divided into two classes:—1. Points in the neighborhood of which the surface is like a sphere in that it lies wholly on one side of the tangent plane at the point. 2. Points in the neighborhood of which the surface is saddle-shaped, and lies on both sides of the tangent plane at the point. Points of the first kind are called elliptic points of the surface, since, if the tangent plane is shifted slightly parallel to itself, it intersects the surface in an elliptical curve; while points of the second kind are called hyperbolic, since, if the tangent plane is shifted slightly parallel to itself, it intersects the surface in a curve resembling a hyperbola. The geometry of the geodesic “straight lines” in the neighborhood of a point of the surface is elliptic or hyperbolic according as the point is an elliptic or hyperbolic point. In such a model of non-Euclidean geometry, angles are measured by their ordinary Euclidean value.

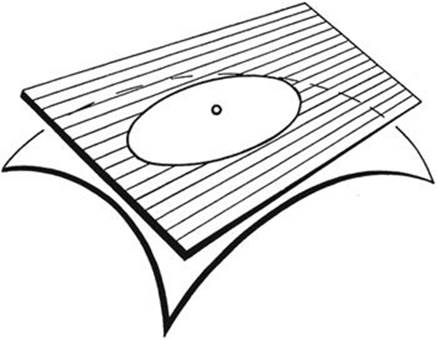
Fig. 114. Elliptic point.

This idea was developed by Riemann, who considered a geometry of space analogous to this geometry of a surface, in which the “curvature” of space may change the character of the geometry from point to point. The “straight lines” in a Riemannian geometry are the geodesics. In Einstein’s general theory of relativity the geometry of space is a Riemannian geometry, light travels along geodesics, and the curvature of space is determined by the nature of the matter that fills it.

From its origin in the study of axiomatics, non-Euclidean geometry has developed into an exceedingly useful instrument for application to the physical world. In the theory of relativity, in optics, and in the general theory of wave propagation, a non-Euclidean description of phenomena is sometimes far more adequate than a Euclidean one.

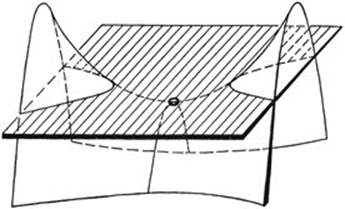
Fig. 115. Hyperbolio point.