What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

§2. TOPOLOGICAL PROPERTIES OF FIGURES

1. Topological Properties

We have proved that the Euler formula holds for any simple polyhedron. But the range of validity of this formula goes far beyond the polyhedra of elementary geometry, with their flat faces and straight edges; the proof just given would apply equally well to a simple polyhedron with curved faces and edges, or to any subdivision of the surface of a sphere into regions bounded by curved arcs. Moreover, if we imagine the surface of the polyhedron or of the sphere to be made out of a thin sheet of rubber, the Euler formula will still hold if the surface is deformed by bending and stretching the rubber into any other shape, so long as the rubber is not torn in the process. For the formula is concerned only with the numbers of the vertices, edges, and faces, and not with lengths, areas, straightness, cross-ratios, or any of the usual concepts of elementary or projective geometry.

We recall that elementary geometry deals with the magnitudes (length, angle, and area) that are unchanged by the rigid motions, while projective geometry deals with the concepts (point, line, incidence, and cross-ratio) which are unchanged by the still larger group of projective transformations. But the rigid motions and the projections are both very special cases of what are called topological transformations: a topological transformation of one geometrical figure A into another figure A’ is given by any correspondence

p ↔ p’

between the points p of A and the points p’ of A’ which has the following two properties:

1. The correspondence is biunique. This means that to each point p of A corresponds just one point p’ of A’, and conversely.

2. The correspondence is continuous in both directions. This means that if we take any two points p, q of A and move p so that the distance between it and q approaches zero, then the distance between the corresponding points p’, q’ of A’ will also approach zero, and conversely.

Any property of a geometrical figure A that holds as well for every figure into which A may be transformed by a topological transformation is called a topological property of A, and topology is the branch of geometry which deals only with the topological properties of figures. Imagine a figure to be copied “free-hand” by a conscientious but inexpert draftsman who makes straight lines curved and alters angles, distances and areas; then, although the metric and projective properties of the original figure would be lost, its topological properties would remain the same.

The most intuitive examples of general topological transformations are the deformations. Imagine a figure such as a sphere or a triangle to be made from or drawn upon a thin sheet of rubber, which is then stretched and twisted in any manner without tearing it and without bringing distinct points into actual coincidence. (Bringing distinct points into coincidence would violate condition 1. Tearing the sheet of rubber would violate condition 2, since two points of the original figure which tend toward coincidence from opposite sides of a line along which the sheet is torn would not tend towards coincidence in the torn figure.) The final position of the figure will then be a topological image of the original. A triangle can be deformed into any other triangle or into a circle or an ellipse, and hence these figures have exactly the same topological properties. But one cannot deform a circle into a line segment, nor the surface of a sphere into the surface of an inner tube.

Fig. 123. Topologically equivalent surfaces.

Fig. 124. Topologically non-equivalent surfaces.

The general concept of topological transformation is wider than the concept of deformation. For example, if a figure is cut during a deformation and the edges of the cut sewn together after the deformation in exactly the same way as before, the process still defines a topological transformation of the original figure, although it is not a deformation. Thus the two curves of Figure 134 (p. 256) are topologically equivalent to each other or to a circle, since they may be cut, untwisted, and the cut sewn up. But it is impossible to deform one curve into the other or into a circle without first cutting the curve.

Topological properties of figures (such as are given by Euler’s theorem and others to be discussed in this section) are of the greatest interest and importance in many mathematical investigations. They are in a sense the deepest and most fundamental of all geometrical properties, since they persist under the most drastic changes of shape.

2. Connectivity

As another example of two figures that are not topologically equivalent we may consider the plane domains of Figure 125. The first of these consists of all points interior to a circle, while the second consists of all points contained between two concentric circles. Any closed curve lying in the domain a can be continuously deformed or “shrunk” down to a single point within the domain. A domain with this property is said to be simply connected. The domain b is not simply connected. For example, a circle concentric with the two boundary circles and midway between them cannot be shrunk to a single point within the domain, since during this process the curve would necessarily pass over the center of the circles, which is not a point of the domain. A domain which is not simply connected is said to be multiply connected. If the multiply connected domain b is cut along a radius, as in Figure 126, the resulting domain is simply connected.

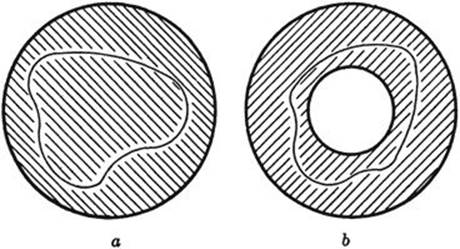
Fig. 125. Simple and double connectivity.

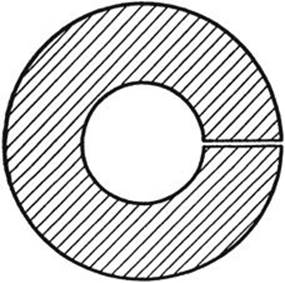
Fig. 126. Cutting a doubly connected domain to make it simply connected.

More generally, we can construct domains with two, three, or more “holes,” such as the domain of Figure 127. In order to convert this domain into a simply connected domain, two cuts are necessary. If n – 1 non-intersecting cuts from boundary to boundary are needed to convert a given multiply connected domain D into a simply connected domain, the domain D is said to be n-tuply connected. The degree of connectivity of a domain in the plane is an important topological invariant of the domain.

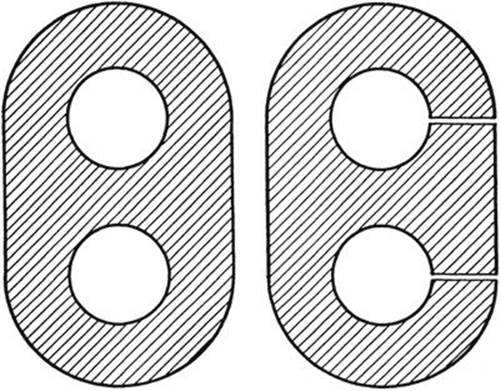
Fig. 127. Reduction of a triply connected domain.