What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

§2. LIMITS

1. The Limit of a Sequence a_n

As we have seen in §1, the description of the continuity of a function is based on the limit concept. Up to now we have used this concept in a more or less intuitive form. In this and the following sections we shall consider it in a more systematic way. Since sequences are rather simpler than functions of a continuous variable, we shall begin with a study of sequences.

In Chapter II we encountered sequences a_n of numbers and studied their limits as n increases indefinitely or “tends to infinity.” For example, the sequence whose nth term is a_n = 1/n,

has the limit 0 for increasing n:

Let us try to state exactly what is meant by this. As we go out farther and farther in the sequence, the terms become smaller and smaller. After the 100th term all the terms are smaller than 1/100, after the 1000th term all the terms are smaller than 1/1000, and so on. None of the terms is actually equal to 0. But if we go out far enough in the sequence (1), we can be sure that each of its terms will differ from 0 by as little as we please.

The only trouble with this explanation is that the meaning of the italicized phrases is not entirely clear. How far is “far enough,” and how little is “as little as we please”? If we can attach a precise meaning to these phrases then we can give a precise meaning to the limiting relation (2).

A geometric interpretation will help to make the situation clearer. If we represent the terms of the sequence (1) by their corresponding points on the number axis we observe that the terms of the sequence appear to cluster around the point 0. Let us choose any interval I on the number axis with center at the point 0 and total width 2ε, so that the interval extends a distance ε on each side of the point 0. If we choose ε = 10, then, of course, all the terms a_n = 1/n of the sequence will lie inside the interval I. If we choose ε = 1/10, then the first few terms of the sequence will lie outside I, but all the terms from a₁₁ on,

will lie within I. Even if we choose ε = 1/1000, only the first thousand terms of the sequence will fail to lie within I, while from the term a₁₀₀₁ on, all the infinitely many terms

a₁₀₀₁, a₁₀₀₂, a₁₀₀₃, · · ·

will lie within I. Clearly, this reasoning holds for any positive number ε: as soon as a positive ε is chosen, no matter how small it may be, we can then find an integer N so large that

From this it follows that all the terms a_n of the sequence for which n ≥ N will lie within I, and only the finite number of terms a₁, a₂, · · ·, a_N–1 can lie outside. The important point is this: First the width of the interval I is assigned at pleasure by choosing ε. Then a suitable integer N can be found. This process of first choosing a number ε and then finding a suitable integer N can be carried out for any positive number ε, no matter how small, and gives a precise meaning to the statement that all the terms of the sequence (1) will differ from 0 by as little as we please, provided we go out far enough in the sequence.

To summarize: Let ε be any positive number. Then we can find an integer N such that all the terms a_n of the sequence (1) for which n≥ N will lie within the interval I of total width 2ε and with center at the point 0. This is the precise meaning of the limiting relation (2).

On the basis of this example we are now ready to give an exact definition of the general statement: “The sequence of real numbers a₁, a₂, a₃,· · · has the limit a.” We include a in the interior of an interval I of the number axis: if the interval is small, some of the numbers a_n may lie outside the interval, but as soon as n becomes sufficiently large, say greater than or equal to some integer N, then all the numbers a_n for which n ≥ N must lie within the interval I. Of course, the integer N may have to be taken very large if a very small interval I is chosen, but no matter how small the interval I, such an integer N must exist if the sequence is to have a as its limit.

The fact that a sequence a_n has the limit a is expressed symbolically by writing

lim a_n = a asn → ∞,

or simply

a_n → a as n → ∞

(read: a_n tends to a, or converges to a). The definition of the convergence of a sequence a_n to a may be formulated more concisely as follows: The sequence a₁, a₂, a₃, · · · has the limit a as n tends to infinity if, corresponding to any positive number ε, no matter how small, there may be found an integer N (depending on ε), such that

(3) |a – a_n| < ε

for all

n ≥ N.

This is the abstract formulation of the notion of the limit of a sequence. Small wonder that when confronted with it for the first time one may not fathom it in a few minutes. There is an unfortunate, almost snobbish attitude on the part of some writers of textbooks, who present the reader with this definition without a thorough preparation, as though an explanation were beneath the dignity of a mathematician.

The definition suggests a contest between two persons, A and B. A sets the requirement that the fixed quantity a should be approached by a_n with a degree of accuracy better than a chosen margin ε = ε₁; B meets the requirement by demonstrating that there is a certain integer N = N₁ such that all the a_n after the element a_N1 satisfy the ε₁-requirement. Then A may become more exacting and set a new, smaller, margin, ε = ε₂. B again meets his demand by finding a (perhaps much larger) integer N = N₂. If B can satisfy A no matter how small A sets his margin, then we have the situation expressed by a_n → a.

There is a definite psychological difficulty in grasping this precise definition of limit. Our intuition suggests a “dynamic” idea of a limit as the result of a process of “motion”: we move on through the row of integers 1, 2, 3, · · ·, n, · · · and then observe the behavior of the sequence a_n. We feel that the approach a_n → a should be observable. But this “natural” attitude is not capable of clear mathematical formulation. To arrive at a precise definition we must reverse the order of steps; instead of first looking at the independent variable n and then at the dependent variable a_n, we must base our definition on what we have to do if we wish actually to check the statement a_n → a. In such a procedure we must first choose an arbitrarily small margin around a and then determine whether we can meet this condition by taking the independent variable n sufficiently large. Then, by giving symbolic names, ε and N, to the phrases “arbitrarily small margin” and “sufficiently large n,” we are led to the precise definition of limit.

As another example, let us consider the sequence

where . I state that lim a_n = 1. If you choose an interval whose center is the point 1 and for which ε = 1/10, then I can satisfy your requirement (3) by choosing N = 10; for

as soon as n ≥ 10. If you strengthen your demand by choosing ε = 1/1000, then again I can meet it by choosing N = 1000; and similarly for any positive number ε, no matter how small, which you may choose; in fact, I need only choose any integer N greater than 1/ε. This process of assigning an arbitrarily small margin ε about the number a and then proving that the terms of the sequence a_n are all within a distance ε of a if we go far enough out in the sequence, is the detailed description of the fact that lim a_n = a.

If the members of the sequence a₁, a₂, a₃, · · · are expressed as infinite decimals, then the statement lim a_n = a simply means that for any positive integer m the first m digits of a_n coincide with the first m digits of the infinite decimal expansion of the fixed number a, provided that n is chosen sufficiently large, say greater than or equal to some value N (depending on m). This merely corresponds to choices of ε of the form 10^–m.

There is another, quite suggestive, way of expressing the limit concept. If lim a_n = a, and if we enclose a in the interior of an interval I, then no matter how small I may be, all the numbers a_n for which n is greater than or equal to some integer N will lie within I, so that at most a finite number, N—1, of terms at the beginning of the sequence,

a₁, a₂,· · ·,a_N–1,

can lie outside I. If I is very small, N may be very large, say a hundred or even a thousand billion; still only a finite number of terms of the sequence will lie outside I, while the infinitely many remaining terms will lie within I.

We may say of the members of any infinite sequence that “almost all” have a certain property if only a finite number, no matter how great, do not have the property. For example “almost all” positive integers are greater than 1,000,000,000,000. Using this terminology, the statement lim a_n= a is equivalent to the statement: If I is any interval with a as its center, then almost all of the numbers a_n lie within I.

It should be noted in passing that it is not necessarily assumed that all the terms a_n of a sequence have different values. It is permissible for some, infinitely many, or even all the numbers a_n to be equal to the limit value a. For example, the sequence for which a₁ = 0, a₂ = 0, · · ·, a_n = 0, · · · is a legitimate sequence, and its limit, of course, is 0.

A sequence a_n with a limit a is called convergent. A sequence a_n without a limit is called divergent.

Exercises: Prove:

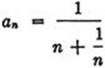1. The sequence for which has the limit 0. (Hint: is less than and greater than 0.)

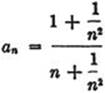2. The sequence has the limit 0. (Hint: lies between 0 and .)

3. The sequence 1, 2, 3, 4, · · · and the oscillating sequences

1, 2, 1, 2, 1, 2,· · ·,

–1, 1,–1, 1,–1, · · · (i.e. a_n = (–1)ⁿ),

and

do not have limits.

If in a sequence a_n the members become so large that eventually a_n is larger than any preassigned number K, then we say that a_n tends to infinity and write lim a_n = ∞, or a_n → ∞. For example, n² → ∞ and 2ⁿ → ∞. This terminology is useful, though perhaps not quite consistent, because ∞ is not considered to be a number a. A sequence tending to infinity is still called divergent.

Exercise: Prove that the sequence tends to infinity; similarly for , and .

Beginners sometimes fall into the error of thinking that a passage to the limit as n → ∞ may be performed simply by substituting n = ∞ in the expression for a_n. For example, 1/n → 0 because “1/∞ = 0.” But the symbol ∞ is not a number, and its use in the expression 1/∞ is illegitimate. Trying to imagine the limit of a sequence as the “ultimate” or “last” term a_n when n = ∞ misses the point and obscures the issue.

2. Monotone Sequences

In the general definition of page 291, no specific type of approach of a convergent sequence a₁, a₂, a₃, · · · to its limit a is required. The simplest type is exhibited by a so-called monotone sequence, such as the sequence

Each term of this sequence is greater than the preceding term. For . A sequence of this sort, where a_n+1 > a_n, is said to be monotone increasing. Similarly, a sequence for which a_n > a_n+1, such as the sequence 1, 1/2, 1/3, · · ·, is called monotone decreasing. Such sequences can approach their limits from one side only. In contrast to these, there are sequences that oscillate, such as the sequence –1, +1/2, –1/3, +1/4, ···. This sequence approaches its limit 0 from both sides (see Fig. 11, p. 69).

The behavior of a monotone sequence is especially easy to determine. Such a sequence may have no limit, but run away completely, like the sequence

1, 2, 3, 4, · · ·,

where a_n = n, or the sequence

2, 3, 5, 7, 11, 13, · · ·,

where a_n is the nth prime number, p_n. In this case the sequence tends to infinity. But if the terms of a monotone increasing sequence remain bounded—that is, if every term is less than an upper bound B, known in advance—then it is intuitively clear that the sequence must tend to a certain limit a which will be less than or at most equal to B. We formulate this as the Principle of Monotone Sequences: Any monotone increasing sequence that has an upper bound must converge to a limit. (A similar statement holds for any monotone decreasing sequence with a lower bound.) It is remarkable that the value of the limit need not be given or known in advance; the theorem states that under the prescribed conditions the limit exists. Of course, this theorem depends on the introduction of irrational numbers and would otherwise not always be true; for, as we have seen in Chapter II, any irrational number (such as ) is the limit of the monotone increasing and bounded sequence of rational decimal fractions obtained by breaking off a certain infinite decimal at the nth digit.

Fig. 166. Monotone bounded sequence.

* Although the principle of monotone sequences appeals to the intuition as an obvious truth, it will be instructive to give a rigorous proof in the modern fashion. To do this we must show that the principle is a logical consequence of the definitions of real number and limit.

Suppose that the numbers a₁, a₂, a₃,· · · form a monotone increasing but bounded sequence. We can express the terms of this sequence as infinite decimals,

a₁ = A₁.p₁p₂p₃ · · ·,

a₂ = A₂.q₁q₂q₃ · · ·,

a₃ = A₃.r₁r₂r₃ · · ·,

..............................

where the A_i are integers and the p_i, q_i, etc. are digits from 0 to 9. Now run down the column of integers A₁, A₂, A₃, · · ·. Since the sequence a₁, a₂, a₃, · · · is bounded, these integers cannot increase indefinitely, and since the sequence is monotone increasing, the sequence of integers A₁, A₂,A₃, · · · will remain constant after attaining its maximum value. Call this maximum value A, and suppose that it is attained at the N₀th row. Now run down the second column p_1,, q₁, r₁, · · ·, confining attention to the terms of the N_oth and subsequent rows. If x₁ is the largest digit to appear in this column after the N_oth row, then x₁ will appear constantly after its first appearance, which we may suppose to occur in the N₁th row, where N₁ ≥ N_o. For if the digit in this column decreased at any time thereafter, the sequence a₁, a₂, a₃, · · · would not be monotone increasing. Next we consider the digits p_2,, q₂, r₂, · · · of the third column. A similar argument shows that after a certain integer N₂ ≥ N₁ the digits of the third column are constantly equal to some digit x₂. If we repeat this process for the 4th, 5th, · · · columns we obtain digits x₃, x₄, x₅, · · · and corresponding integers N₃, N₄, N₅, · · ·. It is easy to see that the number

a = A.x₁x₂x₃x₄ · · ·

is the limit of the sequence a₁, a₂, a₃, · · ·. For if ε is chosen ≥ 10^–m, then for all n ≥ N_m the integral part and first m places of digits after the decimal point in a_n will coincide with those of a, so that the difference | a – a_n | cannot exceed 10^–m. Since this can be done for any positive ε, however small, by choosing m sufficiently large, the theorem is proved.

It is also possible to prove this theorem on the basis of any one of the other definitions of real numbers given in Chapter II; for example, the definition by nested intervals or by Dedekind cuts. Such proofs are to be found in most texts on advanced calculus.

The principle of monotone sequences could have been used in Chapter II to define the sum and product of two positive infinite decimals,

a = A.a₁ a₂ a₃ · · ·,

b = B.b₁ b₂ b₃ · · ·.

Two such expressions cannot be added or multiplied in the ordinary way, starting from the right-hand end, for there is no such end. (As an example, the reader may try to add the two infinite decimals 0.333333 · · ·and 0.989898 · · ·.) But if x_n denotes the finite decimal fraction obtained by breaking off the expressions for a and b at the nth place and adding in the ordinary way, then the sequence x₁, x₂, x₃,· · · will be monotone increasing and bounded (by the integer A + B + 2, for example). Hence this sequence has a limit, and we may define a + b = lim x_n. A similar process serves to define the product ab. These definitions can then be extended by the ordinary rules of arithmetic to cover all cases, where a and b are positive or negative.

Exercise: Show in this way that the sum of the two infinite decimals considered above is the real number 1.323232 · · · = 131/99.

The importance of the limit concept in mathematics lies in the fact that many numbers are defined only as limits—often as limits of monotone bounded sequences. This is why the field of rational numbers, in which such limits may not exist, is too narrow for the needs of mathematics.

3. Euler’s Number e

The number e has had an established place in mathematics alongside the Archimedean number π ever since the publication in 1748 of Euler’s Introductio in Analysin Infinitorum. It provides an excellent illustration of how the principle of monotone sequences can serve to define a new real number. Using the abbreviation

n! = 1.2.3.4 · · · n

for the product of the first n integers, we consider the sequence a₁, a₂, a₃, · · ·, where

The terms a_n form a monotone increasing sequence, since a_n+1 originates from a_n by the addition of the positive increment . Moreover, the values of a_n are bounded above:

(5)  a_n B < = 3.

For we have

and hence

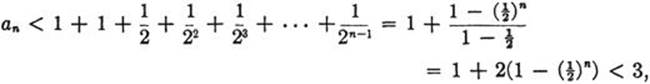
using the formula given on page 13 for the sum of the first n terms of a geometric series. Hence, by the principle of monotone sequences, a_n must approach a limit as n tends to infinity, and this limit we call e. To express the fact that e = lim a_n, we may write e as the “infinite series”

(6)  

This “equality,” with a row of dots at the end, is simply another way of expressing the content of the two statements

and

a_n → e as n → ∞.

The series (6) permits the calculation of e to any desired degree of accuracy. For example, the sum (to nine digits) of the terms in (6) up to and including 1/12! is Σ = 2.71828183 · · ·. (The reader should check this result.) The “error,” i.e. the difference between this value and the true value of e can easily be appraised. We have for the difference (e – Σ) the expression

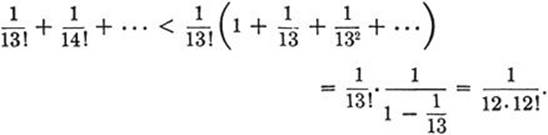
This is so small that it cannot affect the ninth digit of Σ. Hence, allowing for a possible error in the last figure of the value given above, we have e = 2.7182818, to eight digits.

* The number e is irrational. To prove this we shall proceed indirectly by assuming that e = p/q, where p and q are integers, and then deducing an absurdity from this assumption. Since we know that 2 < e < 3, e cannot be an integer, and therefore q must be at least equal to 2. Now we multiply both sides of (6) by q! = 2.3 · · · q, obtaining

(7)

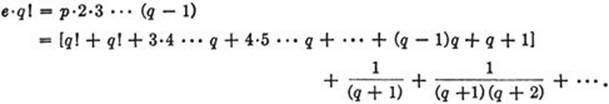
On the left side we obviously have an integer. On the right side, the term in brackets is likewise an integer. The remainder of the right side, however, is a positive number that is less than and hence no integer. For q ≥ 2, and hence the terms of the series 1/(q + 1) + · · · are respectively not greater than the corresponding terms of the geometrical series 1/3 + 1/3² + 1/3³ + · · ·, whose sum is . Hence (7) presents a contradiction: the integer on the left side cannot be equal to the number on the right side; for this latter number, being the sum of an integer and a positive number less than , is not an integer.

4. The Number π

As is known from school mathematics, the length of the circumference of a circle of unit radius can be defined as the limit of a sequence of lengths of regular polygons with an increasing number of sides. The length of the circumference so defined is denoted by 2π. More precisely, if p_ndenotes the length of the inscribed, and q_n the length of the circumscribed regular n-sided polygon, then p_n < 2π < q_n. Moreover, as n increases, each of the sequences p_n, q_n approaches 2π monotonically, and with each step we obtain a smaller margin for the error in the approximation of 2π given by p_n or q_n.

On page 124 we found the expression

containing m – 1 nested square root signs. This formula can be used to compute the approximate value of 2π.

Fig. 167. Circle approximated by polygons.

Exercises: 1. Find the approximate value of π given by p₄, p₈, and p₁₆.

* 2. Find a formula for q2^m.

* 3. Use this formula to find q₄, q₈, and q₁₆.

From a knowledge of p₁₆ and q₁₆, state bounds between which π must lie.

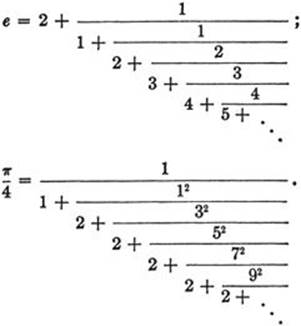
What is the number π? The inequality p_n < 2π < q_n gives the complete answer by setting up a sequence of nested intervals which close down on the point 2π. Still, this answer leaves something to be desired, for it gives no information about the nature of π as a real number: is it rational or irrational, algebraic or transcendental? As we have mentioned on page 140, π is in fact a transcendental number, and hence irrational. In contrast to the proof for e, the proof of the irrationality of π, first given by J. H. Lambert (1728-1777), is rather difficult and will not be undertaken here. However, other information about π is within our reach. Recalling the statement that the integers are the basic material of mathematics, we may ask whether the number π has any simple relationship to the integers. The decimal expansion of π, although it has been calculated to several hundred places, reveals no trace of regularity. This is not surprising, since π and 10 have nothing to do with one another. But in the eighteenth century Euler and others found beautiful expressions linking π to the integers by means of infinite series and products. Perhaps the simplest such formula is the following:

expressing π/4 as the limit for increasing n of the partial sums

We shall derive this formula in Chapter VIII. Another infinite series for π is

Still another striking expression for π was discovered by the English mathematician John Wallis (1616-1703). His formula states that

This is sometimes written in the abbreviated form

the expression on the right being called an infinite product.

A proof of the last two formulas will be found in any comprehensive book on the calculus (see p.482 and pp. 509-510).

*5. Continued Fractions

Interesting limiting processes occur in connection with continued fractions. A finite continued fraction, such as

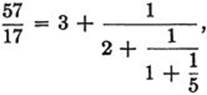
represents a rational number. On page 49 we showed that every rational number can be written in this form by means of the Euclidean algorithm. For irrational numbers, however, the algorithm does not stop after a finite number of steps. Instead, it leads to a sequence of fractions of increasing length, each representing a rational number. In particular, all real algebraic numbers (see p. 103) of degree 2 may be expressed in this way. Consider, for example, the number , which is a root of the quadratic equation

If on the right side x is again replaced by 1/(2 + x) this yields the expression

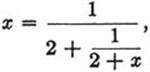
and then

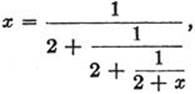
and so on, so that after n steps we obtain the equation

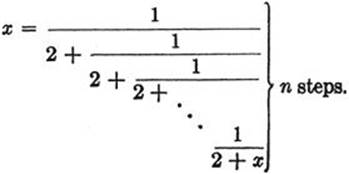
As n tends to infinity, we obtain the “infinite continued fraction”

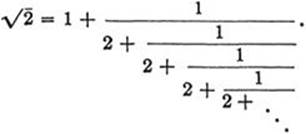
This remarkable formula connects with the integers in a much more striking way than does the decimal expansion of , which displays no regularity in the succession of its digits.

For the positive root of any quadratic equation of the form

we obtain the expansion

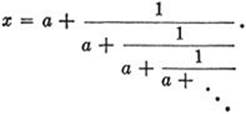
For example, setting a = 1, we find

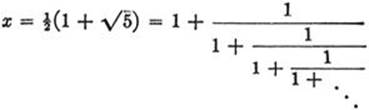
(cf. p. 123). These examples are special cases of a general theorem which states that the real roots of quadratic equations with integral coefficients have periodic continued fraction developments, just as rational numbers have periodic decimal expansions.

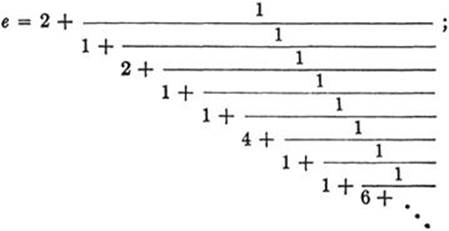
Euler was able to find almost equally simple infinite continued fractions for e and π. The following are exhibited without proof: