What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

INTRODUCTION

A straight segment is the shortest connection between its endpoints. An arc of a great circle is the shortest curve joining two points on a sphere. Among all closed plane curves of the same length the circle encloses the largest area, and among all closed surfaces of the same area the sphere encloses the largest volume.

Maximum and minimum properties of this type were known to the Greeks, even though the results were often stated without a real attempt at a proof. One of the most significant Greek discoveries is ascribed to Heron, the Alexandrian scientist of the first century A.D. It had long been known that a light ray from a point P meeting a plane mirror L in a point R is reflected in the direction of a point Q such that PR and QR form equal angles with the mirror. Heron found that if R′ is any other point on the mirror, then the total distance PR′ + R′Q is larger than the distance PR + RQ. This theorem, which we shall prove presently, characterizes the actual path of light PRQ between P and Q as the shortest possible path from P to Q by way of the mirror— a discovery that can be considered the germ of the theory of geometrical optics.

It is only natural that mathematicians should be interested in questions of this sort. In daily life problems of maxima and minima, of the “best” and the “worst,” arise constantly. Many problems of practical importance present themselves in this form. For example, how should a boat be shaped so as to have the least possible resistance in water? What cylindrical container made from a given amount of material has a maximum volume?

Starting in the seventeenth century, the general theory of extreme values—maxima and minima—has become one of the systematic integrating principles of science. Fermat’s first steps in his differential calculus were prompted by the desire to study questions of maxima and minima by general methods. In the century that followed, the scope of these methods was greatly widened by the invention of the “calculus of variations.” It became increasingly apparent that the physical laws of nature are most adequately expressed in terms of a minimum principle that provides a natural access to a more or less complete solution of particular problems. One of the most remarkable achievements of contemporary mathematics is the theory of stationary values—an extension of the notion of extreme values which combines analysis and topology. Our approach to the whole subject will be quite elementary.

§1. PROBLEMS IN ELEMENTARY GEOMETRY

1. Maximum Area of a Triangle with Two Sides Given

Given two segments a and b; required to find the triangle of maximum area having a and b as sides. The solution is simply the right triangle whose two legs are a and b. For consider any triangle with a and b as sides, as in Figure 176. If h is the altitude on the base a, then the area of the triangle is . Now is clearly a maximum when h is largest, and this occurs when h coincides with b; that is, for a right triangle. Hence the maximum area is .

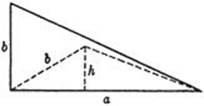
Fig. 176.

2. Heron’s Theorem. Extremum Property of Light Rays

Given a line L and two points P and Q on the same side of L. For what point R on L is PR + RQ the shortest path from P to L to Q? This is Heron’s problem of the light ray. (If L were the bank of a stream, and someone had to go from P to Q as fast as possible, fetching a pail of water from L on the way, then he would have to solve just this problem.) To find the solution, we reflect P in L as in a mirror, obtaining the point P′ such that L is the perpendicular bisector of PP′. The line P′Q intersects L in the required point R. It is simple to prove that PR + RQ is smaller thanPR′ + R′Q for any other point R’ on L. For PR = P′R and PR′ = P′R′; hence, PR + RQ = P′R + RQ = P′Q and PR′ + R′Q = P′R′ + R′Q. But P′R′ + R′Q is greater than P′Q (since the sum of any two sides of a triangle is greater than the third side), hence PR′ + R′Q is greater than PR + RQ, which was to be proved. In what follows we assume that neither P nor Q lies on L.

From Figure 177 we see that 3 = 2, and 2 = 1, so that 1 = 3. In other words, R is the point such that PR and QR make equal angles with L. From this it follows that a light ray reflected in L (which is known from experiment to make equal angles of incidence and reflection) actually takes the shortest path from P to L to Q, as stated above in the introduction.

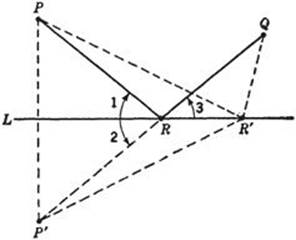
Fig. 177. Heron’s theorem.

The problem can be generalized to include several lines L, M, · · ·. For example, consider the case where we have two lines L, M and two points P, Q situated as in Figure 178, with the problem of finding the path of minimum length from P to L, then to M, then to Q. Let Q′ be the reflection of Q in M and Q” the reflection of Q’ in L. Draw PQ” intersecting L in R and RQ′ intersecting M in S; then R and S are the required points such that PR + RS + SQ is the path of minimum length from P to L to M to Q. The proof of this fact is very similar to that of the previous problem, and is left as an exercise for the reader. If L and M were mirrors, a light ray from P, reflected from L to M, and there reflected to Q, would meet L at R and M at S; hence the light ray would again take the path of shortest length.

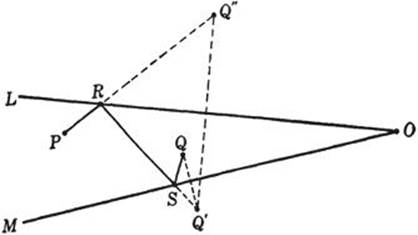
Fig. 178. Reflection in two mirrors.

One might ask for the shortest path first from P to M, then to L, and from there to Q. This would give a path PRSQ (see Fig. 179) determined in a manner similar to the previous path PRSQ. The length of the first path may be greater than, equal to, or less than that of the second.

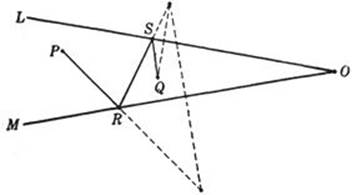
Fig. 179.

* Exercise: Show that the first path is smaller than the second if O and R lie on the same side of the line PQ. When will the two paths be of equal length?

3. Applications to Problems on Triangles

With the help of Heron’s theorem solutions to the following two problems are easily obtained.

a) Given the area A and one side c = PQ of a triangle; among all such triangles to determine the one for which the sum of the other sides a and b is smallest. Prescribing the side c and the area A of a triangle is equivalent to prescribing the side c and the altitude h on c, since . Referring to Figure 180, the problem is therefore to find a point R such that the distance from R to the line PQ is equal to the given h, and such that the sum a + b is a minimum. From the first condition it follows that R must lie on the line parallel to PQ at a distance h. The answer is given by Heron’s theorem for the special case where P and Q are equally distant from L: the required triangle PRQ is isosceles.

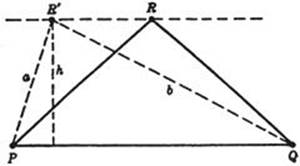
Fig. 180. Triangle of minimum perimeter with given base and area.

b) In a triangle let one side c and the sum a + b of the two other sides be given; to find among all such triangles the one with the largest area. This is just the converse of problem a). The solution is again the isosceles triangle for which a = b. As we have just shown, this triangle has the minimum value of a + b for its area; that is, any other triangle with the base c and the same area has a greater value of a + b. Moreover, it is clear from a) that any triangle with base c and an area greater than that of the isosceles triangle also has a greater value of a + b. Hence any other triangle with the same values of a + b and of c must have a smaller area, so that the isosceles triangle provides the maximum area for given c and a + b.

4. Tangent Properties of Ellipse and Hyperbola. Corresponding Extremum Properties

The problem of Heron is connected with some important geometrical theorems. We have proved that if R is the point on L such that PR + RQ is a minimum, then PR and RQ make equal angles with L. This minimum total distance we shall call 2a. Let p and q denote the distances from any point in the plane to P and Q respectively, and consider the locus of all points in the plane for which p + q = 2a. This locus is an ellipse, with P and Q as foci, that passes through the point R on the line L. Moreover, L must be tangent to the ellipse at R. If L intersected the ellipse at a point other than R, there would be a segment of L lying inside the ellipse; for each point of this segment p + q would be less than 2a, since it is easily seen that p + q is less than 2a inside the ellipse and greater than 2a outside. Since we know that p + q ≥ 2a on L, this is impossible. Hence L must be tangent to the ellipse at R. But we know that PR and RQ make equal angles with L; hence we have incidentally proved the important theorem: A tangent to an ellipse makes equal angles with the lines joining the foci to the point of tangency.

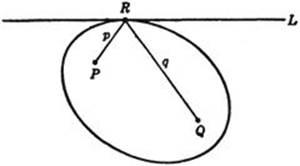
Fig. 181. Tangent property of ellipse.

Closely related to the foregoing discussion is the following problem: Given a straight line L and two points P and Q on opposite sides of L (see Fig. 182), to find a point R on L such that the quantity | p – q |, that is, the absolute value of the difference of the distances from P and Q to R, is a maximum. (We shall assume that L is not the perpendicular bisector of PQ; for then p – q would be zero for every point R on L and the problem would be meaningless.) To solve this problem, we first reflect P in L, obtaining the point P′ on the same side of L as Q. For any point R′ on L, we have p = R′P = R′P′, q = R′Q. Since R′, Q, and P′ can be regarded as the vertices of a triangle, the quantity | p – q | = | R′P′ – R′Q | is never greater than P′Q, for the difference between two sides of a triangle is never greater than the third side. If R′, P′, and Q all lie on a straight line, | p – q | will be equal to P′Q, as is seen from the figure. Therefore the desired point R is the intersection of L with the line through P′ and Q. As in the previous case, it is easily seen that the angles which RP and RQ make with L are equal, since the triangles RPR′ and RP′R′ are congruent.

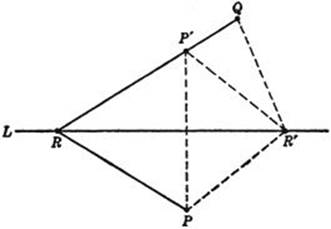
Fig. 182. | PR – QR | = maximum.

This problem is connected with a tangent property of the hyperbola, just as the preceding one was connected with the ellipse. If the maximum difference | PR — QR | has the value 2a, we can consider the locus of all points in the plane for which p – q has the absolute value 2a. This is a hyperbola with P and Q as its foci and passing through the point R. As is easily shown, the absolute value of p – q is less than 2a in the region between two branches of the hyperbola, and greater than 2a on that side of each branch where the corresponding focus lies. It follows, by essentially the same argument as for the ellipse, that L must be tangent to the hyperbola at R. Which of the two branches is touched by L depends on whether P or Q is nearer to L; if P is nearer, the branch surrounding P will touch L, and likewise for Q (see Fig. 183).

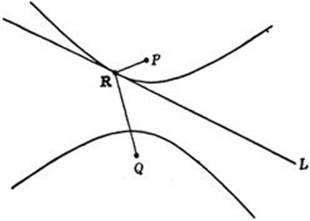
Fig. 183. Tangent property of hyperbola.

If P and Q are equidistant from L, then L will touch neither branch of the hyperbola, but will, instead, be one of the curve’s asymptotes. This result becomes plausible when one observes that for this case the preceding construction will yield no (finite) point R, since the line P′Q will be parallel to L.

In the same way as before this argument proves the well known theorem: A tangent to a hyperbola at any point bisects the angle subtended at that point by the foci of the hyperbola.

It may seem strange that if P and Q are on the same side of L we have a minimum problem to solve, while if they are on opposite sides of L we considered a maximum problem. That this is natural can be seen at once. In the first problem, each of the distances p, q, and therefore their sum, becomes larger without bound as we proceed along L indefinitely in either direction. Hence it would be impossible to find a maximum value for p + q, and a minimum problem is the only possibility. It is quite different in the second case, where P and Q lie on different sides of L. Here, to avoid confusion, we have to distinguish between the difference p – q, its negative q – p, and the absolute value | p – q |; it is the latter which was made a maximum. The situation is best understood if we let the point R move along the line L through different positions, R₁, R₂, R₃, · · ·. There is one point for which the difference p – q is zero: the intersection of the perpendicular bisector of PQ with L. This point therefore gives a minimum for the absolute value | p – q|. But on one side of this point p is greater than q, and on the other, less; hence the quantity p – q is positive on one side of the point and negative on the other. Consequently p – q itself is neither a maximum nor a minimum at the point for which | p – q | = 0. However, the point making | p – q | a maximum is actually an extremum of p – q. If p > q, we have a maximum for p – q; if q > p, a maximum for p –q and hence a minimum for p – q. Whether a maximum or a minimum for p – q is obtainable is determined by the position of the two given points P, Q relative to the line L.

We have seen that no solution of the maximum problem exists if P and Q are equidistant from L, since then the line P′Q in Figure 182 is parallel to L. This corresponds to the fact that the quantity | p – q | tends to a limit as R tends to infinity along L in either direction. This limiting value is equal to the length of the perpendicular projection s of PQ on L (the reader may prove this as an exercise). If P and Q have the same distance from L, then | p – q | will always be less than this limit and no maximum exists, since to each point R we can find another farther out for which | p –q | is larger, but still not quite equal to s.

*5. Extreme Distances to a Given Curve

First we shall determine the shortest and the longest distance from a point P to a given curve C. For simplicity we shall suppose that C is a simple closed curve with a tangent everywhere, as in Figure 184. (The concept of tangent to a curve is here accepted on an intuitive basis that will be analyzed in the next chapter.) The answer is very simple: A point R on C for which the distance PR has its smallest or its largest value must be such that the line PR is perpendicular to the tangent to C at R; in other words, PR is perpendicular to C. The proof is as follows: the circle with center at P and passing through R must be tangent to the curve. For if R is the point of minimum distance, C must lie entirely outside the circle, and therefore cannot cross it at R, while if R is the point of maximum distance, C must lie entirely inside the circle, and again cannot cross it at R. (This follows from the obvious fact that the distance from any point to P is less than RP if the point lies inside the circle, and greater than RP if the point lies outside the circle.) Hence the circle and the curve C will touch and have a common tangent at R. Now the line PR, being a radius of the circle, is perpendicular to the tangent to the circle at R, and therefore perpendicular to C at R.

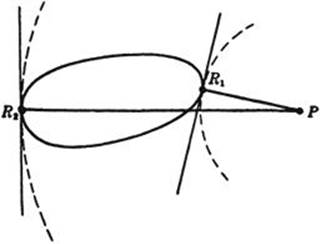
Fig. 184. Extreme distances to a curve.

Incidentally, the diameter of such a closed curve C, that is, its longest chord, must be perpendicular to C at both endpoints. The proof is left as an exercise for the reader. A similar statement should be formulated and proved in three dimensions.

Exercise: Prove that the shortest and longest segments connecting two nonintersecting closed curves are perpendicular to the curves at their endpoints.

The problems in Article 4 concerning the sum or difference of distances can now be generalized. Consider, instead of a straight line L, a simple closed curve C with a tangent at every point, and two points, P and Q, not on C. We wish to characterize the points on C for which the sum, p +q, and the difference, p – q, take on their extreme values, where p and q denote the distances from any point on C to P and Q respectively. No use can be made of the simple construction of reflection with which we solved the problems for the case where C is a straight line. But we may use the properties of the ellipse and hyperbola to solve the present problems. Since C is a closed curve and no longer a line extending to infinity, both the minimum and maximum problems make sense here, for it may be taken as granted that the quantities p + q and p – q have greatest and least values on any finite segment of a curve, in particular on a closed curve (see §7).

For the case of the sum, p + q, suppose R is the point on C for which p + q is a maximum, and let 2a denote the value of p + q at R. Consider the ellipse with foci at P and Q that is the locus of all points for which p + q = 2a. This ellipse must be tangent to C at R (the proof is left as an exercise for the reader). But we have seen that the lines PR and QR make equal angles with the ellipse at R; since the ellipse is tangent to C at R, the lines PR and QR must also make equal angles with C at R. If p + q is a minimum for R, we see in the same way that PR and QR make equal angles with C at R. Thus we have the theorem: Given a closed curve C and two points P and Q on the same side of C; then at a point R of C where the sum p + q takes on its greatest or least value on C, the lines PR and QR make equal angles with the curve C (i.e. with its tangent) at R.

If P is inside C and Q outside, this theorem also holds for the greatest value of p + q, but fails for the least value, since the ellipse degenerates into a straight line.

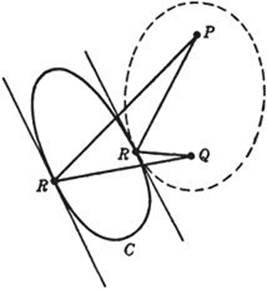
Fig. 185. Greatest and least values of PR + QR.

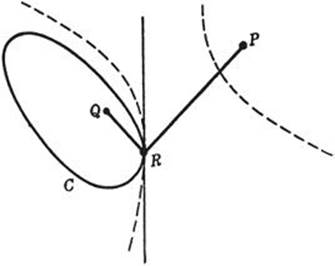
Fig. 186. Least value of PR – QR.

By an entirely analogous procedure, making use of properties of the hyperbola instead of the ellipse, the reader may prove the following theorem: Given a closed curve C and two points P and Q, on different sides of C; then at a point R of C where p – q takes on its greatest or least value on C, the lines PR and QR make equal angles with C. Again we emphasize that the problem for a closed curve C differs from that for an infinite line inasmuch as in the latter problem the maximum of the absolute value | p – q | was sought while now a maximum (as well as a minimum) of p –q exits.