What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

§4. SCHWARZ’S TRIANGLE PROBLEM

1. Schwarz’s Proof

Hermann Amandus Schwarz (1843-1921) was a distinguished mathematician of the University of Berlin and one of the great contributors to modern function theory and analysis. He did not disdain to write on elementary subjects, and one of his papers treats the following problem: Given an acute-angled triangle, to inscribe in it another triangle with the least possible perimeter. (By an inscribed triangle we mean one with a vertex on each side of the original triangle.) We shall see that there is exactly one such triangle, and that its vertices are the foot-points of the altitudes of the given triangle. We shall call this triangle the altitude triangle.

Schwarz proved the minimum property of the altitude triangle by the method of reflection, with the help of the following theorem of elementary geometry (see Fig. 197): At each vertex, P, Q, R, the two sides of the altitude triangle make equal angles with the side of the original triangle; this angle is equal to the angle at the opposite vertex of the original triangle. For example, the angles ARQ and BRP are both equal to angle C, etc.

To prove this preliminary theorem, we note that OPBR is a quadrilateral that can be inscribed in a circle, since OPB and ORB are right angles. Consequently, PBO = PRO, since they subtend the same are PO in the circumscribed circle. Now PBO is complementary to C, since CBQ is a right triangle, and PRO is complementary to PRB. Therefore the latter is equal to C. In the same way, using the quadrilateral QORA, we see that QRA = C, etc.

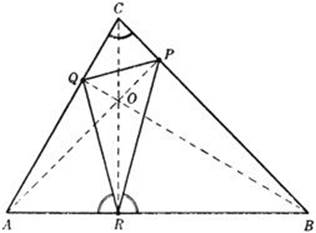
Fig. 197. Altitude triangle of ABC, showing equal angles.

This result enables us to state the following reflection property of the altitude triangle: Since, for example AQR = CQP, the reflection of RQ in the side AC is the continuation of PQ, and vice versa; similarly for the other sides.

We shall now prove the minimum property of the altitude triangle. In the triangle ABC consider, together with the altitude triangle, any other inscribed triangle, UVW. Reflect the whole figure first in the side AC of ABC, then reflect the resulting triangle in its side AB then in BC then again in AC, and finally in AB. In this way we obtain altogether six congruent triangles, each with the altitude triangle and the other one inscribed. The side BC of the last triangle is parallel to the original side BC. For in the first reflection, BC is rotated clockwise through an angle 2C, then through2B clockwise; in the third reflection it is not affected, in the fourth it rotates through 2C counterclockwise, and in the fifth through 2B counterclockwise. Thus the total angle through which it has turned is zero.

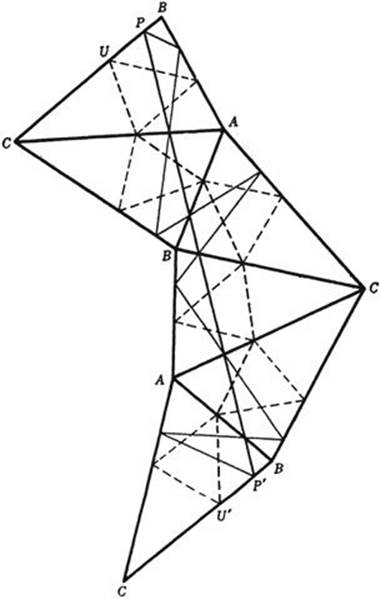
Fig. 198. Schwarz’s proof that altitude triangle has least perimeter.

Due to the reflection property of the altitude triangle, the straight line segment PP′ is equal to twice the perimeter of the altitude triangle; for PP′ is composed of six pieces that are, in turn, equal to the first, second, and third side of the triangle, each side occurring twice. Similarly, the broken line from U to U′ is twice the perimeter of the other inscribed triangle. This line is not shorter than the straight line segment UU′. Since UU′ is parallel to PP′, the broken line from U to U′ is not shorter than PP′, and therefore the perimeter of the altitude triangle is the shortest possible for any inscribed triangle, as was to be proved. Thus we have at the same time shown that there is a minimum and that it is given by the altitude triangle. That there is no other triangle with perimeter equal to that of the altitude triangle will be seen presently.

2. Another Proof

Perhaps the simplest solution of Schwarz’s problem is the following, based on the theorem proved earlier in this chapter that the sum of the distances from two points P and Q to a line L is least at that point R of L where PR and QR make the same angle with L, provided that P and Q lie on the same side of L and neither lies on L. Assume that the triangle PQR inscribed in the triangle ABC solves the minimum problem. Then R must be the point on the side AB where p + q is a minimum, and therefore the angles ARQ and BRP must be equal; similarly, . Thus the minimum triangle, if it exists, must have the equal-angle property used in Schwarz’s proof. It remains to be shown that the only triangle with this property is the altitude triangle. Moreover, since in the theorem on which this proof is based it is assumed that P and Q do not lie on AB, the proof does not hold in case one of the points P, Q, R is a vertex of the original triangle (in which case the minimum triangle would degenerate into twice the corresponding altitude); in order to complete the proof we must show that the perimeter of the altitude triangle is shorter than twice any altitude.

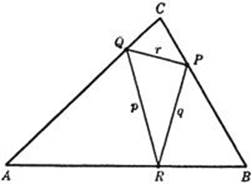
Fig. 199.

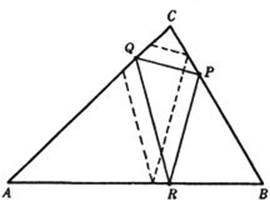
Fig. 200.

To dispose of the first point, we observe that if an inscribed triangle has the equal-angle property mentioned above, the angles at P, Q, and R must be equal to A, B, and C respectively. For assume, say, that ARQ = C + δ. Then, since the sum of the angles of a triangle is 180°, the angle at Q must be B – δ, and at P, A – δ, in order that the triangles ARQ and BRP may have the sum of their angles equal to 180°. But then the sum of the angles of the triangle CPQ is A – δ + B – δ + C = 180° – 2δ; on the other hand, this sum must be 180°. Therefore δ is equal to zero. We have already seen that the altitude triangle has this equal-angle property. Any other triangle with this property would have its sides parallel to the corresponding sides of the altitude triangle; in other words, it would have to be similar to it and oriented in the same way. The reader may show that no other such triangle can be inscribed in the given triangle (see Fig. 200).

Finally, we shall show that the perimeter of the altitude triangle is less than twice any altitude, provided the angles of the original triangle are all acute. We produce the sides QP and QR and draw the perpendiculars from B to QP, QR, and PR, thus obtaining the points L, M, and N. ThenQL and QM are the projections of the altitude QB on the lines QP and QR respectively. Consequently, QL + QM < 2QB. Now QL + QM equals p, the perimeter of the altitude triangle. For triangles MRB and NRB are congruent, since angles MRB and NRB are equal, and the angles at M andN are right angles. Hence RM = RN; therefore QM = QR + RN. In the same way, we see that PN = PL, so that QL = QP + PN. We therefore have QL + QM = QP + QR + PN + NR = QP + QR + PR = p. But we have shown that 2QB > QL + QM. Therefore p is less than twice the altitudeQB; by exactly the same argument, p is less than twice any altitude, as was to be proved. The minimum property of the altitude triangle is thus completely proved.

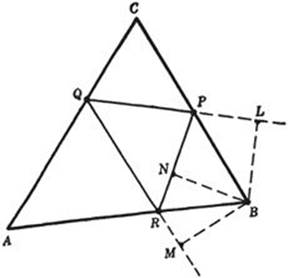
Fig. 201.

Incidentally, the preceding construction permits the direct calculation of p. We know that the angles PQC and RQA are equal to B, and therefore PQB = RQB = 90° – B, so that cos (PQB) = sin B. Therefore, by elementary trigonometry, QM = QL = QB sin B, and p = 2QB sin B. In the same way, it can be shown that p = 2PA sin A = 2RC sin C. From trigonometry, we know that RC = a sin B = b sin A, etc., which gives p = 2a sin B sin C = 2b sin C sin A = 2c sin A sin B. Finally, since a = 2r sin A, b = 2r sin B, c = 2r sin C, where r is the radius of the circumscribed circle, we obtain the symmetrical expression, p = 4r sin A sin B sin C.

3. Obtuse Triangles

In both of the foregoing proofs it has been assumed that the angles A, B, and C are all acute. If, say, C is obtuse, as in Figure 202, the points P and Q will lie outside the triangle. Therefore the altitude triangle can no longer, strictly speaking, be said to be inscribed in the triangle, unless by an inscribed triangle we merely mean one whose vertices are on the sides or on the extensions of the sides of the original triangle. At any rate, the altitude triangle does not now give the minimum perimeter, for PR > CR and QR > CR; hence p = PR + QR + PQ > 2CR. Since the reasoning in the first part of the last proof showed that the minimum perimeter, if not given by the altitude triangle, must be twice an altitude, we conclude that for obtuse triangles the “inscribed triangle” of smallest perimeter is the shortest altitude counted twice, although this is not properly a triangle. Still, one can find a proper triangle whose perimeter differs from twice the altitude by as little as we please. For the boundary case, the right triangle, the two solutions–twice the shortest altitude, and the altitude triangle—coincide.

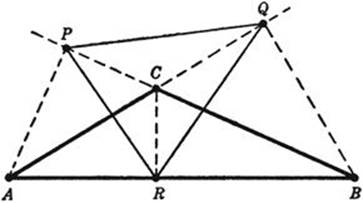
Fig. 202. Altitude triangle for obtuse triangle.

The interesting question whether the altitude triangle has any sort of extremum property for obtuse triangles cannot be discussed here. Only this much may be stated: the altitude triangle gives, not a minimum for the sum of the sides, p + q + r, but a stationary value of minimax type for the expression p + q – r, where r denotes the side of the inscribed triangle opposite the obtuse angle.

4. Triangles Formed by Light Rays

If the triangle ABC represents a chamber with reflecting walls, then the altitude triangle is the only triangular light path possible in the chamber. Other closed light paths in form of polygons are not excluded, as Figure 203 shows, but the altitude triangle is the only such polygon with three sides.

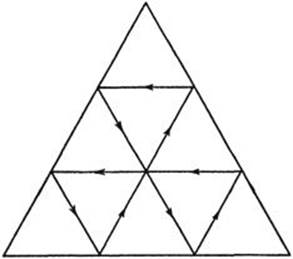
Fig. 203. Closed light path in a triangular mirror.

We may generalize this problem by asking for the possible “light triangles” in an arbitrary domain bounded by one or even several smooth curves; i.e. we ask for triangles with their vertices somewhere on the boundary curves and such that each two adjacent edges form the same angle with the curve. As we have seen in §1, the equality of angles is a condition for maximum as well as minimum total length of the two edges, so that we may, according to circumstances, find different types of light triangles. For example, if we consider the interior of a single smooth curve C, then the inscribed triangle of maximum length must be a light triangle. Or we may consider (as suggested to the authors by Marston Morse) the exterior of three smooth closed curves. A light triangle ABC may be characterized by the fact that its length has a stationary value; this value may be a minimum with respect to all three points A, B, C, it may be a minimum with respect to any of the combinations such as A and B and a maximum with respect to the third point C, it may be a minimum with respect to one point and a maximum with respect to the two others, or finally it may be a maximum with respect to all three points. Altogether the existence of at least 2³ = 8 light triangles is assured, since for each of the three points independently either a maximum or a minimum is possible.

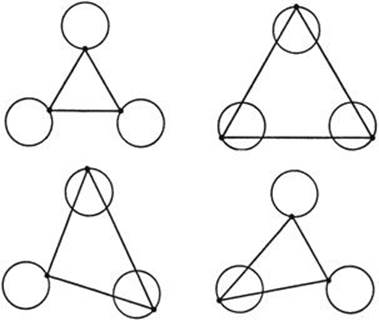
Figs. 204-7. The four types of light triangles between three circles.

*5. Remarks Concerning Problems of Reflection and Ergodic Motion

It is a problem of major interest in dynamics and optics to describe the path or “trajectory” of a particle in space or of a light ray for an unlimited length of time. If by some physical device the particle or ray is restricted to a bounded portion of space, it is of particular interest to know whether the trajectory will, in the limit, fill the space everywhere with an approximately equal distribution. Such a trajectory is called ergodic. The assumption of its existence is basic for statistical methods in modern dynamics and atomic theory. But very few relevant instances are known where a rigorous mathematical proof of the “ergodic hypothesis” can be given.

The simplest examples refer to the case of motion within a plane curve C, where the wall C is supposed to act as a perfect mirror, reflecting the otherwise free particle at the same angle at which it hits the boundary. For example, a rectangular box (an idealized billiard table with perfect reflection and a mass point as billiard ball) leads in general to an ergodic path; the ideal billiard ball going on for ever will reach the vicinity of every point, except for certain singular initial positions and directions. We omit the proof, although it is not difficult in principle.

Of particular interest is the case of an elliptical table with the foci F₁ and F₂. Since the tangent to an ellipse makes equal angles with the lines joining the point of tangency to the two foci, every trajectory through a focus will be reflected through the other focus, and so on. It is not hard to see that, irrespective of the initial direction, the trajectory after n reflections tends with increasing n to the major axis F₁F₂. If the initial ray does not go through a focus, then there are two possibilities. If it passes between the foci, then all the reflected rays will pass between the foci, and all will be tangent to a certain hyperbola having F₁ and F₂ as foci. If the initial ray does not separate F₁ and F₂, then none of the reflected rays will, and they will all be tangent to an ellipse having F₁ and F₂ as foci. Thus in no case will the motion be ergodic for the ellipse as a whole.

*Exercises: 1) Prove that if the initial ray passes through a focus of the ellipse, the nth reflection of the initial ray will tend to the major axis as n increases.

2) Prove that if the initial ray passes between the two foci, all the reflected rays will do so, and all will be tangent to some hyperbola having F₁ and F₂ as foci; similarly, if the initial ray does not pass between the foci, none of the reflected rays will, and all will be tangent to some ellipse with F₁ and F₂, as foci. (Hint: Show that the ray before and after reflection at R makes equal angles with the lines RF₁ and RF₂ respectively, and then prove that tangents to confocal conics can be characterized in this way.)