What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

*§2. THE INFINITUDE OF THE NUMBER SYSTEM. MATHEMATICAL INDUCTION

1. The Principle of Mathematical Induction

There is no end to the sequence of integers 1, 2, 3, 4, · · ·; for after any integer n has been reached we may write the next integer, n + 1. We express this property of the sequence of integers by saying that there are infinitely many integers. The sequence of integers represents the simplest and most natural example of the mathematical infinite, which plays a dominant rôle in modern mathematics. Everywhere in this book we shall have to deal with collections or “sets” containing infinitely many mathematical objects, like the set of all points on a line or the set of all triangles in a plane. The infinite sequence of integers is the simplest example of an infinite set.

The step by step procedure of passing from n to n + 1 which generates the infinite sequence of integers also forms the basis of one of the most fundamental patterns of mathematical reasoning, the principle of mathematical induction. “Empirical induction” in the natural sciences proceeds from a particular series of observations of a certain phenomenon to the statement of a general law governing all occurrences of this phenomenon. The degree of certainty with which the law is thereby established depends on the number of single observations and confirmations. This sort of inductive reasoning is often entirely convincing; the prediction that the sun will rise tomorrow in the east is as certain as anything can be, but the character of this statement is not the same as that of a theorem proved by strict logical or mathematical reasoning.

In quite a different way mathematical induction is used to establish the truth of a mathematical theorem for an infinite sequence of cases, the first, the second, the third, and so on without exception. Let us denote by A a statement that involves an arbitrary integer n. For example, A may be the statement, “The sum of the angles in a convex polygon of n + 2 sides is n times 180 degrees.” Or A′ may be the assertion, “By drawing n lines in a plane we cannot divide the plane into more than 2ⁿ parts.” To prove such a theorem for every integer n it does not suffice to prove it separately for the first 10 or 100 or even 1000 values of n. This indeed would correspond to the attitude of empirical induction. Instead, we must use a method of strictly mathematical and non-empirical reasoning whose character will be indicated by the following proofs for the special examples A and A′. In the case A, we know that for n = 1 the polygon is a triangle, and from elementary geometry the sum of the angles is known to be 1 · 180°. For a quadrilateral, n = 2, we draw a diagonal which divides the quadrilateral into two triangles. This shows immediately that the sum of the angles of the quadrilateral is equal to the sum of the angles in the two triangles, which yields 180° + 180° = 2 · 180°. Proceeding to the case of a pentagon with 5 edges, n = 3, we decompose it into a triangle plus a quadrilateral. Since the latter has the angle sum 2 · 180°, as we have just proved, and since the triangle has the angle sum 180°, we obtain 3 · 180 degrees for the 5-gon. Now it is clear that we can proceed indefinitely in the same way, proving the theorem for n = 4, then for n = 5, and so on. Each statement follows in the same way from the preceding one, so that the general theorem A can be established for all n.

Similarly we can prove the theorem A′. For n = 1 it is obviously true, since a single line divides the plane into 2 parts. Now add a second line. Each of the previous parts will be divided into two new parts, unless the new line is parallel to the first. In either case, for n = 2 we have not more than 4 = 2² parts. Now we add a third line. Each of the previous domains will either be cut into two parts or be left untouched. Thus the sum of parts is not greater than 2².2 = 2³. Knowing this to be true, we can prove the next case in the same way, and so on indefinitely.

The essential idea in the preceding arguments is to establish a general theorem A for all values of n by successively proving a sequence of special cases, A₁, A₂, · · ·. The possibility of doing this depends on two things: a) There is a general method for showing that if any statement A_r, is true then the next statement, A_r+1, will also be true. b) The first statement A₁ is known to be true. That these two conditions are sufficient to establish the truth of all the statements A₁, A₂, A₃, · · · is a logical principle which is as fundamental to mathematics as are the classical rules of Aristotelian logic. We formulate it as follows:

Let us suppose that we wish to establish a whole infinite sequence of mathematical propositions

A₁, A₂, A₃, · · ·

which together constitute the general proposition A. Suppose that a) by some mathematical argument it is shown that if r is any integer and if the assertion A_r is known to be true then the truth of the assertion A_r+1 will follow, and that b) the first proposition A₁ is known to be true. Then all the propositions of the sequence must be true, and A is proved.

We shall not hesitate to accept this, just as we accept the simple rules of ordinary logic, as a basic principle of mathematical reasoning. For we can establish the truth of every statement A_n, starting from the given assertion b) that A₁ is true, and proceeding by repeated use of the assertion a) to establish successively the truth of A₂, A₃, A₄, and so on until we reach the statement A_n. The principle of mathematical induction thus rests on the fact that after any integer r there is a next, r + 1, and that any desired integer n may be reached by a finite number of such steps, starting from the integer 1.

Often the principle of mathematical induction is applied without explicit mention, or is simply indicated by a casual “etc.” or “and so on.” This is especially frequent in elementary instruction. But the explicit use of an inductive argument is indispensable in more subtle proofs. We shall give a few illustrations of a simple but not quite trivial character.

2. The Arithmetical Progression

For every value of n, the sum 1 + 2 + 3 + · · · + n of the first n integers is equal to . In order to prove this theorem by mathematical induction we must show that for every n the assertion A_n:

(1)   

is true. a) We observe that if r is an integer and if the statement A_r, is known to be true, i.e. if it is known that

then by adding the number (r + 1) to both sides of this equation we obtain the equation

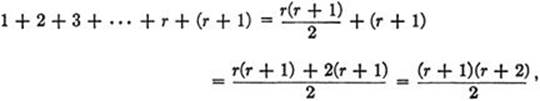
which is precisely the statement A_r+1. b) The statement A₁ is obviously true, . Hence, by the principle of mathematical induction, the statement A_n is true for every n, as was to be proved.

Ordinarily this is shown by writing the sum 1 + 2 + 3 + · · · + n in two forms:

S_n = 1 + 2 + · · · + (n –1) + n

and

S_n = n + (n –1) + · · · + 2 + 1.

On adding, we see that each pair of numbers in the same column yields the sum n + 1, and, since there are n columns in all, it follows that

2S_n = n(n + 1),

which proves the desired result.

From (1) we may immediately derive the formula for the sum of the first (n + 1) terms of any arithmetical progression,

(2)

For

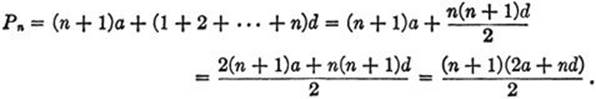
For the case a = 0, d = 1, this is equivalent to (1).

3. The Geometrical Progression

One may treat the general geometrical progression in a similar way. We shall prove that for every value of n

(3) 

(We suppose that q ≠ 1, since otherwise the right side of (3) has no meaning.)

Certainly this assertion is true for n = 1, for then it states that

And if we assume that

then we find as a consequence that

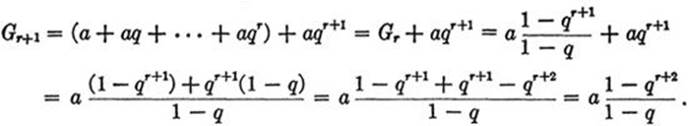
But this is precisely the assertion (3) for the case n = r + 1. This completes the proof.

In elementary textbooks the usual proof proceeds as follows. Set

G_n = a + aq + · · · + aqⁿ,

and multiply both sides of this equation by q, obtaining

qG_n = aq + aq² + · · · + aqⁿ⁺¹.

Now subtract corresponding sides of this equation from the preceding equation, obtaining

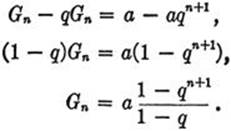
4. The Sum of the First n Squares

A further interesting application of the principle of mathematical induction refers to the sum of the first n squares. By direct trial one finds that, at least for small values of n,

(4) 

and one might guess that this remarkable formula is valid for all integers n. To prove this, we shall again use the principle of mathematical induction. We begin by observing that if the assertion A_n, which in this case is the equation (4), is true for the case n = r, so that

then on adding (r + 1)² to both sides of this equation we obtain

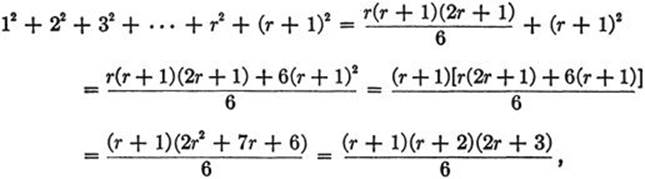
which is precisely the assertion A_r+1 in this case, since it is obtained by substituting r + 1 for n in (4). To complete the proof we need only remark that the assertion A₁, in this case the equation

is obviously true. Hence the equation (4) is true for every n.

Formulas of a similar sort may be found for higher powers of the integers, 1^k + 2^k + 3^k + · · · + n^k, where k is any positive integer As an exercise, the reader may prove by mathematical induction that

(5)  

It should be remarked that although the principle of mathematical induction suffices to prove the formula (5) once this formula has been written down, the proof gives no indication of how this formula was arrived at in the first place; why precisely the expression [n(n + 1)/2]² should be guessed as an expression for the sum of the first n cubes, rather than [n(n + 1)/3]² or (19n² – 41n + 24)/2 or any of the infinitely many expressions of a similar type that could have been considered. The fact that the proof of a theorem consists in the application of certain simple rules of logic does not dispose of the creative element in mathematics, which lies in the choice of the possibilities to be examined. The question of the origin of the hypothesis (5) belongs to a domain in which no very general rules can be given; experiment, analogy, and constructive intuition play their part here. But once the correct hypothesis is formulated, the principle of mathematical induction is often sufficient to provide the proof. Inasmuch as such a proof does not give a clue to the act of discovery, it might more fittingly be called a verification.

*5. An Important Inequality

In a subsequent chapter we shall find use for the inequality

(6) (1 + p)ⁿ ≥ 1 + np,

which holds for every number p > –1 and positive integer n. (For the sake of generality we are anticipating here the use of negative and non-integral numbers by allowing p to be any number greater than –1. The proof for the general case is exactly the same as in the case where p is a positive integer.) Again we use mathematical induction.

a) If it is true that (1 + p)^r ≥ 1 + rp, then on multiplying both sides of this inequality by the positive number 1 + p, we obtain

(1 + p)^r+1 ≥ 1 + rp + p + rp²

Dropping the positive term rp² only strengthens this inequality, so that

(1 + p)^r+1 ≥ 1 + (r + 1)p,

which shows that the inequality (6) will also hold for the next integer, r + 1. b) It is obviously true that (1 + p)¹ ≥ 1 + p. This completes the proof that (6) is true for every n. The restriction to numbers p > –1 is essential. If p < –1, then 1 + p is negative and the argument in a) breaks down, since if both members of an inequality are multiplied by a negative quantity, the sense of the inequality is reversed. (For example, if we multiply both sides of the inequality 3 > 2 by –1 we obtain –3 > –2, which is false.)

*6. The Binomial Theorem

Frequently it is important to have an explicit expression for the nth power of a binomial, (a + b)ⁿ. We find by explicit calculation that

for n = 1, (a + b)¹ = a + b,

for n = 2, (a + b)² = (a + b)(a + b) = a(a + b) + b(a + b) = a² + 2ab + b²,

for n = 3, (a + b)³ = (a + b)(a + b)² = a(a² + 2ab+ b²) + b(a² + 2ab + b²) = a³ + 3a²b + 3ab² + b³,

and so on. What general law of formation lies behind the words “and so on”? Let us examine the process by which (a + b)² was computed. Since (a + b)² = (a+ b)(a + b), we obtained the expression for (a + b)² by multiplying each term in the expression a + b by a, then by b, and adding. The same procedure was used to calculate (a + b)³ = (a + b)(a + b)². We may continue in the same way to calculate (a + b)⁴, (a + b)⁵, and so on indefinitely. The expression for (a + b)ⁿ will be obtained by multiplying each term of the previously obtained expression for (a + b)^n-1 by a, then by b, and adding. This leads to the following diagram:

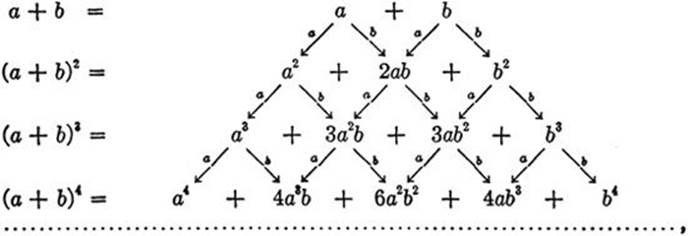
which gives at once the general rule for forming the coefficients in the expansion of (a + b)ⁿ. We construct a triangular array of numbers, starting with the coefficients 1, 1 of a + b, and such that each number of the triangle is the sum of the two numbers on each side of it in the preceding row. This array is known as Pascal’s Triangle.

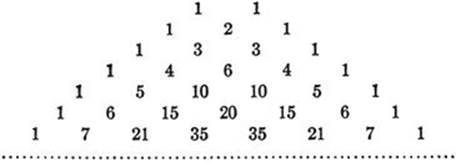
The nth row of this array gives the coefficients in the expansion of (a + b)ⁿ in descending powers of a and ascending powers of b; thus

(a + b)⁷ = a⁷ + 7a⁶b + 21a⁵b²+ 35a⁴b³+ 35a³b⁴+ 21a²b⁵+ 7ab⁶ + b⁷.

Using a concise subscript and superscript notation we may denote the numbers in the nth row of Pascal’s Triangle by

Then the general formula for. (a + b)ⁿ may be written

(7)

According to the law of formation of Pascal’s Triangle, we have

(8)    

As an exercise, the experienced reader may use this relation, together with the fact that , to show by mathematical induction that

(9)

(For any positive integer n, the symbol n! (read, “n factorial”) denotes the product of the first n integers: n! = 1·2·3 · · · n. It is convenient also to define 0! = 1, so that 9) is valid for i = 0 and i = n.) This explicit formula for the coefficients in the binomial expansion is sometimes called thebinomial theorem. (See also p. 475.)

Exercises: Prove by mathematical induction:

1)

2)

*3)

*4)

Find the sum of the following geometrical progressions:

5)

6)

7)

Using formulas (4) and (5) prove:

*8)

*9) 1³ + 3³ + ··· + (2n + 1)³ = (n + 1)²(2n² + 4n + 1)

10) Prove the same results directly by mathematical induction.

*7. Further Remarks on Mathematical Induction

The principle of mathematical induction may be generalized slightly to read: “If a sequence of statements A_s, A_s+1, A_s+2, · · · is given, where s is some positive integer, and if

a) For every value of r ≥ s, the truth of A_r+1 will follow from the truth of A_r, and

b) A_s, is known to be true,

then all the statements A_s, A_s+1, A_s+2· · · are true; that is to say, A_n is true for all n ≥ s.” Precisely the same reasoning used to establish the truth of the ordinary principle of mathematical induction applies here, with the sequence 1, 2, 3, · · · replaced by the similar sequence s, s + 1, s + 2, s + 3 · · ·. By using the principle in this form we can strengthen somewhat the inequality on page 15 by eliminating the possibility of the “=” sign. We state: For every p ≠ 0 and > –1 and every integer n ≥ 2,

(10)    (1 + p)ⁿ > 1 + np.

The proof will be left to the reader.

Closely related to the principle of mathematical induction is the “principle of the smallest integer” which states that every non-empty set C of positive integers has a smallest member. A set is empty if it has no members, e.g., the set of straight circles or the set of integers n such that n > n. For obvious reasons we exclude such sets in the statement of the principle. The set C may be finite, like the set 1, 2, 3, 4, 5, or infinite, like the set of all even numbers 2, 4, 6, 8, 10, · · ·. Any non-empty set C must contain at least one integer, say n, and the smallest of the integers 1, 2, 3, · · ·,n that belongs to C will be the smallest integer in C.

The only way to realize the significance of this principle is to observe that it does not apply to every set C of numbers that are not integers; for example, the set of positive fractions does not contain a smallest member.

From the point of view of logic it is interesting to observe that the principle of the smallest integer may be used to prove the principle of mathematical induction as a theorem. To this end, let us consider any sequence of statements A₁, A₂, A₃, · · · such that

a) For any positive integer r the truth of A_r+1 will follow from that of A_r.

b) A₁ is known to be true.

We shall show the hypothesis that any one of the A′s is false to be untenable. For if even one of the A′s were false, the set C of all positive integers n for which A_n is false would be non-empty. By the principle of the smallest integer, C would contain a smallest integer, p, which must be > 1 because of b). Hence A_p would be false, but A_p-1 true. This contradicts a)..

Once more we emphasize that the principle of mathematical induction is quite distinct from empirical induction in the natural sciences. The confirmation of a general law in any finite number of cases, no matter how large, cannot provide a proof for the law in the rigorous mathematical sense of the word, even if no exception is known at the time. Such a law would remain only a very reasonable hypothesis, subject to modification by the results of future experience. In mathematics, a law or a theorem is proved only if it can be shown to be a necessary logical consequence of certain assumptions which are accepted as valid. There are many examples of mathematical statements which have been verified in every particular case considered thus far, but which have not yet been proved to hold in general (for an example see p. 30). One may suspect that a theorem is true in all generality by observing its truth in a number of examples; one may then attempt to prove it by mathematical induction. If the attempt succeeds the theorem is proved to be true; if the attempt fails, the theorem may be true or false and may some day be proved or disproved by other methods.

In using the principle of mathematical induction one must always be sure that the conditions a) and b) are really satisfied. Neglect of this precaution may lead to absurdities like the following, in which the reader is invited to discover the fallacy. We shall “prove” that any two positive integers are equal; for example, that 5 = 10.

First a definition: If a and b are two unequal positive integers, we define max (a, b) to be a or b, whichever is greater; if a = b we set max (a, b) = a = b. Thus max (3, 5) = max (5, 3) = 5, while max (4, 4) = 4. Now let A_n be the statement, “If a and b are any two positive integers such that max (a, b) = n, then a = b.”

a) Suppose A_r to be true. Let a and b be any two positive integers such that max (a, b) = r + 1. Consider the two integers

α = a – 1

β = b – 1;

then max (α, β) = r. Hence α = β, for we are assuming A_r to be true. It follows that a = b; hence A_r+1 is true.

b) A₁ is obviously true, for if max (a, b) = 1, then since a and b are by hypothesis positive integers they must both be equal to 1. Therefore, by mathematical induction, A_n is true for every n.

Now if a and b are any two positive integers whatsoever, denote max (a, b) by r. Since A_n has been shown to be true for every n, in particular A_r is true. Hence a = b.