What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

§8. THE ISOPERIMETRIC PROBLEM

That the circle encloses the largest area among all closed curves with a prescribed length is one of the “obvious” facts of mathematics for which only modern methods have yielded a rigorous proof. Steiner devised various ingenious ways of proving this theorem, of which we shall consider one.

Let us start with the assumption that a solution does exist. This granted, suppose the curve C is the required one with the prescribed length L and maximum area. Then we can easily show that C must be convex, in the sense that the straight segment joining any two points of C must lie entirely inside or on C. For if C were not convex, as in Figure 226, then a segment such as OP could be drawn between some pair of points O and P on C, such that OP lies outside of C. The arc OQ′P which is the reflection of OQP in the line OP forms, together with the arc ORP, a curve of length L enclosing a larger area than the original curve C, since it includes the additional areas I and II. This contradicts the assumption that C contains the largest area for a closed curve of length L. Hence C must be convex.

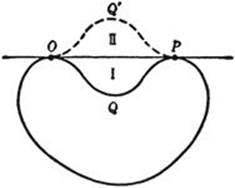
Fig. 226

Now choose two points, A, B, dividing the solution curve C into arcs of equal length. Then the line AB must divide the area of C into two equal parts, for otherwise the part of greater area could be reflected in AB (Fig. 227) to give another curve of length L with greater included area thatC. It follows that half of the solution C must solve the following problem: To find the arc of length L/2 having its endpoints A, B on a straight line and enclosing a maximum area between it and this straight line. Now we shall show that the solution to this new problem is a semicircle, so that the whole curve C solving the isoperimetric problem is a circle. Let the arc AOB solve the new problem. It is sufficient to show that every inscribed angle such as AOB in Figure 228 is a right angle, for this will prove that AOB is a semicircle. Suppose, on the contrary, that the angle AOBis not 90°. Then we can replace Figure 228 by another one, 229, in which the shaded areas and the length of the arc AOB are not changed, while the triangular area is increased by making AOB equal to or at least nearer to 90°. Thus Figure 229 gives a larger area than the original (see page 330). But we started with the assumption that Figure 228 solves the problem so that Figure 229 could not possibly yield a larger area. This contradiction shows that for every point O, AOB must be a right angle, and this completes the proof.

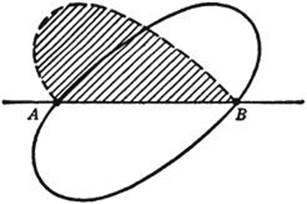
Fig. 227

The isoperimetric property of the circle can be expressed in the form of an inequality. If L is the circumference of the circle, its area is L²/4π, and therefore we must have the isoperimetric inequality, A ≤ L²/4π, between the area A and length L of any closed curve the equality sign holding only for the circle.

*As is apparent from the discussion in §7, Steiner’s proof has only a conditional value: “If there is a curve of length L within maximal area then it must be a circle.” To establish the hypothetical premise an essentially new argument is needed. First we prove an elementary theorem concerning closed polygons P_n with an even number 2n of edges: Among all such 2n-gons with the same length, the regular 2n-gon has the largest area. The proof follows the pattern of Steiner’s reasoning with the following modifications. There is no difficulty about the question of existence here, since a 2n-gon, together with its length and area, depends continuously on the 4n coördinates of its vertices, which may without loss of generality be restricted to a compact set of points in 4n-dimentional space. Accordingly, in this problem for polygons we may safely begin with the assumption that some polygon P is the solution, and on this basis analyze the properties of P. Exactly as in Steiner’s proof, it follows that P must be convex. We prove now that all the 2n edges of P must have the same length. For assume that two adjacent edges AB and BC had different lengths; then we could cut off triangle ABC from P and replace it by an isosceles triangle AB′C, in which AB′ + B′C = AB + BC, and which has a larger area (see §1). Thus we would obtain a polygon P′ with the same perimeter and a larger area, contrary to the assumption that P was the optimal polygon of 2n edges. Therefore all the edges of P must have equal length, and what remains to be shown is that P is regular; for this it suffices to know that all the vertices of P lie on a circle. The reasoning follows Steiner’s pattern. First we show that any diagonal joining opposite vertices, e.g. the first with the (n + 1)-st, cuts the area in two equal parts. Then we prove that all the vertices of one of these parts lie on a semicircle. The details, which follow exactly the previous pattern, are left to the reader as an exercise.

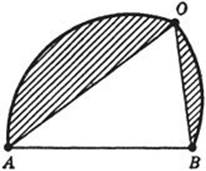
Fig. 228

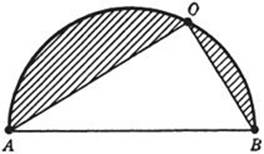
Fig. 229

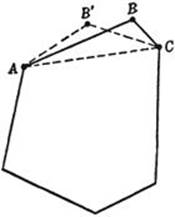
Fig. 230

The existence, together with the solution, of the isoperimetric problem can now be obtained by a limiting process in which the number of vertices tends to infinity and the optimal regular polygon to a circle.

Steiner’s reasoning is not at all suited to proving the corresponding isoperimetric property of the sphere in three dimensions. A somewhat different and more complicated treatment was given by Steiner that works for three dimensions as well as for two, but since it cannot be so immediately adapted to giving the existence proof it is omitted here. As a matter of fact, proving the isoperimetric property of the sphere is a much harder task than for the circle; indeed, a complete and rigorous proof was first given much later, in a rather difficult paper by H. A. Schwarz. The three-dimensional isoperimetric property can be expressed by the inequality

36πV² ≤ A³

between the surface area A and the volume V of any closed three-dimensional body, the equality holding only for the sphere.