What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

§11. EXPERIMENTAL SOLUTIONS OF MINIMUM PROBLEMS. SOAP FILM EXPERIMENTS

1. Introduction

It is usually very difficult, and sometimes impossible, to solve variational problems explicitly in terms of formulas or geometrical construetions involving known simple elements. Instead, one is often satisfied with merely proving the existence of a solution under certain conditions and afterwards investigating properties of the solution. In many cases, when such an existence proof turns out to be more or less difficult, it is stimulating to realize the mathematical conditions of the problem by corresponding physical devices, or rather, to consider the mathematical problem as an interpretation of a physical phenomenon. The existence of the physical phenomenon then represents the solution of the mathematical problem. Of course, this is only a plausibility consideration and not a mathematical proof, since the question still remains whether the mathematical interpretation of the physical event is adequate in a strict sense, or whether it gives only an inadequate image of physical reality. Sometimes such experiments, even if performed only in the imagination, are convincing even to mathematicians. In the nineteenth century many of the fundamental theorems of function theory were discovered by Riemann by thinking of simple experiments concerning the flow of electricity in thin metallic sheets.

In this section we wish to discuss, on the basis of experimental demonstrations, one of the deeper problems of the calculus of variations. This problem has been called Plateau’s problem, because Plateau (1801–1883), a Belgian physicist, made interesting experiments on this subject. The problem itself is much older and goes back to the initial phases of the calculus of variations. In its simplest form it is the following: to find the surface of smallest area bounded by a given closed contour in space. We shall also discuss experiments connected with some related questions, and it will turn out that much light can thus be thrown on some of our previous results as well as on certain mathematical problems of a new type.

2. Soap Film Experiments

Mathematically, Plateau’s problem is connected with the solution of a “partial differential equation,” or a system of such equations. Euler showed that all (non-plane) minimal surfaces must be saddle-shaped and that the mean curvature† at every point must be zero. The solution was shown to exist for many special cases during the last century, but the existence of the solution for the general case was proved only recently, by J. Douglas and by T. Radò.

Plateau’s experiments immediately yield physical solutions for very general contours. If one dips any closed contour made of wire into a liquid of low surface tension and then withdraws it, a film in the form of a minimal surface of least area will span the contour. (We assume that we may neglect gravity and other forces which interfere with the tendency of the film to assume a position of stable equilibrium by attaining the smallest possible area and thus the least possible value of the potential energy due to surface tension.) A good recipe for such a liquid is the following: Dissolve 10 grams of pure dry sodium oleate in 500 grams of distilled water, and mix 15 cubic units of the solution with 11 cubic units of glycerin. Films obtained with this solution and with frames of brass wire are relatively stable. The frames should not exceed five or six inches in diameter.

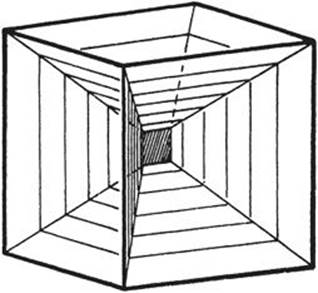
Fig. 240. Cubic frame spanning a soap film system of 13 nearly plane surfaces.

With this method it is very easy to “solve” Plateau’s problem simply by shaping the wire into the desired form. Beautiful models are obtained in polygonal wire frames formed by a sequence of edges of a regular polyhedron. In particular, it is interesting to dip the whole frame of a cube into such a solution. The result is first a system of different surfaces meeting each other at angles of 120° along lines of intersection. (If the cube is withdrawn carefully, there will be thirteen nearly plane surfaces.) Then we may pierce and destroy enough of these different surfaces so that only one surface bounded by a closed polygon remains. Several beautiful surfaces may be formed in this way. The same experiment can also be performed with a tetrahedron.

3. New Experiments on Plateau’s Problem

The scope of soap film experiments with minimal surfaces is wider than these original demonstrations by Plateau. In recent years the problem of minimal surfaces has been studied when not only one but any number of contours is prescribed, and when, in addition, the topological structure of the surface is more complicated. For example, the surface might be one-sided or of genus different from zero. These more general problems produce an amazing variety of geometrical phenomena that can be exhibited by soap film experiments. In this connection it is very useful to make the wire frames flexible, and to study the effect of deformations of the prescribed boundaries on the solution.

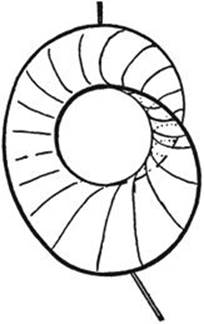
Fig. 241. One-sided surface (Moebius strip).

Fig. 242. Two-sided surface.

We shall describe several examples:

1) If the contour is a circle we obtain a plane circular disk. If we continuously deform the boundary circle we might expect that the minimal surface would always retain the topological character of a disk. This is not the case. If the boundary is deformed into the shape indicated by Figure 241, we obtain a minimal surface that is no longer simply connected, like the disk, but is a one-sided Moebius strip. Conversely, we might start with this frame and with a soap film in the shape of a Moebius strip. We may deform the wire frame by pulling handles soldered to it (Fig. 241). In this process we shall reach a moment when suddenly the topological character of the film changes, so that the surface is again of the type of a simply connected disk (Fig. 242). Reversing the deformation we again obtain a Moebius strip. In this alternating deformation process the mutation of the simply connected surface into the Moebius strip takes place at a later stage. This shows that there must be a range of shapes of the contour for which both the Moebius strip and the simply connected surface are stable, i.e. furnish relative minima. But when the Moebius strip has a much smaller area than the other surface, the latter is too unstable to be formed.

2) We may span a minimal surface of revolution between two circles. After the withdrawal of the wire frames from the solution we find, not one simple surface, but a structure of three surfaces meeting at angles of 120°, one of which is a simple circular disk parallel to the prescribed boundary circles (Figure 243). By destroying this intermediate surface the classical catenoid is produced (the catenoid is the surface obtained by revolving the catenary of page 382 about a line perpendicular to its axis of symmetry). If the two boundary circles are pulled apart, there is a moment when the doubly connected minimal surface (the catenoid) becomes unstable. At this moment the catenoid jumps discontinuously into two separated disks. This process is, of course, not reversible.

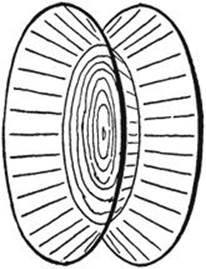
Fig. 243. System of three surfaces

3) Another significant example is provided by the frame of Figures 244–6 in which can be spanned three different minimal surfaces. Each is bounded by the same simple closed curve; one (Figure 244) has the genus 1, while the other two are simply connected, and in a way symmetrical to each other. The latter have the same area if the contour is completely symmetrical. But if this is not the case then only one gives the absolute minimum of the area while the other will give a relative minimum, provided that the minimum is sought among simply connected surfaces. The possibility of the solution of genus 1 depends on the fact that by admitting surfaces of genus 1 one may obtain a smaller area than by requiring that the surface be simply connected. By deforming the frame we must, if the deformation is radical enough, come to a point where this is no longer true. At that moment the surface of genus 1 becomes more and more unstable and suddenly jumps discontinuously into the simply connected stable solution represented by Figure 245 or 246. If we start with one of these simply connected solutions, such as Figure 246, we may deform it in such a way that the other simply connected solution of Figure 245 becomes much more stable. The consequence is that at a certain moment a discontinuous transition from one to the other will take place. By slowly reversing the deformation, we return to the initial position of the frame, but now with the other solution in it. We can repeat the process in the opposite direction, and in this way swing back and forth by discontinuous transitions between the two types. By careful handling, one may also transform discontinuously either one of the simply connected solutions into that of genus 1. For this purpose we have to bring the disk-like parts very close to each other, so that the surface of genus 1 becomes markedly more stable. Sometimes in this process intermediate pieces of film appear first and have to be destroyed before the surface of genus 1 is obtained.

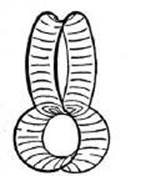
Fig. 244.

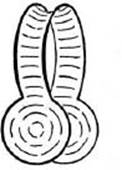
Fig. 245.

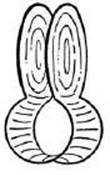
Fig. 246.

Frame spanning three different surfaces of genus 0 and 1.

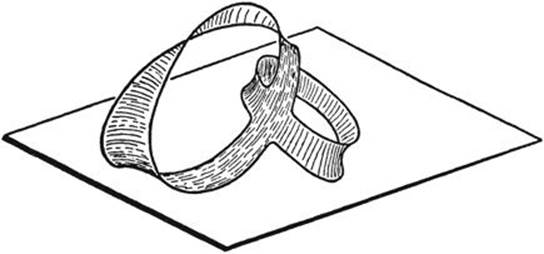
Fig. 247. One-sided minimal surface of higher topological structure in a single contour.

This example shows not only the possibility of different solutions of the same topological type, but also of another and different type in one and the same frame; moreover, it again illustrates the possibility of discontinuous transitions from one solution to another while the conditions of the problem are changed continuously. It is easy to construct more complicated models of the same sort and to study their behavior experimentally.

An interesting phenomenon is the appearance of minimal surfaces bounded by two or more interlocked closed curves. For two circles we obtain the surface shown in Figure 248. If, in this example, the circles are perpendicular to each other and the line of intersection of their planes is a diameter of both circles, there will be two symmetrically opposite forms of this surface with equal area. If the circles are now moved slightly with respect to each other, the form will be altered continuously, although for each position only one form is an absolute minimum, and the other one a relative minimum. If the circles are moved so that the relative minimum is formed, it will jump over into the absolute minimum at some point. Here both of the possible minimal surfaces have the same topological character, as do the surfaces of Figures 245–6 one of which can be made to jump into the other by a slight deformation of the frame.

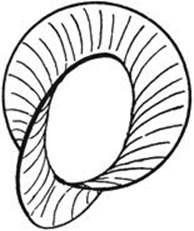
Fig. 248. Interlocked curves.

4. Experimental Solutions of Other Mathematical Problems

Owing to the action of surface tension, a film of liquid is in stable equilibrium only if its area is a minimum. This is an inexhaustible source of mathematically significant experiments. If parts of the boundary of a film are left free to move on given surfaces such as planes, then on these boundaries the film will be perpendicular to the prescribed surface.

We can use this fact for striking demonstrations of Steiner’s problem and its generalizations (see §5). Two parallel glass or transparent plastic plates are joined by three or more perpendicular bars. If we immerse this object in a soap solution and withdraw it, the film forms a system of vertical planes between the plates and joining the fixed bars. The projection appearing on the glass plates is the solution of the problem discussed on page 359.

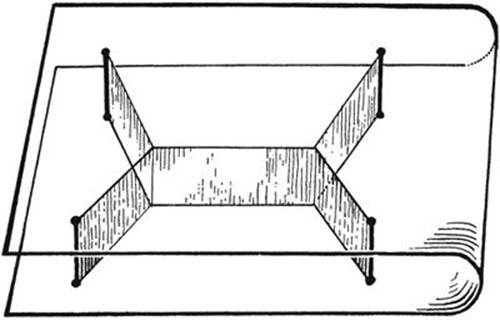
Fig. 249. Demonstration of the shortest connection between 4 points.

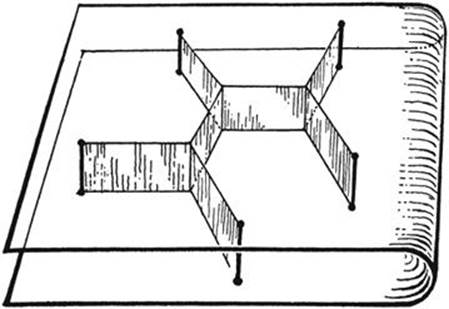
Fig. 250. Shortest connection between 5 points.

If the plates are not parallel, the bars not perpendicular to them, or the plates curved, then the curves formed by the film on the plates will not be straight, but will illustrate new variational problems.

The appearance of lines where three sheets of a minimal surface meet at angles of 120° may be regarded as the generalization to more dimensions of the phenomena connected with Steiner’s problem. This becomes clear e.g. if we join two points A, B in space by three curves, and study the corresponding stable system of soap films. As the simplest case we take for one curve the straight segment AB, and for the

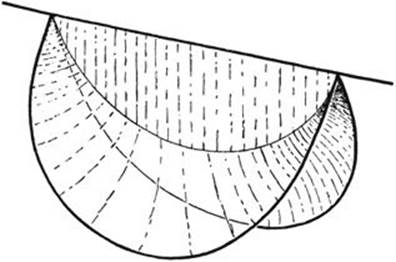
Fig. 251. Three surfaces meeting at 120° spanned between three wires joining two points. others two congruent circular arcs. The result is shown in Figure 251. If the planes of the arcs form an angle of less than 120°, we obtain three surfaces meeting at angles of 120°; if we turn the two arcs, increasing the included angle, the solution changes continuously into two plane circular segments.

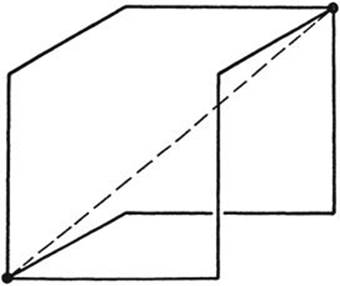
Fig. 252. Three broken lines joining two points.

Now let us join A and B by three more complicated curves. As an example we may take three broken lines each consisting of three edges of the same cube that join two diagonally opposite vertices: we obtain three congruent surfaces meeting in the diagonal of the cube. (We obtain this system of surfaces from that depicted in Fig. 240 by destroying the films adjacent to three properly selected edges.) If we make the three broken lines joining A and B movable, we can see the line of threefold intersection become curved. The angles of 120° will be preserved (Fig. 252).

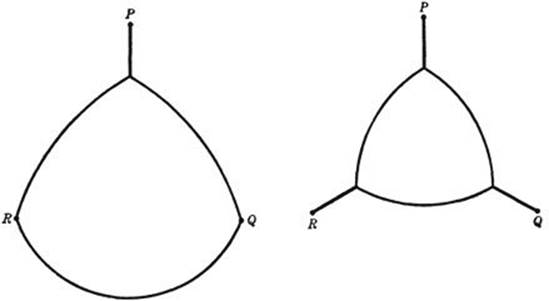
All the phenomena where three minimal surfaces meet in certain lines are fundamentally of a similar nature. They are generalizations of the plane problem of joining n points by the shortest system of lines.

Fig. 253. Demonstration that the circle has least perimeter for a given area.

Finally, a word about soap bubbles. The spherical soap bubble shows that among all closed surfaces including a given volume (defined by the amount of air inside), the sphere has the least area. If we consider soap bubbles of given volume which tend to contract to a minimum area but which are restricted by certain conditions, then the resulting surfaces will be not spheres, but surfaces of constant mean curvature, of which spheres and circular cylinders are special examples.

For example, we blow a soap bubble between two parallel glass plates which have previously been wetted by the soap solution. When the bubble touches one plate, it suddenly assumes the shape of a hemisphere; as soon as it also touches the other plate, it jumps into the shape of a circular cylinder, thus demonstrating the isoperimetric property of the circle in a most striking way. The fact that the soap film adjusts itself vertically to the bounding surface is the key to this experiment. By blowing soap bubbles between two plates with perpendicular connecting rods, we can illustrate the problems discussed on pp. 378–9.

We can study the behavior of the solution of the isoperimetric problem by increasing or decreasing the amount of air in the bubble, using a tube with a fine point. By sucking out air, however, we do not obtain the figures of page 378 consisting of circular arcs tangent to each other. As the volume of air included decreases, the angles of the circular triangle will (theoretically) not decrease below 120°; we obtain the shapes shown in Figures 254–5, which again tend to straight segments as in Figure 235 as the area tends to zero. The mathematical reason for the failure of soap films to form tangent arcs is the fact that as soon as the bubble separates from the vertices, the connecting lines must no longer be counted twice. The corresponding experiments are illustrated by Figures 256 and 257.

Figs. 254–5. Isoperimetric figures with boundary restrictions.

* Exercise: Study the corresponding mathematical problem: a circular triangle is to be found including a given area and such that its perimeter plus three segments joining the vertices to the given points has a minimum length.

A cubic frame inside of which we blow a bubble will provide surfaces of constant mean curvature with a quadratic base, if the bubble bulges out of the frame. As we remove air from the bubble by sucking through a straw, we obtain a sequence of beautiful structures which result in that ofFigure 258. The phenomena of stability and transition between different states of equilibria are a source of experiments that are very illuminating from the mathematical point of view. The experiments illustrate the theory of stationary values, since the transitions can be made to take place so as to lead through an unstable equilibrium which is a “stationary state.”

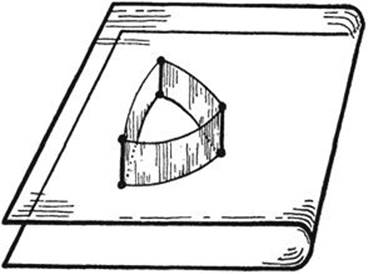
FIG. 256

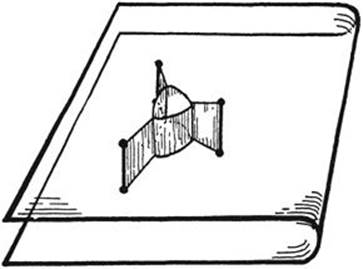
FIG. 257

For example, the cubical structure of Figure 240 exhibits asymmetry insofar as a vertical plane in the center connects the twelve surfaces issuing from the edges. Hence there must be at least two other positions of equilibrium, one with a vertical and one with a horizontal central square. As a matter of fact, by blowing through a fine tube against the edges of this square, one can force the structure into a position where the square reduces to a point, the center of the cube; this position of unstable equilibrium will immediately go into one of the other stable positions obtained from the original by a rotation through 90°.

A similar experiment can be performed on the soap film that demonstrates Steiner’s problem for four points forming a square (Figs. 219–20).

If we want to obtain the solutions of such problems as limiting cases of isoperimetric problems—for example, if we want to obtain Figure 240 from Figure 258—we must suck the air out of the bubble. Now Figure 258 is completely symmetric, and its limit for vanishing content of the bubble would be a symmetric system of 12 planes meeting at the center. This can really be observed. But the position obtained as a limit is not in stable equilibrium; instead, it will change over into one of the positions of Figure 240. By using a somewhat more viscous liquid than that described above the whole phenomenon can be observed very easily. It exemplifies the fact that even in physical problems the solution of a problem need not depend continuously on the data; for in the limiting case for volume zero the solution, given by Figure 240, is not the limit of the solution, given by Figure 258, for volume ε as ε tends to zero.

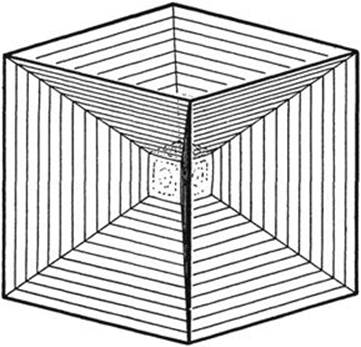
Fig. 258.