What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

§3. THE TECHNIQUE OF DIFFERENTIATION

Until now our efforts have been devoted to differentiating a variety of specific functions by transforming the difference quotients in preparation for passage to the limit. It was a decisive step when, through the work of Leibniz, Newton, and their successors, these individual devices were replaced by powerful general methods. By these methods one can differentiate almost automatically any function that normally occurs in mathematics, provided one has mastered a few simple rules and can recognize their applicability. Thus differentiation has acquired the character of an “algorithm” of calculation, and it is this aspect of the theory that is expressed by the term “calculus.”

We cannot go far into the details of this technique. Only a few simple rules will be mentioned.

(a) Differentiation of a sum. If a and b are constants and the function k(x) is given by

k(x) = af(x) + bg(x),

then, as the reader can easily verify,

k′(x) = af′(x) + bg′(x).

A similar rule holds for any number of terms.
(b) Differentiation of a product. For a product,

p(x) = f(x)g(x),

the derivative is

p′(x) = f(x)g′(x) + g(x)f′(x).

This is easily proved by the following device: we write, adding and subtracting the same term,

p(x + h) – p(x) = f(x + h)g(x + h) – f(x)g(x)

= f(x + h)g(x + h) – f(x + h)g(x) + f(x + h)g(x) – f(x)g(x),

and obtain, by combining the first two and the second two terms,

Now we let h approach zero; since f(x + h) approaches f(x), the statement to be proved follows immediately.

Exercise: Prove that the function p(x) = xⁿ has the derivative p′(x) = nx^n–1.

(Hint: Write xⁿ = x·x^n–1 and use mathematical induction.)

Using rules (a) and (b) we can differentiate any polynomial

f(x) = a₀ + a₁x + · · · + a_nxⁿ;

the derivative is

f′(x) = a₁ + 2a₂x + 3a₃x² + · · · + na_nx^n–1.

As an application we may prove the binomial theorem (compare p. 17. This theorem concerns the expansion of (1 + x)ⁿ as a polynomial:

(1) J(x) = (1 + x)ⁿ = 1 + a₁x + a₂x² + a₃x³ + · · · + a_nxⁿ, and states that the coefficient a_k is given by the formula

(2) 

Of course, a_n = 1.

We have seen (Exercise, p. 421) that the left side of (1) differentiated yields n(1 + x)^n–1. Thus by the preceding paragraph we obtain

(3) n(1 + x)^n–1 = a₁ + 2a₂x + 3a₃x² + · · · + na_nx^n–1.

In this formula we now set x = 0 and find that n = a₁, which is (2) for k = 1. Then we differentiate (3) again, obtaining

n(n – 1)(1 + x)^n-2 = 2a₂ + 3·2a₃x +... + n(n – 1)a_nx^n–2.

Substituting x = 0, we find n(n – 1) = 2a₂ in agreement with (2) for k= 2.

Exercise: Prove (2) for k = 3, 4, and for general k by mathematical induction

(c) Differentiation of a quotient. If

then

The proof is left as an exercise. (Of course, we must assume g(x) ≠ 0.)

Exercise: Derive by this rule the formulas of page 422 for the derivatives of tan x and cot x from those for sin x and cos x. Prove that the derivatives of sec x = 1/cos x and cosec x = 1/sin x are sin x/cos² x and –cos x/sin² x respectively.

We are now able to differentiate any function that can be written as the quotient of two polynomials. For example,

has the derivative

Exercise: Differentiate

where m is a positive integer. The result is

f′(x) = –mx^–m–1,

(d) Differentiation of inverse functions. If

y = f(x) and x = g(y)

are inverse functions (e.g. y = x² and ), then their derivatives are reciprocal:

This fact is easily proved by going back to the reciprocal difference quotients and respectively; it can also be seen from the geometrical interpretation of the inverse function given on page 281, if we refer the slope of the tangent to the y-axis instead of to the x-axis.

As an example we differentiate the function

inverse to x = y^m. (See also the more direct treatment for m = on p. 421.) Since the latter function has as its derivative the expression my^m–1, we have

whence, after substituting and y^–m = x^–1, , or

.

As a further example we differentiate the inverse trigonometric function (see page 281):

y = arc tan x, which means the same as x = tan y.

Here the variable y, denoting the radian measure, is restricted to the interval so as to insure a unique definition of the inverse function.

Since we have (see page 422) D tan y = 1/cos² y and since 1/cos² y = (sin² y + cos² y)/cos² y = 1 + tan² y = 1 + x², we find:

In the same way the reader may derive the following formulas:

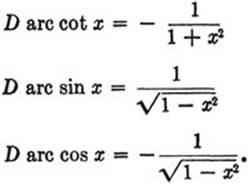
Finally, we come to the important rule for

(e) Differentiation of compound functions. Such functions are compounded from two (or more) simpler ones (see p. 282). For example, is compounded from z = sin y and y and ; the function is compounded from z = y + y⁵ and ; z =

Fig. 272

Fig. 273

sin (x²) is a compound of z = sin y and y = x²; is a compound of z = sin y and

If two functions

z = g(y) and y = f(x)

are given, and if the latter function is substituted in the former, we obtain the compound function

z = k(x) = g[f(x)].

We assert that

(4)  k′(x) = g′(y)f′(x).

For if we write

where y = f(x₁) and z₁ = g(y₁) = k(x₁), and then let x₁ approach x, the left side approaches k′(x) and the two factors on the right hand side approach g′(y) and f′(x) respectively, thus proving (4).

In this proof the condition y₁ – y ≠ 0 was necessary. For we divided by Δy = y₁ – y, and we cannot use values x₁ for which y₁ – y = 0. But the formula (4) remains valid even if Δy = 0 in an interval around x; y is then constant, f′(x) = 0, k(x) = g(y) is constant with respect to x (since y does not change with x), and hence k′(x) = 0, as (4) states in this case.

The reader should verify the following examples:

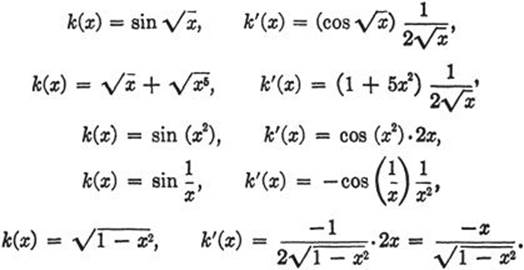
Exercise: Combining the results of pages 420 and 430, show that the function

has the derivative

It should be noted that all our formulas concerning powers of x can now be combined into a single one:

If r is any positive or negative rational number, then the function

f(x) = x^r.

has the derivative

f′(x) = rx^r–1.

Exercises: 1) Carry out the differentiations of the exercises on page 421 by using the rules of this section.

2) Differentiate the following functions: x sin x,, (x³ – 3x² – x + 1)³, 1 + sin² x arc sin (cos nx),

3) Find the second derivatives of some of the preceding functions and of , arc tan x, sin² x, tan x.

4) Differentiate *and prove the minimum properties of the light ray by reflection and by refraction stated in Chapter VII, pp. 330 and 382. The reflection or refraction is to be in the x-axis, and the coördinates of the endpoints of the path may bex₁, y₁ and x₂, y₂ respectively.

(Remark: The function possesses only one point with vanishing derivative; therefore, since a minimum but obviously no maximum occurs, there is no need to study the second derivative.)

More Problems on Maxima and Minima: 5) Find the extrema of the following functions, sketch their graphs, determine the intervals of increase, decrease, convexity, and concavity:

x³ – 6x + 2, x/(1 + x²), x²/(1 + x⁴), cos² x.

6) Study the maxima and minima of the function x²+ 3ax + 1 in their dependence on a.

7) Which point of the hyperbola 2y² – x² = 2 is nearest to the point x = 0, y = 3?

8) Of all rectangles with given area find the one with the shortest diagonal.

9) Inscribe the rectangle of greatest area in the ellipse x²/a² + y²/b² = 1.

10) Of all circular cylinders with given volume find the one with the leastarea.