What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

§2. CONGRUENCES

1. General Concepts

Whenever the question of the divisibility of integers by a fixed integer d occurs, the concept and the notation of “congruence” (due to Gauss) serves to clarify and simplify the reasoning.

To introduce this concept let us examine the remainders left when integers are divided by the number 5. We have

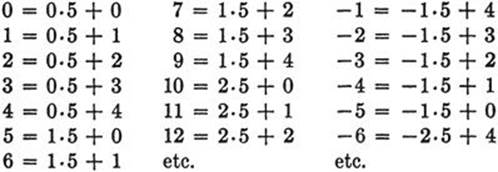
We observe that the remainder left when any integer is divided by 5 is one of the five integers 0, 1, 2, 3, 4. We say that two integers a and b are “congruent modulo 5” if they leave the same remainder on division by 5. Thus 2, 7, 12, 17, 22, · · ·, –3, –8, –13, –18, ··· are all congruent modulo 5, since they leave the remainder 2. In general, we say that two integers a and b are congruent modulo d, where d is a fixed integer, if a and b leave the same remainder on division by d, i.e., if there is an integer n such that a – b = nd. For example, 27 and 15 are congruent modulo 4, since

27 = 6·4 + 3, 15 = 3·4 + 3.

The concept of congruence is so useful that it is desirable to have a brief notation for it. We write

a ≡ b (mod d)

to express the fact that a and b are congruent modulo d. If there is no doubt concerning the modulus, the “mod d” of the formula may be omitted. (If a is not congruent to b modulo d, we shall write a b (mod d).)

Congruences occur frequently in daily life. For example, the hands on a clock indicate the hour modulo 12, and the mileage indicator on a car gives the total miles traveled modulo 100,000.

Before proceeding with the detailed discussion of congruences the reader should observe that the following statements are all equivalent:

1. a is congruent to b modulo d.

2. a = b + nd for some integer n.

3. d divides a – b.

The usefulness of Gauss’s congruence notation lies in the fact that congruence with respect to a fixed modulus has many of the formal properties of ordinary equality. The most important formal properties of the relation a = b are the following:

1) Always a = a.

2) If a = b, then b = a.

3) If a = b and b = c, then a= c.

Moreover, if a = a′ and b = b′, then

4) a + b = a′ + b′.

5) a – b = a′ – b′.

6) ab = a′b′.

These properties remain true when the relation a = b is replaced by the congruence relation a ≡ b (mod d). Thus

1′) Always a ≡ a (mod d).

2′) If a ≡ b (mod d) then b ≡ a (mod d).

3′) If a ≡ b (mod d) and b≡ c (mod d), then a ≡ c (mod d).

The trivial verification of these facts is left to the reader.

Moreover, if a ≡ a′ (mod d) and b ≡ b′ (mod d), then

4′) a + b≡ a′ + b′ (mod d).

5′) a – b≡ a′ – b′ (mod d).

6′) ab ≡ a′ b′ (mod d).

Thus congruences with respect to the same modulus may be added, subtracted, and multiplied. To prove these three statements we need only observe that if

a = a′ + rd, b = b′+ sd,

then

a + b = a′ + b′ + (r + s)d,

a – b = a′ – b′ + (r – s)d,

ab = a′b′ + (a′s + b′r + rsd)d,

from which the desired conclusions follow.

The concept of congruence has an illuminating geometrical interpretation. Usually, if we wish to represent the integers geometrically, we choose a segment of unit length and extend it by multiples of its own length in both directions. In this way we can find a point on the line corresponding to each integer, as in Figure 6. But when we are dealing with the integers modulo d, any two congruent numbers are considered the same as far as their behavior on division by a is concerned, since they leave the same remainder. In order to show this geometrically, we use a circle divided into d equal parts. Any integer when divided by d leaves as remainder one of the d numbers 0, 1, ···, d – 1, which are placed at equal intervals on the circumference of the circle. Every integer is congruent modulo d to one of these numbers, and hence is represented geometrically by one of these points; two numbers are congruent if they are represented by the same point. Figure 7 is drawn for the case d = 6. The face of a clock is another illustration from daily life.

Fig. 6. Geometrical representation of the integers.

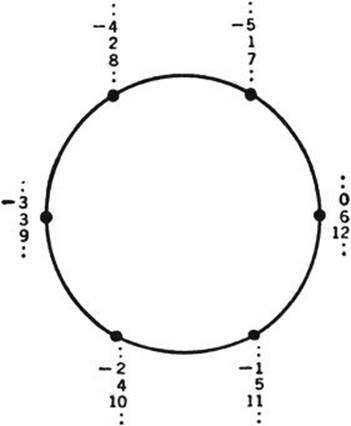
Fig. 7. Geometrical representation of the integers modulo 6.

As an example of the use of the multiplicative property 6’) of congruences we may determine the remainders left when successive powers of 10 are divided by a given number. For example,

10 ≡ –1    (mod 11),

since 10 = –1 + 11. Successively multiplying this congruence by itself, we obtain

From this we can show that any integer

z = a₀ + a₁·10 + a₂·10² + · · · + an·10ⁿ,

expressed in the decimal system, leaves the same remainder on division by 11 as does the sum of its digits, taken with alternating signs,

t = a_o– a₁ + a₂ – a₃ + · · ·.

For we may write

z – t = a₁·11 + a₂ (10² – 1) + a₃(10³ + 1) + a₄(10⁴ – 1) + ···.

Since all the numbers 11, 10² – 1, 10³ + 1, · · · are congruent to 0 modulo 11, z – t is also, and therefore z leaves the same remainder on division by 11 as does t. It follows in particular that a number is divisible by 11 (i.e. leaves the remainder 0) if and only if the alternating sum of its digits is divisible by 11. For example, since 3 – 1 + 6 – 2 + 8 – 1 + 9 = 22, the number z = 3162819 is divisible by 11. To find a rule for divisibility by 3 or 9 is even simpler, since 10 ≡ 1 (mod 3 or 9), and therefore 10ⁿ ≡ 1 (mod 3 or 9) for any n. It follows that a number z is divisible by 3 or 9 if and only if the sum of its digits

s = a₀ + a₁ + a₂ + · · · + a_n

is likewise divisible by 3 or 9, respectively.

For congruences modulo 7 we have

10 ≡ 3, 10² ≡ 2, 10³ ≡ –1, 10⁴ ≡ –3, 10⁵ ≡ –2, 10⁶ ≡ 1.

The successive remainders then repeat. Thus z is divisible by 7 if and only if the expression

r = a₀ + 3a₁ + 2a₂ – a₃ – 3a₄ – 2a₅ + a₆ + 3a₇ +...

is divisible by 7.

Exercise: Find a similar rule for divisibility by 13.

In adding or multiplying congruences with respect to a fixed modulus, say d = 5, we may keep the numbers involved from getting too large by always replacing any number a by the number from the set

0, 1, 2, 3, 4

to which it is congruent. Thus, in order to calculate sums and products of integers modulo 5, we need only use the following addition and multiplication tables.

From the second of these tables it appears that a product ab is congruent to 0 (mod 5) only if a or b is ≡ 0 (mod 5). This suggests the general law

7) ab ≡ 0 (mod d) only if either a ≡ 0 or b ≡ 0 (mod d),

which is an extension of the ordinary law for integers which states that ab = 0 only if a = 0 or b = 0. The law 7) holds only when the modulus d is a prime. For the congruence

ab ≡ 0 (mod d)

means that d divides ab, and we have seen that a prime d divides a product ab only if it divides a or b; that is, only if

a ≡ 0 (mod d) or b ≡ 0 (mod d).

If d is not a prime the law need not hold; for we can write d = r.s, where r and s are less than d, so that

r 0 (mod d), s 0 (mod d),

but

rs = d ≡ 0 (mod d).

For example, 2 0 (mod 6) and 3 0 (mod 6), but 2.3 = 6 ≡ 0(mod 6).

Exercise: Show that the following law of cancellation holds for congruences with respect to a prime modulus:

If ab ≡ ac and a 0, then b ≡ c.

Exercises: 1) To what number between 0 and 6 inclusive is the product 11·18·2322·13·19 congruent modulo 7?

2) To what number between 0 and 12 inclusive is 3·7·11·17·19·23·29·113 congruent modulo 13?

3) To what number between 0 and 4 inclusive is the sum 1 + 2 + 2² + · · · +2¹⁰ congruent modulo 5?

2. Fermat’s Theorem

In the seventeenth century, Fermat, the founder of modern number theory, discovered a most important theorem: If p is any prime which does not divide the integer a, then

a^p–1 ≡ 1 (mod p).

This means that the (p — 1)st power of a leaves the remainder 1 upon division by p.

Some of our previous calculations confirm this theorem; for example, we found that 10⁶ ≡ 1 (mod 7), 10² ≡ 1 (mod 3), and 10¹⁰ ≡ 1 (mod 11). Likewise we may show that 2¹² ≡ 1 (mod 13) and 5¹⁰ ≡ 1 (mod 11). To check the latter congruences we need not actually calculate such high powers, since we may take advantage of the multiplicative property of congruences:

To prove Fermat’s theorem, we consider the multiples of a

m₁ = a, m₂ = 2a, m₃ = 3a, · · ·, m_p–1 = (p – 1)a.

No two of these integers can be congruent modulo p, for then p would be a factor of m_r – m_s = (r – s)a for some pair of integers r, s with 1 ≤ r < s ≤ (p – 1). But the law 7) shows that this cannot occur; for since s – r is less than p, p is not a factor of s — r, while by assumption p is not a factor of a. Likewise, none of these numbers can be congruent to 0. Therefore the numbers m₁, m₂, · · ·, m_p–1 must be respectively congruent to the numbers 1, 2, 3, · · ·, p – 1, in some arrangement. It follows that

m₁m₂ · · · m_p–1 = 1·2·3 · · · (p – 1)a^p–1 ≡ 1·2·3 · · · (p – 1) (mod p), or, if for brevity we write K for 1·2·3 · · · (p – 1),

K(a^p–1 – 1) ≡ 0 (mod p).

But K is not divisible by p, since none of its factors is; hence by the law 7), (a^p–1 – 1) must be divisible by p, i.e.

a^p–1 – 1 ≡ 0 (mod p).

This is Fermat’s theorem.

To check the theorem once more, let us take p= 23 and a = 5. We then have, all modulo 23, 5² ≡ 2, 5⁴ ≡ 4, 5⁸ ≡ 16 ≡ –7, 5¹⁶ ≡ 49 ≡ 3, 5²⁰ ≡ 12, 5²² ≡ 24 ≡ 1. With a = 4 instead of 5, we get, again modulo 23, 4² ≡ –7, 4³ ≡ –28 ≡ –5, 4⁴ ≡ –20 ≡ 3, 4⁸ ≡ 9, 4¹¹ ≡ –45 ≡ 1, 4²² ≡ 1.

In the example above with a= 4, p = 23, and in others, we observe that not only the (p – 1)st power of a, but also a smaller power may be congruent to 1. It is always true that the smallest such power, in this case 11, is a divisor of p – 1. (See the following Exercise 3.)

Exercises: 1) Show by similar computation that 2⁸ ≡ 1(mod 17);3⁸ ≡ –1 (mod 17); 3¹⁴ ≡ –1 (mod 29); 2¹⁴ ≡ –1 (mod 29); 4¹⁴ ≡ 1 (mod 29); 5¹⁴≡ 1 (mod 29).

2) Check Fermat’s theorem for p = 5, 7, 11, 17, and 23 with different values of a.

3) Prove the general theorem: The smallest positive integer e for which a^e ≡ 1 (mod p) must be a divisor of p – 1. (Hint: Divide p – 1 by e, obtaining

p – 1 = ke + r,

where 0 ≤ r < e, and use the fact that a^p–1 ≡ a^e ≡ 1 (mod p).)

3. Quadratic Residues

Referring to the examples for Fermat’s theorem, we find that not only is a^p–1 ≡ 1 (mod p) always, but (if p is a prime different from 2, therefore odd and of the form p= 2p’ + 1) that for some values of a, a^p’ = a^(p–1)/2 ≡ 1 (mod p). This fact suggests a chain of interesting investigations. We may write the theorem in the following form:

a^p–1 – 1 = a^2p’ – 1 = (a^p’ – 1)(a^ρ’ + 1) ≡ 0 (mod p).

Since a product is divisible by p only if one of the factors is, it appears immediately that either a^p′ — 1 or a^p′ + 1 must be divisible by p, so that for any prime p > 2 and any number a not divisible by p, either

a^(p–1)/2 ≡ 1 or a^(p–1)/2≡ –1 (mod p).

From the beginning of modern number theory mathematicians have been interested in finding out for what numbers a we have the first case and for what numbers the second. Suppose a is congruent modulo p to the square of some number x,

a ≡ x² (mod p).

Then a^(p–1)/2 ≡ x^p–1, which according to Fermat’s theorem is congruent to 1 modulo p. A number a, not a multiple of p, which is congruent modulo p to the square of some number is called a quadratic residue of p, while a number b, not a multiple of p, which is not congruent to any square is called a quadratic non-residue of p. We have just seen that every quadratic residue a of p satisfies the congruence a^(p–1)/2 ≡ 1 (mod p). Without serious difficulty it can be proved that for every non-residue b we have the congruence b^(p–1)/2 ≡ –1 (mod p). Moreover, we shall presently show that among the numbers 1, 2, 3, · · ·, p– 1 there are exactly (p – 1)/2 quadratic residues and (p – 1)/2 non-residues.

Although much empirical data could be gathered by direct computation, it was not easy at first to discover general laws governing the distribution of quadratic residues and non-residues. The first deeplying property of these residues was observed by Legendre (1752–1833), and later called by Gauss the Law of Quadratic Reciprocity. This law concerns the behavior of two different primes p and q, and states that q is a quadratic residue of p if and only if p is a quadratic residue of q, provided that the product is even. In case product is odd, the situation is reversed, so that p is a residue of q if and only if q is a non-residue of p. One of the achievements of the young Gauss was to give the first rigorous proof of this remarkable theorem, which had long been a challenge to mathematicians. Gauss’s first proof was by no means simple, and the reciprocity law is not too easy to establish even today, although a great many different proofs have been published. Its true significance has come to light only recently in connection with modern developments in algebraic number theory.

As an example illustrating the distribution of quadratic residues, let us choose p = 7. Then, since

0² ≡ 0, 1² ≡ 1, 2² ≡ 4, 3² ≡ 2, 4² ≡ 2, 5² ≡ 4, 6² ≡ 1,

all modulo 7, and since the remaining squares repeat this sequence, the quadratic residues of 7 are the numbers congruent to 1, 2, or 4, while the non-residues are congruent to 3, 5, or 6. In the general case, the quadratic residues of p consist of the numbers congruent to 1², 2², · · ·, (p – 1)². But these are congruent in pairs, for

x² ≡ (p – x)² (mod p) (e.g., 2² ≡ 5² (mod 7)),

since (p – x)² = p² – 2px + x² ≡ x² (mod p). Hence half the numbers 1, 2, · · ·, p – 1 are quadratic residues of p and half are quadratic non-residues.

To illustrate the quadratic reciprocity law, let us choose p = 5, q = 11. Since 11 ≡ 1² (mod 5), 11 is a quadratic residue (mod 5); since the product [(5 – 1)/2][(11 – 1)/2] is even, the reciprocity law tells us that 5 is a quadratic residue (mod 11). In confirmation of this, we observe that 5 ≡ 4²(mod 11). On the other hand, if p = 7, q = 11, the product [(7 – 1)/2][(11 – 1)/2] is odd, and indeed 11 is a residue (mod 7) (since 11 ≡ 2² (mod 7)), while 7 is a non-residue (mod 11).

Exercises: 1. 6² = 36 ≡ 13 (mod 23). Is 23 a quadratic residue (mod 13)?

2. We have seen that x² ≡ (p – x)² (mod p). Show that these are the only congruences among the numbers 1², 2², 3², · · ·, (p – l)².