What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

§7. HAUSDORFF DIMENSION AND FRACTALS

Henri Poincaré’s 1912 definition of dimension (see p. 249) is topological, and—reasonably enough—it always leads to an integer value. A concept of dimension rather different from Poincaré’s has recently come to prominence. It was originally invented by Felix Hausdorff in 1919 and developed by A. S. Besicovitch in the 1930s, but it then became something of a mathematical backwater. It has come back into vogue because of its applications to Benoit Mandelbrot’s theory of fractals—geometric objects with structure on all scales of magnification, such as the famousMandelbrot set (Fig. 288).

This set consists of all complex numbers c (which can be represented as points in the plane) such that the sequence c, c² + c, (c² + c)² + c, … does not tend to infinity. Here each term in the sequence is the square of the previous term, plus c.

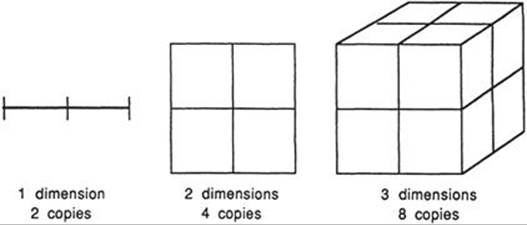
Fig. 289. The number of copies required to double an object’s size depends upon its dimension.

The Hausdorff-Besicovitch dimension of a set, now often called its fractal dimension, has many applications in different branches of science, because it is a precise quantity that can be measured experimentally and compared with theory. Surprisingly, it need not be an integer. This curious feature, the reason why the number is still reasonably considered as a dimension, can be understood by thinking about a simpler version known as scaling dimension, as follows. Some shapes can be assembled to form larger copies of themselves. For example (see Fig. 289), it requires two copies of a line segment (a 1-dimensional object) to make a line segment twice the size. It requires four copies of a (2-dimensional) square to make one twice the size, and it requires eight copies of a (3-dimensional) cube to make one twice the size. In general it requires 2^d copies of a d-dimensional hypercube (see p. 230) to make one twice the size, and it requires c = a^d copies to make one a times the size.

We can solve this equation for c by taking logarithms (see p. 445, equation (6)):

log c = d log a

so that

(6) 

We can now work the other way round and use this equation to define d, given c and a. The result is called the scaling dimension of the set concerned. In examples this leads to intriguing conclusions. For instance, the Cantor set (see p. 248) can be made three times as big (a = 3) by assembling two copies (c = 2) (see Fig. 290).

According to definition (6) the scaling dimension d of the Cantor set is therefore

a real number but not an integer. Similarly the gasket (Fig. 291) can be doubled in size (a = 2) by assembling three copies, so its scaling dimension is

This quantity is called a dimension because it takes the same value as the usual dimension for “nice” sets such as intervals, squares, cubes, and so on. The fractal dimension agrees with the scaling dimension for many sets but is defined for sets that cannot be enlarged by assembling copies of themselves. The fractal dimension of a fractal set is usually not an integer, although sometimes it can be. For example, in 1991 Mitsuhiro Shishikura proved that the fractal dimension of the boundary of the Mandelbrot set is 2. The true significance of the fractal dimension is as a measure of “how well the set fills space” or “how rough the set is.” For example, the Cantor set, with dimension strictly between 0 and 1, fills space better than a point (dimension 0) but less well than a line segment (dimension 1). Thus the fractal dimension resolves the question whether the Cantor set should have dimension 0 or 1 (see p. 249) in a very different manner from Poincaré’s approach.