What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

§11. SOAP FILMS AND MINIMAL SURFACES

Chapter VII, §11 mentions several times the observation that when three soap films meet they appear to form angles of 120°, relating this phenomenon to Steiner’s problem (p. 354). There is a similar phenomenon when four soap film surfaces meet at a common point, as happens in Fig. 240, p. 387: experimentally, the angle formed in the corner of each surface is close to 109°. This is the angle formed by four planes meeting at the centroid of a tetrahedron, as in Fig. 299. Incidentally, this implies that the small central “square” in Fig. 240 is not in fact square, and that in turn explains why the thirteen surfaces in the cubic frame are slightly curved.

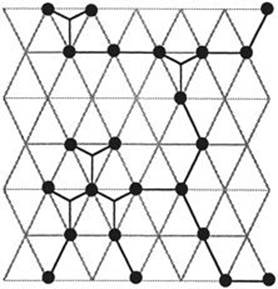
Fig. 298. A Steiner network for towns that lie on a triangular lattice has a much more rigid and regular structure than that for general towns. Du and Hwang reduce the Steiner ratio conjecture to the same problem for lattice networks.

These general rules about angles were first recorded by Plateau, who stated three principles about the form of soap films on frames:

1) They consist of a finite number of flat or smoothly curved surfaces, smoothly joined together.

2) These surfaces meet in only two ways: either exactly three surfaces meet along a smooth curve, or four surfaces meet at a point.

3) When three surfaces meet, the angles between them are 120°, and when four meet, the angles formed in the corners are approximately 109°.

In 1976 Frederick Almgren and Jean Taylor proved that these three properties all follow from a single mathematical principle, the one that forms the basis of Chapter VII, §11: the soap film takes up whatever shape minimizes the total area. Perhaps surprisingly, the difficult step is the first and most qualitative of Plateau’s principles—that the shape consists of a finite number of surfaces. The other two principles follow relatively easily from geometric arguments, just as the 120° angle in Steiner’s problem does. We first indicate this deduction and then discuss the proof of Plateau’s first principle.

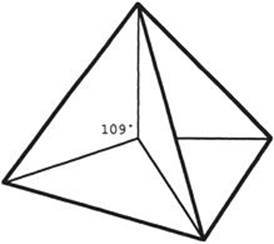
Fig. 299. Minimal surface in a tetrahedral frame: four surfaces meet at the central point, forming angles of 109°.

The first step in the deduction of the second and third principles from the first is to use the smoothness of the surfaces to reduce the problem to one about planes. If a very small region near a line of intersection of three surfaces, or a point of intersection of four, is magnified, then the surfaces appear nearly flat, and the greater the magnification the flatter they seem to be. By thinking about the errors involved in such an approximation, it turns out to be sufficient to prove Plateau’s second and third principle under the simplifying assumption that the surfaces are planar. The second step is to reduce this question to one about lines on a sphere. Consider how the planar regions intersect a sphere centered on the line or point of intersection. The system of planes is then replaced by a system of arcs of great circles (see Fig. 300). The analogue of the requirement of minimum area is that the total length of these arcs should be minimal. By a spherical version of Steiner’s theorem (p. 354), proved in a similar manner, the arcs meet in three at angles of 120°. The third step is to prove that precisely ten different configurations of great circle arcs satisfy these conditions (Fig. 301). The fourth step is to take each such configuration in turn and carry out a search for small deformations of the corresponding configuration of planar surfaces—possibly introducing new pieces—that reduce the total area within the sphere. If any such reduction of area is possible, then the corresponding configuration of arcs can be ruled out: it does not correspond to an arrangement of surfaces of minimal area. (In practice, several of these cases were studied by making corresponding wire frames and observing the shapes formed by soap films in order to deduce the general form of the small deformation involved. Then the possibility of reducing the area was established rigorously by making suitable estimates.) Exactly three configurations survived this process. They comprise a single great circle, three semicircles meeting at 120° angles, and four arcs forming a curvilinear tetrahedron—numbers 1–3 in Fig. 301. The corresponding planar configurations are a single surface not meeting any other, three surfaces meeting at 120° angles, or four surfaces meeting at 109° angles. Plateau’s second and third principles are immediate.

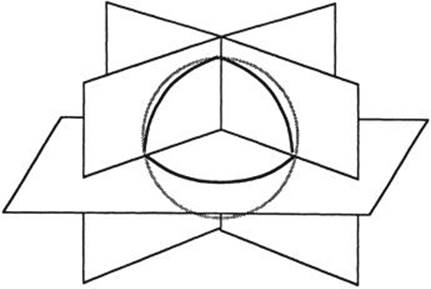
Fig. 300. Reducing the geometry of a system of planes to that of a system of arcs.

Everything thus depends upon proving that the minimal shape consists of finitely many surfaces. In order to achieve this, it is necessary to contemplate the possibility of more complex shapes, and this in turn requires generalizing the concept of area to these more complex shapes. The problem then breaks down into two separate stages. First, prove the existence of some complex shape that minimizes this generalized area. Second, use the minimality property to show that the complex shape is actually fairly simple, composed of finitely many smooth surfaces.

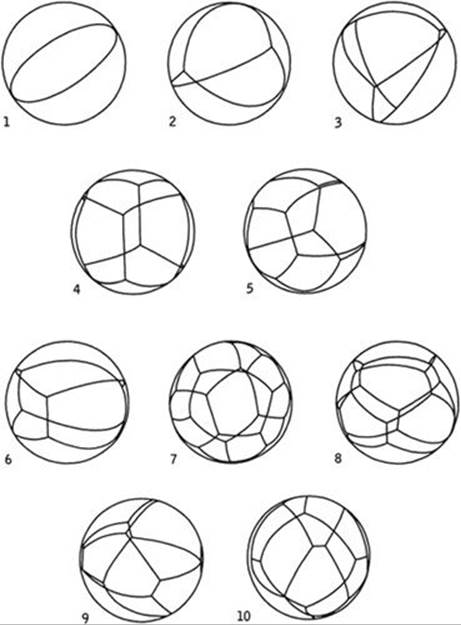
Fig. 301. The ten configurations of arcs that meet at 120° angles. Source: Scientific American 235, no. 1 (July 1976), pp. 90–91.

The techniques for making these two stages work are novel and abstract, belonging to an area known as “geometric measure theory”—the same area that the definition of fractal dimension belongs to. Roughly speaking, any particular surface S is replaced by an associated “measure,” a function that assigns to any region X of space the area of that part of S that lies inside X. More complex shapes are represented by functions with similar properties to these surface-based measures. The advantage of replacing shapes by measures is that measures have much more pleasant properties—for example, they can be added together, or defined as the limit of sequences of other measures, operations that are hard to define directly for geometric shapes.

The existence of a minimizing measure then turns out to be a straightforward argument in geometric measure theory. The more difficult part of the argument is to show that every minimizing measure corresponds to a finite system of smooth surfaces. Ironically, knowledge of how these surfaces would fit together if they really were surfaces—Plateau’s second and third principles—helped Almgren and Taylor to work out how to prove that they actually are surfaces. Knowing in advance what the answer “ought to be” often makes it easier to find a proof.