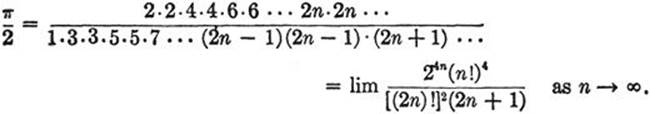What Is Mathematics? An Elementary Approach to Ideas and Methods, 2nd Edition (1996)

Many of the following problems are intended for the somewhat advanced reader. They are designed not so much to develop routine technique as to stimulate inventive ability.

Arithmetic and Algebra

(1) How do we know that 3 does not divide any power of 10, as stated on page 61? (See p. 47.)

(2) Prove that the principle of the smallest integer is a consequence of the theorem of mathematical induction. (See p. 19.)

(3) By the binomial theorem applied to the expansion of (1 + 1)ⁿ, show that .

(*4) Take any integer, z = abe ···, form the sum of its digits, a + b + c + ···, subtract this from z, cross out any one digit from the result, and denote the sum of the remaining digits by w. From a knowledge of w alone, can a rule be found for determining the value of the digit crossed out? (There will be one ambiguous case, when w = 0.) Like many other simple facts about congruences, this can be used as the basis for a parlor trick.

(5) An arithmetical progression of first order is a sequence of numbers, a, a + d, a + 2d, a + 3d, ···, such that the difference between successive members of the sequence is a constant. An arithmetical progression of second order is a sequence of numbers, a₁, a₂, a₃, ··· such that the differences a_i+1 − a_i form an arithmetical progression of first order. Similarly, an arithmetical progression of kth order is a sequence such that the differences form an arithmetical progression of order k − 1. Prove that the squares of the integers form an arithmetical progression of second order, and prove by induction that the kth powers of the integers form an arithmetical progression of order k. Prove that any sequence whose nth term, a_n, is given by the expression c_o + c₁n + c₂n² + ··· + c_kn^k, where the c’s are constants, is an arithmetical progression of order k. *Prove the converse of this statement for k = 2; k = 3; for general k.

(6) Prove that the sum of the first n terms of an arithmetical progression of order k is an arithmetical progression of order k + 1.

(7) How many divisors has 10,296? (See p. 25.)

(8) From the algebraic formula (a² + b²)(c² + d²) = (ac − bd)² + (ad + bc)², prove by induction that any integer r = a¹a² ··· aⁿ, where all the a’s are sums of two squares, is itself a sum of two squares. Check this with 2 = 1² + 1², 5 = 1² + 2², 8 = 2² + 2², etc. for r = 160, r = 1600, r = 1300,r = 625. If possible, give several different representations of these numbers as sums of two squares.

(9) Apply the result of Exercise 8 to construct new Pythagorean number triples from given ones.

(10) Set up rules for divisibility similar to those on page 35 for number systems with the bases 7, 11, 12.

(11) Show that for two positive rational numbers, r = a/b and s = c/d, the inequality r > s is equivalent to ac − bd > 0.

(12) Show that for positive r and s, with r < s, we always have

(13) If z is any complex number, prove by induction that zⁿ + 1/zⁿ can be expressed as a polynomial of degree n in the quantity w = z + 1/z. (See p. 100.)

(*14) Introducing the abbreviation cos φ + i sin φ = E(φ), we have [E(φ)]^m = E(mφ). Use this and the formulas of page 13 on geometrical series, which remain correct for complex quantities, in order to prove that

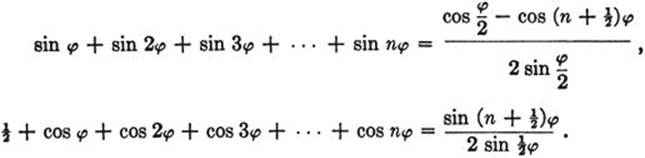
(15) Find what the formula of Exercise 3 on page 18 yields, if we substitute q = E (φ).

Analytic Geometry

A careful study of the following exercises, supplemented by drawings and numerical examples, will help in mastering the elements of analytic geometry. The definitions and simplest facts of trigonometry are presupposed.

It will often be useful to think of a line or a segment as being directed from one of its points toward another. By the directed line PQ (or the directed segment PQ) we shall mean the line (or segment) having the direction from P toward Q. In the absence of explicit specification a directed line l will be supposed to have a fixed but arbitrary direction; except that the directed x-axis will be taken to be directed from 0 toward a point on it with positive x-coördinate, and similarly for the directed y-axis. Directed lines (or directed segments) will then be said to be parallel if and only if they have the same direction. The direction of a directed segment on a directed line can be indicated by attaching a plus or a minus sign to the distance between the endpoints of the segment, according as the segment has the same direction as the line or the opposite direction. It will be desirable to extend the terminology “segment PQ” to the case in which P and Q coincide; to such a “segment” we must clearly assign length zero, but no direction.

(16) Prove: If P₁(x₁, y₁) and P₂(x₂, y₂) are any two points, the coördinates of the midpoint, P₀ (x₀, y₀), of the segment p₁p₂ are x₀ = (x₁ + x₂)/2 y₀ = (y₁ + y₂)/2 More generally, show that, if P₁ and P₂ are distinct, then the point P₀ on the directed line P₁,P₂ for which the ratio P₁P₀: P₁P₂ of the directed lengths has the value k, has the coördinates

x₀ = (1 − k)x₁ + kx₂, y₀ = (1 − k)y₁ + ky₂.

(Hint: Parallel lines cut two transversals in proportional segments.)

Thus the points on the line P¹P² have coördinates of the form x = λ₁x₁ + λ₂x₂, y = λ₁y₂, λ₂y₂ with λ₁ + λ₂ = 1. The values λ₁ = 1 and λ₁ = 0 characterize the points P₁ and P₂ respectively. Negative values of λ₁ characterize points beyond P₂, and negative values of λ₂ characterize points before P₁.

(17) Characterize the position of points on the line in a similar manner by means of the values of k.

It is just as important to use positive and negative numbers to indicate the directions of rotations as of distances. By definition, the direction of rotation that brings the directed x-axis into coincidence with the directed y-axis after a rotation of 90° is taken as positive. In the usual coördinate system, with the positive x-axis directed to the right and the positive y-axis upward, this is the counterclockwise sense of rotation. We now define the angle from a directed line l¹ to a directed line l₂ as the angle through which l₁ must be rotated in order to become parallel to l₂. Of course, this angle is determined only up to integral multiples of a complete revolution of 360°. Thus the angle from the directed x-axis to the directed y-axis is 90° or —270°, etc.

(18) If α is the angle from the directed x-axis to the directed line l, if P₁, P₂ are any two points on l, and if d denotes the directed distance from P₁ to P₂, show that

If the line l is not perpendicular to the x-axis, the slope of l is defined as

The value of m does not depend on the choice of direction on the line, since tan α = tan (α + 180°), or, equivalently, (y₁ − y₂)/(x₁ − x₂) = (y₂ − y₁)/(x₂ − x₁).

(19) Prove: The slope of a line is zero, positive, or negative, according as a parallel to it through the origin lies on the x-axis, in the first and third quadrants, or in the second and fourth quadrants, respectively.

We distinguish a positive and a negative side of a directed line l as follows. Let P be any point not on l, and let Q be the foot of the perpendicular to l through P. Then P is on the positive or negative side of l according as the angle from l to the directed line QP is 90° or −90°.

We shall now determine the equation of a directed line l. We draw through the origin O a line m perpendicular to l, and direct m so that the angle from it to l is 90°. The angle from the directed x-axis to m will be called β. Then α = 90° + β, sin α = cos β, cos α = —sin β. Let R with coördinates x₁, x₂ be the point where m meets l. We shall denote by d the directed distance OR on directed m.

(20) Show that d is positive if and only if 0 lies on the negative side of l.

We have x₁ = d cos β, y₁ = d sin β (compare Ex. 18). Hence, (x − x₁) sin α = (y − y₁) cos α, or (x − d cos β) cos β = − (y − d sin β) sin β, which gives the equation

x cos β + y sin β− d = 0.

This is the normal form of the equation of the line l. Note that this equation does not depend on the direction assigned to l, for a change in direction would change the sign of every term on the left side, and hence would leave the equation unchanged.

By multiplying the normal equation with an arbitrary factor, we obtain the general form of the equation of the line:

ax + by + c = 0.

To retrieve from this general form the geometrically significant normal form we must multiply by a factor which will reduce the first two coefficients to cos β and sin β, whose squares add up to 1. This may be done by the factor which yields the normal form

so that we have

(21) Show: (a) that the only factors that will reduce the general form to the normal form are and ; (b) that the choice of the one or the other of these factors determines which direction is assigned to the line; and (c) that, when one of these factors has been used, the origin is on the positive or negative side of the resulting directed line, or is on the line, according as d is negative, positive, or zero.

(22) Prove directly that the line with slope m through a given point P₀(x₀, y₀) is given by the equation

y − y₀ = m(x − x₀), or y = mx + y₀ − mx₀.

Prove that the line through two given points, P₁(x₁, y₁), P₁(x₂, y₂), has an equation

(y₂ − y₁)(x − x₁) = (x₂ − x₁)(y − y₁).

The x-coördinate of a point in which a line or curve cuts the x-axis is called an x-intercept of the curve; similarly for y-intercept.

(23) By dividing the general equation of Exercise 20 by an appropriate factor, show that the equation of a line may be written in the intercept form,

where a and b are the x- and y-intercepts. What exceptions are there?

(24) By a similar procedure show that the equation of a line not parallel to the y-axis may be written in the slope-intercept form,

y = mx + b.

(If the line is parallel to the y-axis, its equation may be written as x= a.)

(25) Let ax + by + c = 0 and a′x + b′y + c′ = 0 be equations of undirected lines l and l′, with slopes m and m′ respectively. Show that l and l′ are parallel or perpendicular according as: (a) m = m′ or mm′ = −1. (b) ab′ − a′b = 0 or aa′ + bb′= 0. (Note that (b) holds even when a line has no slope, i.e. is parallel to the y-axis.)

(26) Show that the equation of a line through a given point P₀(x₀, y₀) and parallel to a given line l with equation ax + by + c = 0 has the equation ax + by= ax₀ + by₀. Show that a similar formula, bx − ay = bx₀ − ay₀, holds for the equation of the line through P₀ and perpendicular to l. (Note that if the equation of l is in the normal form, so also will the new equation be, in each case.)

(27) Let x cos β+ y sin β− d = 0 and ax + by+ c = 0 be the normal and general forms of the equation of a line l. Show that the directed distance h from l to any point Q(u, v) is given by

h = u cos β + v sin β − d,

or by

and that h is positive or negative according as Q is on the positive or negative side of the directed line l (the direction having been determined by β, or by the choice of the sign before ). (Hint: Write the normal form of the equation of the line m through Q parallel to l, and find the distance from l to m.)

(28) Let l(x, y) = 0 represent the equation ax + by + c = 0 of a line l; similarly for l′(x, y) = 0. Let λ and λ′ be constants, with λ + λ′ = 1. Show that, if l and l′ intersect in P₀(x₀, y₀), then every line through P₀ has an equation

λl(x, y) + λ′l′(x, y) = 0

and conversely; and that every such line is uniquely determined by the choice of a pair of values for λ and λ′. (Hint: P₀ lies on l if and only if l(x₀, y₀) = ax_o + by₀ + c = 0.) What lines are represented if l and l′ are parallel? Note that the condition λ + λ′ = 1 is unnecessary, but serves to determine a unique equation for each line through P₀.

(29) Use the result of the previous exercise to find the equation of a line through the intersection P₀ of l and l′ and through another point, P₁(x₁, y₁), without finding the coördinates of P₀. (Hint: Find λ and λ′ from the conditions λl(x₁, y₁) λ′l′(x₁, y₁) = 0, λ + λ′ = 1) Check by finding the coördinates of P₀ (see pp. 76-77) and showing that P₀ lies on the line whose equation you have found.

(30) Prove that the equations of the bisectors of the angles formed by intersecting lines l and l′ are

(Hint: See Ex. 27.) What do these equations represent if l and l′ are parallel?

(31) Find the equation of the perpendicular bisector of the segment P₁P₂ by each of the following methods: (a) Find the equation of line P₁P₂; find the coördinates of the midpoint P₀ of segment P₁P₂; find the equation of the line through P₀ perpendicular to P₁P₂. (b) Write the equation expressing the fact that the distance (p. 74) between P₁ and any point P(x, y) on the perpendicular bisector is equal to the distance between P₂ and P; square both sides of the equation and simplify.

(32) Find the equation of the circle through three non-collinear points, P₁, P₂, P₃, by each of the following methods: (a) Find the equation of the bisectors of the segments P₁P₂ and P₂P₃; find the coordinates of the center as the point of intersection of these lines; find the radius as the distance between the center and P₁. (b) The equation must be of the form x² + y₂ − 2ax − 2by = k (see p. 74). Since each of the given points lies on the circle we must have

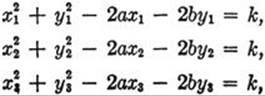
for a point lies on a curve if and only if its coördinates satisfy the equation of the curve. Solve these simultaneous equations for a, b, k.

(33) To find the equation of the ellipse with major axis 2p, minor axis 2q, and foci at F(e, 0) and F(−e, 0), where e² = p² − q², use the distances r and r′ from F and F′ to any point on the curve. By definition of the ellipse, r + r′ = 2p. By using the distance formula on page 74, show that

r′² − r² = (x + e)² − (x − e)² = 4ex.

Since

r′² − r² = (r′ + r)(r′ − r) = 2p(r′ − r),

show that r′ − r= 2ex/p. Solve this relation and r′ + r = 2p to find the important formulas

Since (again by the distance formula) r² = (x − e)² + y², equate this expression for r² to the expression just above,

Expand, collect terms, substitute p² − q² for e², and simplify. Show that the result may be expressed in the form

Carry out the same procedure for the hyperbola, defined as the locus of all points P for which the absolute value of the difference r − r′ is equal to a given quantity 2p. Here e² = p² + q².

(34) The parabola is defined as the locus of a point whose distance from a fixed line (the directrix) is equal to its distance from a fixed point (the focus). If we choose the line x = − a as directrix and the point F(a, 0) as focus, show that the equation of the parabola may be written in the form y² = 4ax.

Geometrical Constructions

(35) Prove the impossibility of constructing with ruler and compass the numbers . Prove that the construction of is only possible if α is the cube of a rational number. (See p. 134, ff.)

(36) Find the sides of the regular 3.2ⁿ-gon and of the 5.2ⁿ-gon and characterize the corresponding sequences of extension fields.

(37) Prove the impossibility of trisecting with ruler and compass an angle of 120 or 30 degrees. (Hint for the case of 30°: The equation to be discussed is . Introduce a new unknown, , and obtain an equation for z from which the non-constructibility of z follows as in the text, p. 139.)

(38) Prove that the regular 9-gon is not constructible.

(39) Prove that the inversion of a point P(x, y) into the point P′(x′, y′) in the circle with the radius r about the origin is given by the equations

Find algebraically the equations giving x, y in terms of x′, y′.

(*40) Prove analytically by using Exercise 39 that by inversion the totality of circles and straight lines is transformed into itself. Check the properties a) - d) on page 142 separately, and likewise the transformations corresponding to Figure 61.

(41) What becomes of the two families of lines, x = const, and y = const., parallel to the coördinate axes, after inversion in the unit circle about the origin? Find the answer without and with analytic geometry. (See p. 160.)

(42) Carry out the Apollonius constructions in simple cases of your own selection. Try the solution analytically according to the method of page 125.

Projective and Non-Euclidean Geometry

(43) Find all the values of the cross ratio λ of four harmonic points, if the points are subjected to permutations. (Answer: λ = −1, 2, ½).

(44) For what configurations of four points do some of the six values of the cross-ratio on page 176 coincide? (Answer: Only for λ = −1 or λ = 1; there is also one imaginary value of λ for which λ = 1/(1 − λ), the “equianharmonic” cross-ratio.)

(45) Show that a cross-ratio (ABCD) = 1 means coincidence of the points C and D.

(46) Prove the statements about the cross-ratio of planes, page 176.

(47) Prove that if P and P′ are inverse with respect to a circle and if the diameter AB is collinear with P, P’, then the points A, B, P, P’ form a harmonic quadruple. (Hint: Use the analytic expression (2) on p. 178, take the circle as the unit circle and AB as the axis.)

(48) Find the coördinates of the fourth harmonic point to three points P₁, P₂, P₃. What happens if P₃ moves to the midpoint of P₁P₂? (See p. 178.)

(*49) Use Dandelin’s spheres to develop the theory of conic sections. In particular prove that they are all (except for the circle) geometrical loci of points whose distances from a fixed point F and a fixed line l have a constant ratio k. For k > 1 we have a hyperbola, for k = 1 a parabola, fork < 1 an ellipse. The line l is obtained by intersecting the plane of the conic with the plane through the circle in which the Dandelin sphere touches the cone. (Since the circle does not come under this characterization except as a limiting case, it is not entirely appropriate to choose this property as a definition of the conics, although this is sometimes done.)

(50) Discuss: “A conic, regarded as both a set of points and a set of lines, is self-dual.” (See p. 209.)

(*51) Try to prove Desargues’s theorem in the plane by carrying out the passage to the limit from the three-dimensional configuration of Figure 73. (See p. 172.)

(*52) How many lines intersecting four given skew lines can be drawn? How can they be characterized? (Hint: Draw a hyperboloid through three of the given lines, see p. 212.)

(*53) If the Poincaré circle is the unit circle of the complex plane, then two points z₁ and z₂ and the z-values w₁, w₂ of the two points of intersection of the “straight line” through these two points with the unit circle define a cross-ratio which, according to Exercise 8 on page 97, is real. Its logarithm is by definition the hyperbolic distance between z₁ and z₂.

(*54) By an inversion transform the Poincaré circle into the upper half plane. Develop the Poincaré model and its properties for this half plane directly and by means of this inversion. (See p. 224.)

Topology

(55) Verify Euler’s formula for the five regular polyhedra and for other polyhedra. Carry out the corresponding network reductions.

(56) In the proof of Euler’s formula (p. 239) we are required to reduce any plane network of triangles, by successive application of two fundamental operations, to a network consisting of a single triangle, for which V − E + F = 3 – 3 + 1 = 1. How can we be sure that the final result will not be a pair of triangles with no vertices in common, so that V – E + F = 6 – 6 + 2 = 2? (Hint: We can assume that the original network is connected, i.e. that one can pass from any vertex to any other along edges of the network. Show that this property cannot be destroyed by the two fundamental operations.)

(57) We have admitted only two fundamental operations in the reduction of the network. Might it not happen at some stage that a triangle appears having only one vertex in common with the other triangles of the network? (Construct an example.) This would require a third operation: Removal of two vertices, three edges, and a face. Would this affect the proof?

(58) Can a wide rubber band be wrapped three times around a broomstick so as to lie flat (i.e. untwisted) on the broomstick? (Of course, the rubber band must cross itself somewhere.)

(59) Show that a circular disk from which the point at the center has been removed admits a continuous, fixed-point-free transformation into itself.

(*60) The transformation which shifts each point of a disk one unit in a fixed direction obviously has no fixed points. Of course, this is not a transformation of the disk into itself, since some points will be taken into points outside the disk. Why does not the argument of page 255, based on the transformation P → P*, hold in this case?

(61) Suppose we have a rubber inner tube, the inside of which is painted white and the outside black. Is it possible, by cutting a small hole, deforming the tube, and then sealing up the hole, to turn the tube inside out, so that the inside will be black and the outside white?

(*62) Show that there is no “four color problem” in three dimensions by proving that for any desired number n, n bodies can be placed in space so that each touches all the others.

(*63) Using either an actual torus surface (inner tube, anchor ring) or a plane region with boundary identification (Fig. 143), construct a map consisting of seven regions, each of which touches all the others. (See p. 248.)

(64) The 4-dimensional tetrahedron of Figure 118 consists of five points, a, b, c, d, e, each of which is joined to the other four. Even if the connecting lines are allowed to be curved, the figure cannot be drawn in the plane in such a way that no two of the connections cross. Another configuration, containing ten connections, that cannot be drawn in the plane without crossings consists of six points, a, b, c, a′, b′, c′, such that each of the points a, b, c, is connected to each of the points a′, b′, c′. Verify these facts by experiment, * and try to devise a proof, using the Jordan curve theorem as a basis. (It has been proved that any configuration of points and lines that cannot be represented in the plane without crossings must contain one of these two configurations as a part.)

(65) A configuration is formed by taking the six sides of a 3-dimensional tetrahedron and adding one line joining the midpoints of two opposite sides. (Two sides of a tetrahedron are opposite if they have no common endpoint.) Show that this configuration is equivalent to one described in the preceding exercise.

(*66) Let p, q, r be the three tips of the symbol E. The symbol is shifted some distance away, giving another E, with tips p′, q′, r′. Can one join p to p′, q to q′, and r to r′ by three curves which do not cross each other or the E’s?

If we go around a square, we change our direction four times, each time by an amount 90°, giving a total change of Δ = 360°. If we go around a triangle, it is known from elementary geometry that Δ = 360°.

(67) Prove that if C is any simple closed polygon, then Δ = 360°. (Hint: Cut the interior of C into triangles, then remove boundary segments, as on p. 239. Let the successive boundaries be B₁, B₂, B₃,..., B_n. Then B₁ = C, and B_n is a triangle. Show that, if Δ_i corresponds to B_i, then Δ_i, = Δ_i–1.)

(*68) Let C be any simple closed curve with a continuously turning tangent vector. If Δ denotes the total change in the angle of the tangent as we traverse the curve once, show that here also Δ = 360°. (Hint: Let p₀, p₁, p₂,..., p_n, p₀ be points cutting C into small, nearly straight segments. Let C_i be the curve with the segments p₀p₁, p₁p₂,..., p_i–1p_i, and the original arcs p_ip_i+1,..., p_np₀. Then C₀ = C, and C_n is composed of line segments. Show that Δ_i = Δ_i+1, and use the result of the preceding exercise). Does this apply to the hypocycloid of Figure 55?

(68) Show that if in the diagram of the Klein bottle on page 263 all four arrows are drawn clockwise, a surface is formed that is equivalent to a sphere with one disk replaced by a cross-cap. (This surface is topologically equivalent to the extended plane of projective geometry.)

(70) The Klein bottle of Figure 142 may be cut into two symmetrical halves by a plane. Show that the result consists of two Moebius strips.

(*71) In the Moebius strip of Figure 139 the two endpoints of each transversal segment are identified. Show that the result is topologically equivalent to a Klein bottle.

All possible ordered pairs of points on a line segment (the two points coinciding or not) form a square, in the following sense. If the points of the segment are designated by their distances x, y from one end A, the ordered pairs of numbers (x, y) may be regarded as the Cartesian coördinates of a point of the square.

All possible pairs of points without regard to order (i.e. with (x, y) regarded as the same as (y, x)) form a surface S which is topologically equivalent to a square. To see this choose that representation which has the first point nearest the end A of the segment, if x ≠ y. Thus S is the set of all pairs (x, y) where either x is less than y or x = y. Using Cartesian coördinates, this gives the triangle in the plane with vertices (0, 0), (0, 1), (1, 1).

(*72) What surface is formed by the set of all ordered pairs of points of which the first belongs to a line and the second to the circumference of a circle? (Answer: A cylinder.)

(73) What surface is formed by the set of all ordered pairs of points on a circle? (Answer: A torus.)

(*74) What surface is formed by the set of all unordered pairs of points on a circle? (Answer: A Moebius strip.)

(75) Here are the rules of a game, played with pennies on a large circular table: A and B in turn place pennies on the table. The pennies need not touch each other, and a penny may be placed anywhere on the table, so long as it does not extend over the edge or overlap a penny already on the table. Once placed, a penny may not be moved. In time, the table will be covered with pennies in such a way that no space large enough for another penny remains. The player who is able to place the last penny on the table wins. If A plays first, prove that no matter how B plays, A can be sure of winning, provided that he plays correctly.

(76) If, in the game of Exercise 75 the table has the form of Figure 125, b, prove that B can always win.

Functions, Limits and Continuity

(77) Find the continued fraction expansion for the ratio OB:AB of page 123.

(78) Show that the sequence is monotone increasing, bounded by B = 2, and hence has a limit. Show that this limit must be the number 2. (See pp. 125 and 326.)

(*79) Try to prove, by methods similar to those used on pages 318 and following, that given any smooth closed curve, a square may always be drawn whose sides are tangent to the curve.

The function u = f(x) is called convex if the midpoint of the segment joining any two points of the graph of the function lies above the graph. For example, u = e^x (Fig. 278) is convex, while u = log x (Fig. 277) is not.

(80) Prove that the function u = f(x) is convex if, and only if,

with equality only for x₁ = x₂.

(*81) Prove that for convex functions the more general inequality

λ₁f(x₁) + λ₂f(x₂) ≥ f(λ₁x₁ + λ₂x₂)

holds, where λ₁, λ₂ are any two constants such that λ₁ + λ₂ = 1 and λ₁ ≥ 0, λ₂ ≥ 0. This is equivalent to the statement that no point of the segment joining two points of the graph lies below the graph.

(82) Using the condition of Exercise 80 prove that the functions and u = 1/x (for x > 0) are convex, i.e. that

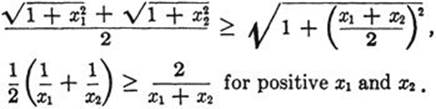
(83) The same for u = x², u = xⁿ for x > 0, u = sin x for π ≤ x ≤ 2π, u = tan x for 0 ≤ x ≤ π/2, for | x | ≤ 1.

Maxima and Minima

(84) Find the path of shortest length between P and Q as in Figure 178, if the path is supposed to meet the two given lines alternately n times. (See p. 333.)

(85) Find the shortest connection between two points P and Q within a triangle with acute angles if the path is required to meet the sides of the triangle in a given order. (See p. 334.)

(86) Draw the level lines and check the existence of at least two saddle points in a surface over a triply connected domain whose boundary is on the same level. (See p. 345.) Again we must exclude the case where the tangent plane to the surface is horizontal along a whole closed curve.

(87) Starting with two arbitrary positive rational numbers, a and b, form, step by step, the pairs. . Prove that they define a sequence of nested intervals. (The limit point as n→ ∞, the so-called arithmetical-geometrical mean of a_o and b_o, played a great rôle in the early researches of Gauss).

(88) Find the length of the whole graph in Figure 219, and compare this with the total length of the two diagonals.

(*89) Investigate conditions on four points, A₁, A₂, A₃, A₄, that show whether they lead to the case of Figure 216 or 218.

(*90) Find systems of five points for which different street nets satisfying the angular conditions exist. Only some of them will yield relative minima. (See p. 361.)

(91) Prove Schwarz’s inequality,

valid for any set of pairs of numbers a_i, b_i,; prove that the inequality sign holds only if the a_i are proportional to the b_i. (Hint: Generalize the algebraic formula of Ex. 8.)

(*92) With n positive numbers x_i,..., x_n we form the expressions S_k defined by

where the symbol “+...” means that all the Cⁿ_k products of combinations of k of these quantities are to be added. Then prove that

where the equality sign holds only if all the quantities x_i are equal.

(93) For n = 3 these inequalities state that for three positive numbers a, b, c

What extremal properties of the cube are implied by these inequalities?

(*94) Find an arc of a curve of shortest length joining two points A, B and including with the segment AB a prescribed area. (Answer: The arc must be circular.)

(*95) Given two segments AB and A’B’, find an arc joining A to B and one joining A’ to B’ such that the two arcs include with the two segments a prescribed area and have a minimum total length. (Answer: The arcs are circular with the same radius.)

(*96) The same for any number of segments, AB, A’B’, etc.

(*97) On two lines intersecting at O find two points A and B, respectively, and join A with B by an arc of minimal length such that the area included by it and the lines is prescribed. (Answer: The arc is circular and perpendicular to the lines.)

(*98) The same problem, but now the total perimeter of the domain included, i.e. the arc plus OA plus OB is to be a minimum. (Answer: The solution is given by an arc of a circle which bulges outward and touches the two lines.)

(*99) The same problem for several angular sectors.

(*100) Prove that the nearly plane surfaces in Figure 240 are not plane except for the stabilizing surface in the center. Remark: To find or characterize these curved surfaces analytically is a challenging unsolved problem. The same is true for the surfaces in Figure 251. In Figure 258 we actually have twelve symmetric planes meeting at 120° in the diagonals.

Advice for some additional soap film experiments. Carry out experiments indicated by Figures 256 and 257 for more than three connecting rods. Study the limiting cases for volume of air tending to zero. Experiment with non-parallel planes or other surfaces. Blow up the cubic bubble ofFigure 258 until it fills the whole cube and bulges over the edges. Then suck the air out again, reversing the process.

(*101) Find two equilateral triangles with given total perimeter and minimum area. (Answer: The triangles must be congruent (use calculus).)

*(102) Find two triangles with given total perimeter and maximum area. (Answer: One triangle degenerates into a point; the other one must be equilateral.)

*(103) Find two triangles with given total area and minimum perimeter.

(*104) Find two equilateral triangles with given total area and maximum perimeter.

The Calculus

(105) Differentiate the functions by applying directly the definition of derivative, forming and transforming the difference quotient until the limit can be obtained easily by substituting x₁ = x. (Sec p. 421.)

(106) Prove that the function with y = 0 for x = 0, has all its derivatives zero at x= 0.

(107) Show that the function of Exercise 106 cannot be expanded in a Taylor series. (See p. 477.)

(108) Find the points of inflection (f″(x) = 0) of the curves y = e^–x2 and y = xe^–x2

(109) Prove that for a polynomial f(x) with all n roots x₁,...,x_n distinct we have

*(110) Using the direct definition of the integral as limit of a sum, prove that for n → ∞ we have

(*111) Prove in a similar way that

(112) By drawing Figure 276 in large scale on coördinate paper and counting the small squares in the shaded area, find an approximate value for π.

(113) Use formula (7), page 441 for the numerical calculation of π with a guaranteed accuracy of at least 1/100.

(114) Prove: e^{π i} = –1. (See p. 478.)

(115) A curve of given shape is expanded in the ratio 1:x. L(x) and A(x) denote the length and area of the expanded curve. Show that L(x)/A(x)→ 0 as x→ ∞ and, more generally, L(x)/A(x)^k → 0 as x→ ∞, if . Check for circle, square and, * ellipse. (Area is of a higher order of magnitude than circumference. See p. 472.)

(116) Often the exponential function occurs in combinations given and denoted as follows:

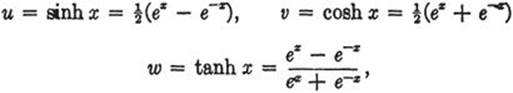
called hyperbolic sine, hyperbolic cosine, and hyperbolic tangent respectively. These functions have many properties analogous to those of the trigonometric functions; they are linked to the hyperbola u² − v² = 1 much as the functions u = cos x and v = sin x are linked to the circle u² + v² = 1. The following facts should be proved by the reader and compared with the corresponding facts concerning trigonometric functions:

D cosh x = sinh x, D sinh x = cosh x, D tanh x = l/cosh²x,

 sinh (x + x′)= sinh x · cosh x′ + cosh x sinh x′,

 cosh (x + x′) = cosh x·cosh x′ + sinh x· sinh x′.

The inverse functions are called x = arc sinh ; .

Their derivatives are given by

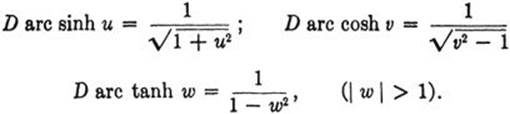
(117) On the basis of Euler’s formula check the analogy between hyperbolic and trigonometric functions.

(*118) Find simple summation formulas for

sinh x + sinh 2x +... + sinh nx

and

½ + cosh x + cosh 2x +... + cosh nx

analogous to those in Exercise 14 for trigonometric functions.

Technique of Integration

The theorem of p. 439 reduces the problem of integrating a function f(x) between the limits a and b to that of finding a primitive function G(x) for f(x), i.e. one for which G’(x) = f(x). The integral is then simply the difference G(b) − G(a). For these primitive functions, which are determined by f(x) (except for an arbitrary additive constant), the name “indefinite integral” and the suggestive notation

without limits of integration, is customary. (This notation may be misleading for the beginner; see the remark on p. 438.)

Every formula of differentiation contains the solution of a problem of indefinite integration simply by interpreting it inversely as a formula of integration. We can extend this somewhat empirical procedure by two important rules, which are nothing but the equivalent of the rules of differentiation of a compound function and of a product of functions. In their integral form these are called the rules of integration by substitution and integration by parts.

A) The first rule results from the formula for the differentiation of a compound function,

H(u) = G(x),

where

x = ψ(u) and u = φ(x)

are supposed to be functions of each other, uniquely determined in the interval under consideration. Then we have

H′(u) = G′(x)ψ′(u).

If

G′(x) = f(x),

we can write

and also

G′(x)ψ′(u) = f(x)ψ′(u),

which, in consequence of the formula above for H′(u), is equivalent to

Hence, since H(u) = G(x),

(I) 

Written in Leibniz’ notation (see p. 434) this rule takes the very suggestive form

which means that the symbol dx may be replaced by the symbol , just as if dx and du were numbers and a fraction.

The usefulness of formula (I) will be illustrated by a few examples.

a) . Here we start with the right hand side of (I), substituting x = log u = ψ(u). We then have ; hence

or

We can verify this result by differentiating both sides. We find, , which is easily shown to be correct.

b)

hence,

or

This result can again be verified by differentiation.

c) In general, if we have an integral of the form

we set x= ψ(u), f(x) = x and find

d)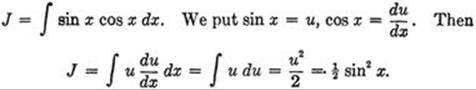

e)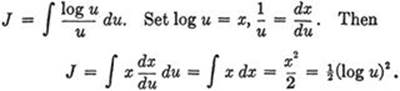

In the examples below (I) is used, starting from the left side.

f)

fore

g) By the substitution x = au, where a is a constant, we find

h)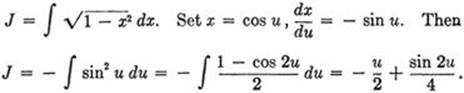

Using , we have

Evaluate the following indefinite integrals and verify the results by differentiation:

119)

120)

121)

122)

123)

124)

125)

126)

127)

128)

129)

(Compare examples g, h.)

B) The rule (p. 428) for the differentiation of a product,

(p(x)·q(x))′ = p(x)·q′(x) + p′(x)·q(x),

can be written as an integral formula:

or

(II) 

In this form it is called the rule of integration by parts. This rule is useful when the function to be integrated can be written as a product of the form p(x)q′(x), where the primitive function q(x) of q′(x) is known. In that case formula (II) reduces the problem of finding the indefinite integral ofp(x)q′(x) to that of the integration of the function p′(x)q(x), which is often much simpler to solve.

Examples:

a)

Then (II) leads to

b)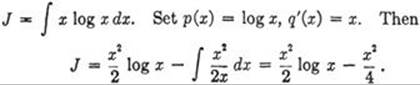

c)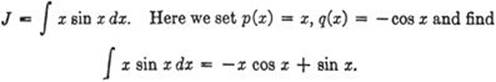

Evaluate the following integrals using integration by parts.

130)

131)

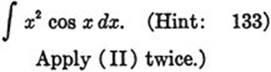
132)

133)

Integration by parts of the integral leads to a remarkable expression for the number π as an infinite product. To derive it we write the function sin^m x in the form sin^m−1·sin x and integrate by parts between the limits 0 and π/2. This leads to the formula

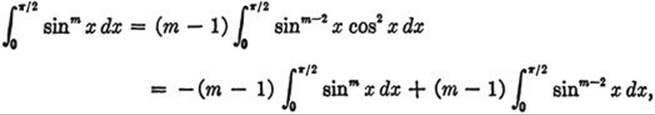
or

because the first term on the right side of (II), pq, is equal to zero for the values 0 and π/2. By repeated application of the last formula we find the following value for (the formulas differ according as m is even or odd):

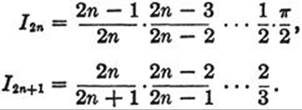
Since 0 < sin x < 1 for 0 < x < π/2, we have sin^2n–1 x > sin²ⁿ x > sin²ⁿ⁺¹ x, so that

I_2n–1 > I_2n > I_2n+1 (see p. 414)

or

Substituting the values calculated above for l_2n-1, etc. in the last inequalities, we find

If we now pass to the limit as n→ ∞ we see that the middle term tends to 1, hence we obtain Wallis’ product representation for π/2: