Stability of Linear Systems - Basic Difference Calculus

Discrete Fractional Calculus (2015)

1. Basic Difference Calculus

1.10. Stability of Linear Systems

At the outset of this section we will be concerned with the stability of the trivial solution of the vector difference equation

$\displaystyle{ y(t + 1) = Ay(t),\quad t \in \mathbb{N}_{a}, }$

(1.48)

where A is an n × n constant matrix. By the trivial solution of (1.48) we mean the solution y(t) ≡ 0, $t \in \mathbb{N}_{a}$ (here by context we know 0 denotes the zero vector). First we define what we mean by the stability of the trivial solution on $\mathbb{N}_{a}.$ We will adopt the notation that y(t, z) denotes the unique solution of the IVP

$\displaystyle{y(t + 1) = Ay(t),\quad y(a) = z,\quad z \in \mathbb{R}^{n}.}$

Definition 1.94.

Let $\|\cdot \|$ be a norm on $\mathbb{R}^{n}$ . We say the trivial solution of (1.48) is stable on $\mathbb{N}_{a}$ provided given any ε > 0, there is a δ > 0 such that $\|y(t,z)\| <\epsilon$ on $\mathbb{N}_{a}$ if $\|z\| <\delta.$ If this is not the case we say the trivial solution of (1.48) is unstableon $\mathbb{N}_{a}$ . If the trivial solution is stable on $\mathbb{N}_{a}$ and $\lim _{t\rightarrow \infty }y(t) = 0$ for every solution y of (1.48), then we say the trivial solution of (1.48) is globally asymptotically stable on $\mathbb{N}_{a}$ .

We will use the following remark in the proof of the next theorem.

Remark 1.95.

An important result [137, Theorem 2.54] in analysis gives that for any n × n constant matrix M, there is a constant D > 0, depending on M and the norm $\|\cdot \|$ on $\mathbb{R}^{n}$ , so that

$\displaystyle{\|Mz\| \leq D\|z\|}$

for all $z \in \mathbb{R}^{n}$ .

Theorem 1.96.

If the eigenvalues of A satisfy $\vert \lambda _{k}\vert < 1$ , 1 ≤ k ≤ n, then the trivial solution of (1.48) is globally asymptotically stable on $\mathbb{N}_{a}$ .

Proof.

We will just prove this theorem for the case a = 0. Let $r:=\max \{ \vert \lambda _{k}\vert: 1 \leq k \leq n\}$ and fix δ so that 0 ≤ r < δ < 1. From the Putzer algorithm (Theorem 1.88), the solution y(t, z) of (1.48) satisfying y(0, z) = z is given by

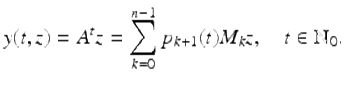
$\displaystyle{ y(t,z) = A^{t}z =\sum _{ k=0}^{n-1}p_{ k+1}(t)M_{k}z,\quad t \in \mathbb{N}_{0}. }$

(1.49)

We now show that for each 1 ≤ k ≤ n there is a constant B _k > 0 such that

$\displaystyle{ \vert p_{k}(t)\vert \leq B_{k}\delta ^{t},\quad t \in \mathbb{N}_{ 0}. }$

(1.50)

By (1.44),

$\displaystyle{\vert p_{1}(t + 1)\vert \leq r\vert p_{1}(t)\vert,\quad t \in \mathbb{N}_{0}.}$

Iterating this inequality and using p ₁(0) = 1, we have

$\displaystyle{\vert p_{1}(t)\vert \leq r^{t},\quad t \in \mathbb{N}_{ 0}.}$

Hence if we let B ₁ = 1 and use the fact that r < δ we have that

$\displaystyle{\vert p_{1}(t)\vert \leq B_{1}\delta ^{t},\quad t \in \mathbb{N}_{ 0}.}$

Hence (1.50) holds for k = 1. We next show that there is a constant B ₂ > 0 such that

$\displaystyle{\vert p_{2}(t)\vert \leq B_{2}\delta ^{t},\quad t \in \mathbb{N}_{ 0}.}$

From (1.44) we get

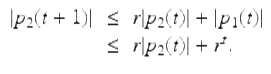
$\displaystyle\begin{array}{rcl} \vert p_{2}(t + 1)\vert & \leq & r\vert p_{2}(t)\vert + \vert p_{1}(t)\vert {}\\ &\leq & r\vert p_{2}(t)\vert + r^{t}. {}\\ \end{array}$

It follows from iteration and p ₂(0) = 0 that

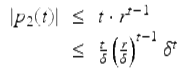
$\displaystyle\begin{array}{rcl} \vert p_{2}(t)\vert & \leq & t \cdot r^{t-1} {}\\ & \leq & \frac{t} {\delta } \left (\frac{r} {\delta } \right )^{t-1}\delta ^{t} {}\\ \end{array}$

for $t \in \mathbb{N}_{0}$ . L’Hôpital’s rule implies that

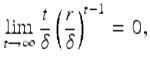
$\displaystyle{\lim _{t\rightarrow \infty }\frac{t} {\delta } \left (\frac{r} {\delta } \right )^{t-1} = 0,}$

so there is a constant B ₂ > 0 so that

$\displaystyle{\vert p_{2}(t)\vert \ \leq \ B_{2}\delta ^{t},\quad t \in \mathbb{N}_{ 0}.}$

Hence (1.50) holds for k = 2. Similarly, we can show that for $t \in \mathbb{N}_{0}$

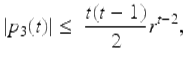
$\displaystyle{\vert p_{3}(t)\vert \leq \ \frac{t(t - 1)} {2} r^{t-2},}$

from which it follows that there is a B ₃ so that

$\displaystyle{\vert p_{3}(t)\vert \leq \ B_{3}\delta ^{t},\quad t \in \mathbb{N}_{ 0}.}$

Continuing in this manner, we obtain constants B _k > 0, 1 ≤ k ≤ n so that

$\displaystyle{\vert p_{k}(t)\vert \leq B_{k}\delta ^{t},\quad t \in N_{ 0},}$

for k = 1, 2, ⋯ , n. Using Remark 1.95 we have there are constants D _ksuch that

$\displaystyle{\|M_{k}z\| \leq D_{k}\|z\|,\quad 1 \leq k \leq n}$

for all $z \in \mathbb{R}^{n}.$ Using this and (1.49) we have that for $t \in \mathbb{N}_{0}$ ,

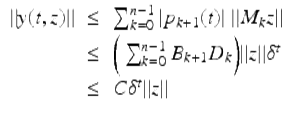
$\displaystyle\begin{array}{rcl} \|y(t,z)\|& \leq & \sum _{k=0}^{n-1}\vert p_{ k+1}(t)\vert \;\|M_{k}z\| \\ & \leq & \bigg(\sum _{k=0}^{n-1}B_{ k+1}D_{k}\bigg)\|z\|\delta ^{t} \\ & \leq & C\delta ^{t}\|z\| {}\end{array}$

(1.51)

where $C:=\sum _{ k=0}^{n-1}B_{k+1}D_{k}$ . It follows from (1.51) that the trivial solution is stable on $\mathbb{N}_{0}$ . Since 0 < δ < 1, it also follows from (1.51) that $\lim _{t\rightarrow \infty }y(t,z) = 0$ . Hence the trivial solution of (1.48) is globally asymptotically stable on $\mathbb{N}_{0}$ . □

Example 1.97.

Consider the vector difference equation

$\displaystyle{ u(t+1) = \left [\begin{array}{ll} \;\;1 & - 5\\.25 & - 1 \end{array} \right ]u(t). }$

(1.52)

The characteristic equation for $A = \left [\begin{array}{ll} \;\;1 & - 5\\.25 & - 1 \end{array} \right ]$ is $\lambda ^{2} + \frac{1} {4} = 0$ and hence the eigenvalues of A are $\lambda _{1} = \frac{i} {2}$ and $\lambda _{2} = -\frac{i} {2}$ . Since

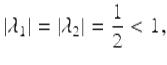
$\displaystyle{\vert \lambda _{1}\vert = \vert \lambda _{2}\vert = \frac{1} {2} < 1,}$

we have by Theorem 1.96 the trivial solution of (1.52) is globally asymptotically stable on $\mathbb{N}_{0}$ .

In the next theorem we give conditions under which the trivial solution of (1.48) is unstable on $\mathbb{N}_{a}$ .

Theorem 1.98.

If there is an eigenvalue, $\lambda _{0}$ , of A satisfying $\vert \lambda _{0}\vert > 1$ , then the trivial solution of (1.48) is unstable on $\mathbb{N}_{a}$ .

Proof.

Assume $\lambda _{0}$ is an eigenvalue of A so that $\vert \lambda _{0}\vert > 1$ . Let v ₀ be a corresponding eigenvector. Then $y_{0}(t) =\lambda _{ 0}^{t-a}v_{0}$ is a solution of equation (1.48) on $\mathbb{N}_{a}$ , and

$\displaystyle{\lim _{t\rightarrow \infty }\|y_{0}(t)\| =\lim _{t\rightarrow \infty }\vert \lambda \vert ^{t-a}\|v_{ 0}\| = \infty.}$

This implies that the trivial solution of (1.48) is unstable on $\mathbb{N}_{a}$ . □

Example 1.99.

Consider the vector difference equation

$\displaystyle{ y(t+1) = \left [\begin{array}{ll} -.5&\;\;\;3\\ \;\;\;.5 & - 1 \end{array} \right ]y(t). }$

(1.53)

The characteristic equation for $A = \left [\begin{array}{ll} -.5&\;\;\;3\\ \;\;\;.5 & - 1 \end{array} \right ]$ is $\lambda ^{2} + \frac{3} {2}\lambda - 1 = 0$ and so the eigenvalues are $\lambda _{1} =.5,$ $\lambda _{2} = -2,$ Since $\vert \lambda _{2}\vert = 2 > 1$ we have by Theorem 1.98 that the trivial solution of (1.53) is unstable on $\mathbb{N}_{0}.$

In the next theorem we give conditions on the matrix A which implies the trivial solution is stable on $\mathbb{N}_{0}$ .

Theorem 1.100.

Let $\lambda _{1},\lambda _{2},\ldots,\lambda _{n}$ be the eigenvalues of A. Assume $\vert \lambda _{k}\vert \leq 1$ and whenever $\vert \lambda _{k}\vert = 1$ , then $\lambda _{k}$ is a simple eigenvalue of A. Then the trivial solution of (1.48) is stable on $\mathbb{N}_{a}$ .

Proof.

We prove this theorem for the case a = 0. If all the eigenvalues of A satisfy $\vert \lambda _{i}\vert < 1$ , then by Theorem 1.96 we have that the trivial solution of (1.48) is stable on $\mathbb{N}_{0}$ . Now assume there is at least one eigenvalue of A with modulus one. Without loss of generality we can order the eigenvalues of A so that $\vert \lambda _{i}\vert = 1$ for $i = 1,\ldots,k - 1$ , where 2 ≤ k ≤ n and $\vert \lambda _{i}\vert < 1$ for $i = k,\ldots,n$ . From equations (1.44) and (1.45),

$\displaystyle{p_{1}(t) =\lambda _{ 1}^{t}.}$

Next, p ₂ satisfies

$\displaystyle{p_{2}(t + 1) =\lambda _{2}p_{2}(t) +\lambda _{ 1}^{t},}$

so (as in the annihilator method)

$\displaystyle{(E -\lambda _{1}I)(E -\lambda _{2}I)p_{2}(t) = 0.}$

Since $\lambda _{1}\neq \lambda _{2}$ ,

$\displaystyle{p_{2}(t) = B_{12}\lambda _{1}^{t} + B_{ 22}\lambda _{2}^{t},}$

for some constants B ₁₂, B ₂₂. Continuing in this way, we have

$\displaystyle{p_{i}(t) = B_{1i}\lambda _{1}^{t} +\ldots +B_{ ii}\lambda _{i}^{t}}$

for $i = 1,\ldots,k - 1$ . Consequently, there is a constant D > 0 so that

$\displaystyle{\vert p_{i}(t)\vert \leq D}$

for $i = 1,\ldots,k - 1$ and $t \in \mathbb{N}_{0}$ .

From (1.44), $p_{k}(t + 1) =\lambda _{k}p_{k}(t) + p_{k-1}(t)$ and hence

$\displaystyle{\vert p_{k}(t + 1)\vert \leq \vert \lambda _{k}\vert \vert p_{k}(t)\vert + D,\quad t \in \mathbb{N}_{0}.}$

Choose $\delta =\max \{ \vert \lambda _{k}\vert,\vert \lambda _{k+1}\vert,\ldots,\vert \lambda _{n}\vert \} < 1$ . Then

$\displaystyle{\vert p_{k}(t + 1)\vert \leq \delta \vert p_{k}(t)\vert + D.}$

By iteration and the initial condition p _k(0) = 0,

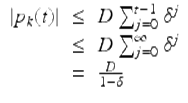
$\displaystyle\begin{array}{rcl} \vert p_{k}(t)\vert & \leq & D\sum _{j=0}^{t-1}\delta ^{j} {}\\ & \leq & D\sum _{j=0}^{\infty }\delta ^{j} {}\\ & =& \frac{D} {1-\delta } {}\\ \end{array}$

for $t \in \mathbb{N}_{0}$ . In a similar manner, we find that there is a constant D ^∗ so that

$\displaystyle{\vert p_{i}(t)\vert \leq D^{{\ast}}}$

for $i = 1,2,\ldots,n$ and $t \in \mathbb{N}_{0}$ .

From Theorem 1.88, the solution of equation (1.48) satisfying u(0) = u ₀, is given by

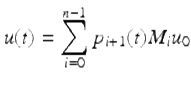
$\displaystyle{u(t) =\sum _{ i=0}^{n-1}p_{ i+1}(t)M_{i}u_{0}}$

and it follows that

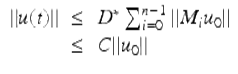
$\displaystyle\begin{array}{rcl} \|u(t)\|& \leq & D^{{\ast}}\sum _{ i=0}^{n-1}\|M_{ i}u_{0}\| \\ & \leq & C\|u_{0}\| \\ \end{array}$

for $t \in \mathbb{N}_{0}$ and some C > 0. □

Example 1.101.

Consider the system

$\displaystyle{ u(t+1) = \left [\begin{array}{ll} \;\;\;\cos \theta &\sin \theta \\ -\sin \theta &\cos \theta \end{array} \right ]u(t),\quad t \in \mathbb{N}_{ a}, }$

(1.54)

where $\theta$ is a real number. For each $\theta$ the eigenvalues of the coefficient matrix in (1.54) are $\lambda _{1,2} = e^{\pm i\theta }.$ Since $\vert \lambda _{1}\vert = \vert \lambda _{2}\vert = 1$ and both eigenvalues are simple, we have by Theorem 1.100 that the trivial solution of (1.54) is stable on $\mathbb{N}_{a}$ . From linear algebra the coefficient matrix in (1.54) is called a rotation matrix. When a vector u is multiplied by this coefficient matrix, the resulting vector has the same length as u, but its direction is $\theta$ radians clockwise from u. Consequently, every solution u of the system has all of its values on a circle centered at the origin of radius | u(a) | . This also tells us that the trivial solution of (1.54) is stable on $\mathbb{N}_{a},$ but not globally asymptotically stable on $\mathbb{N}_{a}.$