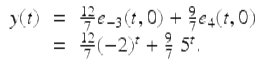The Convolution Product - Discrete Delta Fractional Calculus and Laplace Transforms - Discrete Fractional Calculus

Discrete Fractional Calculus (2015)

2. Discrete Delta Fractional Calculus and Laplace Transforms

2.6. The Convolution Product

The following definition of the convolution product agrees with the convolution product defined for general time scales in [62], but it differs from the convolution product defined by Atici and Eloe in [32] (in the upper limit). We demonstrate several advantages of using Definition 2.59 in the following results.

Definition 2.59.

Let $$f,g: \mathbb{N}_{a} \rightarrow \mathbb{R}$$ be given. Define the convolution product of f and g to be

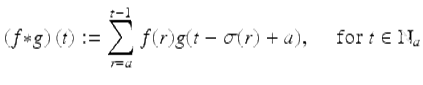
$$\displaystyle{ \left (f {\ast} g\right )\left (t\right ):=\sum \limits _{ r=a}^{t-1}f(r)g(t -\sigma (r) + a),\quad \mbox{ for $t \in \mathbb{N}_{ a}$} }$$

(2.42)

(note that $$\left (f {\ast} g\right )\left (a\right ) = 0$$ by our convention on sums).

Example 2.60.

For p ≠ 0, −1, find the convolution product e p (t, a) ∗ 1, and use your answer to find $$\mathcal{L}\{e_{p}(t,a) {\ast} 1\}(s).$$ By the definition of the convolution product

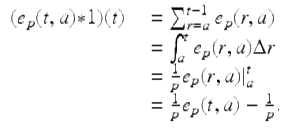
$$\displaystyle\begin{array}{rcl} (e_{p}(t,a) {\ast} 1)(t)& & =\sum _{ r=a}^{t-1}e_{ p}(r,a) {}\\ & & =\int _{ a}^{t}e_{ p}(r,a)\Delta r {}\\ & & = \frac{1} {p}e_{p}(r,a)\vert _{a}^{t} {}\\ & & = \frac{1} {p}e_{p}(t,a) -\frac{1} {p}. {}\\ \end{array}$$

It follows that

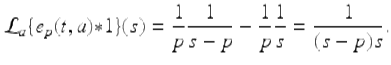
$$\displaystyle{\mathcal{L}_{a}\{e_{p}(t,a) {\ast} 1\}(s) = \frac{1} {p} \frac{1} {s - p} -\frac{1} {p} \frac{1} {s} = \frac{1} {(s - p)s}.}$$

Note from Example 2.60 we get that

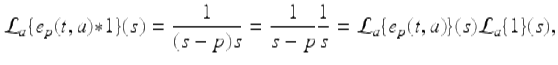
$$\displaystyle{\mathcal{L}_{a}\{e_{p}(t,a) {\ast} 1\}(s) = \frac{1} {(s - p)s} = \frac{1} {s - p} \frac{1} {s} = \mathcal{L}_{a}\{e_{p}(t,a)\}(s)\mathcal{L}_{a}\{1\}(s),}$$

which is a special case of the following theorem which gives a formula for the Laplace transform of the convolution product of two functions. Later we will show that this formula is useful in solving fractional initial value problems. In this theorem we use the notation $$F_{a}(s):= \mathcal{L}_{a}\{f\}(s),$$ which was introduced earlier.

Theorem 2.61 (Convolution Theorem).

Let $$f,g: \mathbb{N}_{a} \rightarrow \mathbb{R}$$ be of exponential order r 0 > 0. Then

$$\displaystyle{ \mathcal{L}_{a}\left \{f {\ast} g\right \}(s) = F_{a}(s)G_{a}(s),\quad \mbox{ for $\vert s + 1\vert > r_{0}$ }. }$$

(2.43)

Proof.

We have

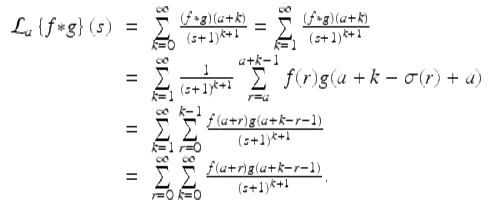
$$\displaystyle\begin{array}{rcl} \mathcal{L}_{a}\left \{f {\ast} g\right \}(s)& =& \sum \limits _{k=0}^{\infty }\frac{\left (f {\ast} g\right )(a + k)} {\left (s + 1\right )^{k+1}} =\sum \limits _{ k=1}^{\infty }\frac{\left (f {\ast} g\right )(a + k)} {\left (s + 1\right )^{k+1}} {}\\ & =& \sum \limits _{k=1}^{\infty } \frac{1} {\left (s + 1\right )^{k+1}}\sum \limits _{r=a}^{a+k-1}f(r)g(a + k -\sigma (r) + a) {}\\ & =& \sum \limits _{k=1}^{\infty }\sum \limits _{ r=0}^{k-1}\frac{f(a + r)g(a + k - r - 1)} {\left (s + 1\right )^{k+1}} {}\\ & =& \sum \limits _{r=0}^{\infty }\sum \limits _{ k=0}^{\infty }\frac{f(a + r)g(a + k - r - 1)} {\left (s + 1\right )^{k+1}}. {}\\ \end{array}$$

Making the change of variables $$\tau = k - r - 1$$ gives us that

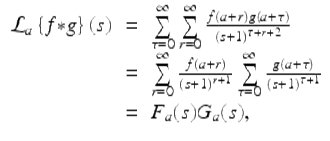
$$\displaystyle\begin{array}{rcl} \mathcal{L}_{a}\left \{f {\ast} g\right \}(s)& =& \sum \limits _{\tau =0}^{\infty }\sum \limits _{ r=0}^{\infty }\frac{f(a + r)g(a+\tau )} {\left (s + 1\right )^{\tau +r+2}} {}\\ & =& \sum \limits _{r=0}^{\infty } \frac{f(a + r)} {\left (s + 1\right )^{r+1}}\sum \limits _{\tau =0}^{\infty } \frac{g(a+\tau )} {\left (s + 1\right )^{\tau +1}} {}\\ & =& F_{a}(s)G_{a}(s), {}\\ \end{array}$$

for | s + 1 |  > r 0.  □ 

Example 2.62.

Solve the (Volterra) summation equation

$$\displaystyle{ y(t) = 3 + 12\sum _{r=0}^{t-1}\;\left [2^{t-r-1} - 1\right ]\;y(r),\quad t \in \mathbb{N}_{ 0} }$$

(2.44)

using Laplace transforms. We can write equation (2.44) in the equivalent form

$$\displaystyle\begin{array}{rcl} y(t)& =& 3 + 12\;\sum _{r=0}^{t-1}[e_{ 1}(t - r - 1,0) - 1]y(r) \\ & =& 3 + 12\;[(e_{1}(t,0) - 1) {\ast} y(t)],\quad t \in \mathbb{N}_{0}.{}\end{array}$$

(2.45)

Taking the Laplace transform (based at 0) of both sides of (2.45), we obtain

$$\displaystyle\begin{array}{rcl} Y _{0}(s)& =& \frac{3} {s} + 12\;\left [ \frac{1} {s - 1} -\frac{1} {s}\right ]\;Y _{0}(s) {}\\ & =& \frac{3} {s} + \frac{12} {s(s - 1)}Y _{0}(s). {}\\ \end{array}$$

Solving for Y 0(s), we get

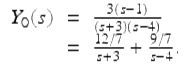
$$\displaystyle\begin{array}{rcl} Y _{0}(s)& =& \frac{3(s - 1)} {(s + 3)(s - 4)} {}\\ & =& \frac{12/7} {s + 3} + \frac{9/7} {s - 4}. {}\\ \end{array}$$

Taking the inverse Laplace transform of both sides, we get

$$\displaystyle\begin{array}{rcl} y(t)& =& \frac{12} {7} e_{-3}(t,0) + \frac{9} {7}e_{4}(t,0) {}\\ & =& \frac{12} {7} (-2)^{t} + \frac{9} {7}\;5^{t}. {}\\ \end{array}$$