The Laplace Transform of Fractional Operators - Discrete Delta Fractional Calculus and Laplace Transforms - Discrete Fractional Calculus

Discrete Fractional Calculus (2015)

2. Discrete Delta Fractional Calculus and Laplace Transforms

2.8. The Laplace Transform of Fractional Operators

With Corollary 2.66 in hand to insure the correct domain of convergence for the Laplace transform of any fractional operator, we may now safely develop formulas for applying the Laplace transform to fractional operators. This is the content of the next theorem.

Theorem 2.67.

Suppose $$f: \mathbb{N}_{a} \rightarrow \mathbb{R}$$ is of exponential order r ≥ 1, and let ν > 0 be given with N − 1 < ν ≤ N. Then for |s + 1| > r,

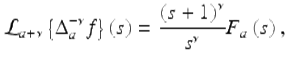
$$\displaystyle{ \mathcal{L}_{a+\nu }\left \{\Delta _{a}^{-\nu }f\right \}(s) = \frac{\left (s + 1\right )^{\nu }} {s^{\nu }} F_{a}\left (s\right ), }$$

(2.49)

and

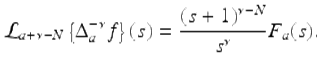
$$\displaystyle{ \mathcal{L}_{a+\nu -N}\left \{\Delta _{a}^{-\nu }f\right \}(s) = \frac{(s + 1)^{\nu -N}} {s^{\nu }} F_{a}(s). }$$

(2.50)

Proof.

Since $$f: \mathbb{N}_{a} \rightarrow \mathbb{R}$$ is of exponential order r ≥ 1, F a (s) exists for | s + 1 |  > r and by Corollary 2.66 both $$\mathcal{L}_{a+\nu }\left \{\Delta _{a}^{-\nu }f\right \}(s)$$ and $$\mathcal{L}_{a+\nu -N}\left \{\Delta _{a}^{-\nu }f\right \}(s)$$ exist for | s + 1 |  > r. First, we find a relationship between the left-hand sides of equations (2.49) and (2.50). Using (2.37), we get

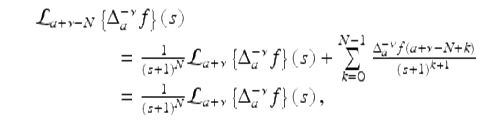
$$\displaystyle\begin{array}{rcl} & & \mathcal{L}_{a+\nu -N}\left \{\Delta _{a}^{-\nu }f\right \}\left (s\right ) \\ & & \quad \quad \quad \quad = \frac{1} {\left (s + 1\right )^{N}}\mathcal{L}_{a+\nu }\left \{\Delta _{a}^{-\nu }f\right \}\left (s\right ) +\sum \limits _{ k=0}^{N-1}\frac{\Delta _{a}^{-\nu }f\left (a +\nu -N + k\right )} {\left (s + 1\right )^{k+1}} \\ & & \quad \quad \quad \quad = \frac{1} {\left (s + 1\right )^{N}}\mathcal{L}_{a+\nu }\left \{\Delta _{a}^{-\nu }f\right \}\left (s\right ), {}\end{array}$$

(2.51)

using the fact that $$\Delta _{a}^{-\nu }f(a +\nu -N + k) = 0$$ for 0 ≤ k ≤ N − 1, by our convention on sums.

To see that (2.49) holds, note that

$$\displaystyle\begin{array}{rcl} & & \mathcal{L}_{a+\nu }\left \{\Delta _{a}^{-\nu }f\right \}(s) {}\\ & =& \sum \limits _{k=0}^{\infty }\frac{\Delta _{a}^{-\nu }f(a + k+\nu )} {(s + 1)^{k+1}} {}\\ & =& \sum \limits _{k=0}^{\infty } \frac{1} {(s + 1)^{k+1}}\sum _{r=a}^{k+a}h_{\nu -1}(a + k+\nu,\sigma (r))f(r) {}\\ & =& \sum \limits _{k=0}^{\infty } \frac{1} {(s + 1)^{k+1}}\sum _{r=a}^{k+a}f(r)h_{\nu -1}\left (\left (a + k + 1\right ) -\sigma (r) + a,a -\left (\nu -1\right )\right ) {}\\ & =& \sum \limits _{k=0}^{\infty }\frac{\left (f {\ast} h_{\nu -1}(t,a -\left (\nu -1)\right )\right )\left (a + 1 + k\right )} {(s + 1)^{k+1}},\quad \quad \quad \quad \text{ by (<InternalRef RefID="Equ119">2.42</InternalRef>)} {}\\ & =& \mathcal{L}_{a+1}\left \{f {\ast} h_{\nu -1}(t,a -\left (\nu -1)\right )\right \}\left (s\right ) {}\\ & =& \left (s + 1\right )\mathcal{L}_{a}\left \{f {\ast} h_{\nu -1}(t,a -\left (\nu -1)\right )\right \}\left (s\right ),\quad \text{ using (<InternalRef RefID="Equ110">2.38</InternalRef>) and (<InternalRef RefID="Equ119">2.42</InternalRef>)} {}\\ & =& \left (s + 1\right )F_{a}\left (s\right )\mathcal{L}_{a}\left \{h_{\nu -1}(t,a -\left (\nu -1)\right )\right \}\left (s\right ),\quad \quad \quad \quad \text{by (<InternalRef RefID="Equ121">2.43</InternalRef>)} {}\\ & =& \frac{\left (s + 1\right )^{\nu }} {s^{\nu }} F_{a}\left (s\right )\text{, applying (<InternalRef RefID="Equ110">2.38</InternalRef>), since }r \geq 1 {}\\ \end{array}$$

proving (2.49). Finally, using (2.51) and (2.49), we get

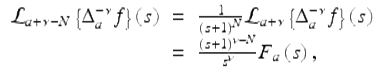
$$\displaystyle\begin{array}{rcl} \mathcal{L}_{a+\nu -N}\left \{\Delta _{a}^{-\nu }f\right \}(s)& =& \frac{1} {\left (s + 1\right )^{N}}\mathcal{L}_{a+\nu }\left \{\Delta _{a}^{-\nu }f\right \}\left (s\right ) {}\\ & =& \frac{\left (s + 1\right )^{\nu -N}} {s^{\nu }} F_{a}\left (s\right ), {}\\ \end{array}$$

for | s + 1 |  > r, proving (2.50). □ 

Example 2.68.

Find $$\mathcal{L}_{2+\pi +e}\{\Delta _{5+\pi }^{-e}f\}(s)$$ given that

$$\displaystyle{f(t) = (t - 5)^{\underline{\pi }},\quad t \in \mathbb{N}_{5+\pi }.}$$

First note that

$$\displaystyle{f(t) = \Gamma (\pi +1)h_{\pi }(t,5),\quad t \in \mathbb{N}_{5+\pi },}$$

and hence using (2.39) we have that

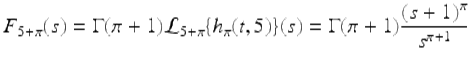
$$\displaystyle{F_{5+\pi }(s) = \Gamma (\pi +1)\mathcal{L}_{5+\pi }\{h_{\pi }(t,5)\}(s) = \Gamma (\pi +1)\frac{(s + 1)^{\pi }} {s^{\pi +1}} }$$

for | s + 1 |  > 1. 

Then using (2.50) gives us

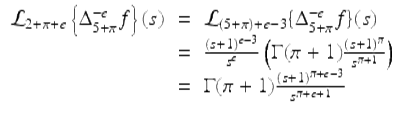
$$\displaystyle\begin{array}{rcl} \mathcal{L}_{2+\pi +e}\left \{\Delta _{5+\pi }^{-e}f\right \}(s)& =& \mathcal{L}_{ (5+\pi )+e-3}\{\Delta _{5+\pi }^{-e}f\}(s) {}\\ & =& \frac{\left (s + 1\right )^{e-3}} {s^{e}} \left (\Gamma (\pi +1)\frac{\left (s + 1\right )^{\pi }} {s^{\pi +1}} \right ) {}\\ & =& \Gamma (\pi +1)\frac{\left (s + 1\right )^{\pi +e-3}} {s^{\pi +e+1}} {}\\ \end{array}$$

for | s + 1 |  > 1. 

Remark 2.69.

Note that when ν = N in (2.50), the correct well-known formula (2.46) for N = 1, is obtained. This holds true for the Laplace transform of a fractional difference as well, as the following theorem shows (Holm [123]).

Theorem 2.70.

Suppose $$f: \mathbb{N}_{a} \rightarrow \mathbb{R}$$ is of exponential order r ≥ 1, and let ν > 0 be given with N − 1 < ν ≤ N. Then for |s + 1| > r

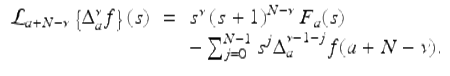
$$\displaystyle\begin{array}{rcl} \mathcal{L}_{a+N-\nu }\left \{\Delta _{a}^{\nu }f\right \}(s)& =& s^{\nu }\left (s + 1\right )^{N-\nu }F_{ a}(s) \\ & & -\sum _{j=0}^{N-1}s^{j}\Delta _{ a}^{\nu -1-j}f(a + N-\nu ).{}\end{array}$$

(2.52)

Proof.

Let f, r, ν, and N be given as in the statement of the theorem. By Exercise 2.28 we have that (2.52) holds when ν = N. Hence we assume N − 1 < ν < N. To see this, consider

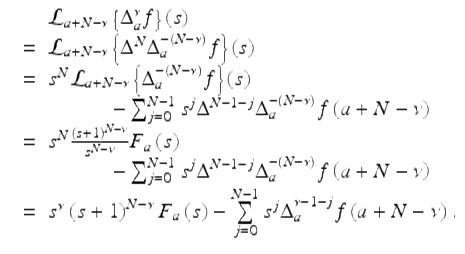
$$\displaystyle\begin{array}{rcl} & & \mathcal{L}_{a+N-\nu }\left \{\Delta _{a}^{\nu }f\right \}(s) {}\\ & =& \mathcal{L}_{a+N-\nu }\left \{\Delta ^{N}\Delta _{ a}^{-\left (N-\nu \right )}f\right \}(s) {}\\ & =& s^{N}\mathcal{L}_{ a+N-\nu }\left \{\Delta _{a}^{-\left (N-\nu \right )}f\right \}(s) {}\\ & \; & \quad \quad \quad -\sum _{j=0}^{N-1}s^{j}\Delta ^{N-1-j}\Delta _{ a}^{-(N-\nu )}f\left (a + N-\nu \right ) {}\\ & =& s^{N}\frac{\left (s + 1\right )^{N-\nu }} {s^{N-\nu }} F_{a}\left (s\right ) {}\\ & \; & \quad \quad \quad -\sum _{j=0}^{N-1}s^{j}\Delta ^{N-1-j}\Delta _{ a}^{-(N-\nu )}f\left (a + N-\nu \right ) {}\\ & =& s^{\nu }\left (s + 1\right )^{N-\nu }F_{ a}\left (s\right ) -\sum \limits _{j=0}^{N-1}s^{j}\Delta _{ a}^{\nu -1-j}f\left (a + N-\nu \right ). {}\\ \end{array}$$

This completes the proof. □