Power Rule and Composition Rule - Discrete Delta Fractional Calculus and Laplace Transforms

Discrete Fractional Calculus (2015)

2. Discrete Delta Fractional Calculus and Laplace Transforms

2.9. Power Rule and Composition Rule

In this section (see Atici and Eloe [34], Holm [123, 125]), we present a number of properties and formulas concerning fractional sum and difference operators are developed. These include composition rules and fractional power rules, whose proofs employ a variety of tools, none of which involves the Laplace transform. However, some of these results may also be proved using the Laplace transform. The following are two previously known results for which the Laplace transform provides a significantly shorter and cleaner proof than the original ones found in [34, 123].

Theorem 2.71 (Power Rule).

Let ν,μ > 0 be given. Then for $t \in \mathbb{N}_{a+\mu +\nu },$

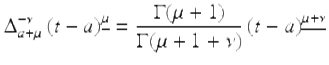
$\displaystyle{ \Delta _{a+\mu }^{-\nu }\left (t - a\right )^{\underline{\mu }} = \frac{\Gamma (\mu +1)} {\Gamma (\mu +1+\nu )}\left (t - a\right )^{\underline{\mu +\nu }} }$

or equivalently

$\displaystyle{ \Delta _{a+\mu }^{-\nu }h_{\mu }(t,a) = h_{\mu +\nu }(t,a). }$

Proof.

Applying Remark 2.57 together with Lemma 2.63, we conclude that for each ε > 0, $\left (t - a\right )^{\underline{\mu }}$ is of exponential order 1 +ε and therefore we have that $\Delta _{a+\mu }^{-\nu }\left (t - a\right )^{\underline{\mu }}$ is of exponential order 1 + 2ε. Thus, after employing an argument similar to that given in Corollary 2.66, we conclude that both $\mathcal{L}_{a+\mu }\left \{\left (t - a\right )^{\underline{\mu }}\right \}$ and $\mathcal{L}_{a+\mu +\nu }\left \{\Delta _{a+\mu }^{-\nu }\left (t - a\right )^{\underline{\mu }}\right \}$ converge for | s + 1 | > 1. Hence, for | s + 1 | > 1, we have

$\displaystyle\begin{array}{rcl} & & \mathcal{L}_{a+\mu +\nu }\left \{\Delta _{a+\mu }^{-\nu }\left (t - a\right )^{\underline{\mu }}\right \}\left (s\right ) {}\\ & & \quad \quad \quad \quad = \frac{\left (s + 1\right )^{\nu }} {s^{\nu }} \mathcal{L}_{a+\mu }\left \{\left (t - a\right )^{\underline{\mu }}\right \}\left (s\right ),\quad \text{ using (<InternalRef RefID="Equ136">2.49</InternalRef>)} {}\\ & & \quad \quad \quad \quad = \frac{\left (s + 1\right )^{\nu }} {s^{\nu }} \Gamma (\mu +1)\mathcal{L}_{a+\mu }\left \{h_{\mu }\left (t,a\right )\right \}\left (s\right ) {}\\ & & \quad \quad \quad \quad = \frac{\left (s + 1\right )^{\nu }} {s^{\nu }} \Gamma (\mu +1)\frac{\left (s + 1\right )^{\mu }} {s^{\mu +1}},\quad \text{ applying (<InternalRef RefID="Equ114">2.39</InternalRef>)} {}\\ & & \quad \quad \quad \quad = \Gamma (\mu +1)\frac{\left (s + 1\right )^{\mu +\nu }} {s^{\mu +\nu +1}} {}\\ & & \quad \quad \quad \quad = \Gamma (\mu +1)\mathcal{L}_{a+\mu +\nu }\left \{h_{\mu +\nu }\left (t,a\right )\right \}\left (s\right ) {}\\ & & \quad \quad \quad \quad = \mathcal{L}_{a+\mu +\nu }\left \{ \frac{\Gamma (\mu +1)} {\Gamma (\mu +\nu + 1)}\left (t - a\right )^{\underline{\mu +\nu }}\right \}\left (s\right ). {}\\ \end{array}$

Since the Laplace transform is injective, it follows that

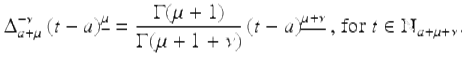
$\displaystyle{ \Delta _{a+\mu }^{-\nu }\left (t - a\right )^{\underline{\mu }} = \frac{\Gamma (\mu +1)} {\Gamma (\mu +1+\nu )}\left (t - a\right )^{\underline{\mu +\nu }}\text{, for }t \in \mathbb{N}_{ a+\mu +\nu }. }$

This completes the proof. □

Theorem 2.72.

Suppose that $f: \mathbb{N}_{a} \rightarrow \mathbb{R}$ is of exponential order r ≥ 1, and let ν,μ > 0 be given. Then

$\displaystyle{ \Delta _{a+\mu }^{-\nu }\Delta _{ a}^{-\mu }f(t) = \Delta _{ a}^{-\nu -\mu }f(t) = \Delta _{ a+\nu }^{-\mu }\Delta _{ a}^{-\nu }f(t),\text{ for all }t \in \mathbb{N}_{ a+\mu +\nu }. }$

Proof.

Let f, r, ν, and μ be given as in the statement of the theorem. It follows from Corollary 2.66 that each of

$\displaystyle{ \mathcal{L}_{a+\mu +\nu }\left \{\Delta _{a+\mu }^{-\nu }\Delta _{ a}^{-\mu }f\right \},\mathcal{L}_{ a+\mu }\left \{\Delta _{a}^{-\mu }f\right \}\text{ and }\mathcal{L}_{ a+\left (\nu +\mu \right )}\left \{\Delta _{a}^{-(\nu +\mu )}f\right \} }$

exists for | s + 1 | > r. Therefore, we may apply (2.49) multiple times to write for | s + 1 | > r,

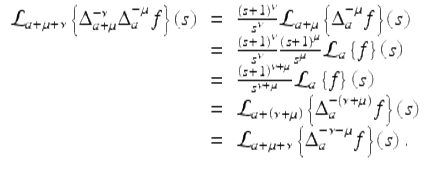
$\displaystyle\begin{array}{rcl} \mathcal{L}_{a+\mu +\nu }\left \{\Delta _{a+\mu }^{-\nu }\Delta _{ a}^{-\mu }f\right \}\left (s\right )& =& \frac{\left (s + 1\right )^{\nu }} {s^{\nu }} \mathcal{L}_{a+\mu }\left \{\Delta _{a}^{-\mu }f\right \}\left (s\right ) {}\\ & =& \frac{\left (s + 1\right )^{\nu }} {s^{\nu }} \frac{\left (s + 1\right )^{\mu }} {s^{\mu }} \mathcal{L}_{a}\left \{f\right \}\left (s\right ) {}\\ & =& \frac{\left (s + 1\right )^{\nu +\mu }} {s^{\nu +\mu }} \mathcal{L}_{a}\left \{f\right \}\left (s\right ) {}\\ & =& \mathcal{L}_{a+\left (\nu +\mu \right )}\left \{\Delta _{a}^{-(\nu +\mu )}f\right \}\left (s\right ) {}\\ & =& \mathcal{L}_{a+\mu +\nu }\left \{\Delta _{a}^{-\nu -\mu }f\right \}\left (s\right ). {}\\ \end{array}$

The result follows from symmetry and the fact that the operator $\mathcal{L}_{a+\mu +\nu }$ is injective (see Theorem 2.7). □