The Laplace Transform Method - Discrete Delta Fractional Calculus and Laplace Transforms

Discrete Fractional Calculus (2015)

2. Discrete Delta Fractional Calculus and Laplace Transforms

2.10. The Laplace Transform Method

The tools developed in the previous sections of this chapter enable us to solve a general fractional initial value problem using the Laplace transform. The initial value problem (2.53) below is identical to that studied and solved using the composition rules in Holm [123, 125]. In Theorem 2.76 below, we present only that part of the proof involving the Laplace transform method.

Theorem 2.73.

Assume $f: \mathbb{N}_{a} \rightarrow \mathbb{R}$ is of exponential order r ≥ 1 and ν > 0 with N − 1 < ν ≤ N. Then the unique solution of the IVP

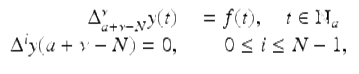
$\displaystyle\begin{array}{rcl} \Delta _{a+\nu -N}^{\nu }y(t)& & = f(t),\quad t \in \mathbb{N}_{ a} {}\\ \Delta ^{i}y(a +\nu -N) = 0,& & \quad 0 \leq i \leq N - 1, {}\\ \end{array}$

is given by

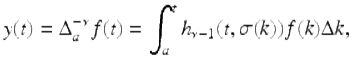
$\displaystyle{y(t) = \Delta _{a}^{-\nu }f(t) =\int _{ a}^{t}h_{\nu -1}(t,\sigma (k))f(k)\Delta k,}$

for $t \in \mathbb{N}_{a+\nu -N}.$

Proof.

Since

$\displaystyle{\Delta _{a+\nu -N}^{\nu }y(t) = f(t),\quad t \in \mathbb{N}_{ a},}$

we have that

$\displaystyle{\mathcal{L}_{a}\{\Delta _{a+\nu -N}^{\nu }y\}(s) = F_{ a}(s)}$

for | s + 1 | > r. Assume for the moment that the Laplace transform (based at $a +\nu -N$ ) of the solution of the given IVP converges for | s + 1 | > r. It follows from (2.52) that

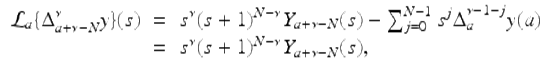
$\displaystyle\begin{array}{rcl} \mathcal{L}_{a}\{\Delta _{a+\nu -N}^{\nu }y\}(s)& =& s^{\nu }(s + 1)^{N-\nu }Y _{ a+\nu -N}(s) -\sum _{j=0}^{N-1}s^{j}\Delta _{ a}^{\nu -1-j}y(a) {}\\ & =& s^{\nu }(s + 1)^{N-\nu }Y _{ a+\nu -N}(s), {}\\ \end{array}$

where we have used the initial conditions. It follows that

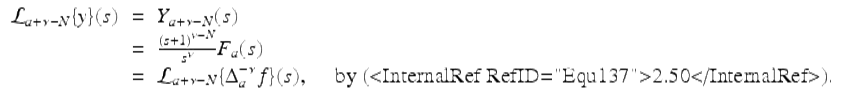
$\displaystyle\begin{array}{rcl} \mathcal{L}_{a+\nu -N}\{y\}(s)& =& Y _{a+\nu -N}(s) {}\\ & =& \frac{(s + 1)^{\nu -N}} {s^{\nu }} F_{a}(s) {}\\ & =& \mathcal{L}_{a+\nu -N}\{\Delta _{a}^{-\nu }f\}(s),\quad \mbox{ by (<InternalRef RefID="Equ137">2.50</InternalRef>)}. {}\\ \end{array}$

It then follows from the uniqueness theorem for Laplace transforms, Theorem 2.7, that

$\displaystyle{y(t) = \Delta _{a}^{-\nu }f(t),\quad t \in \mathbb{N}_{ a+\nu -N}.}$

From this we now know that y is of exponential order r and hence the above arguments hold and the proof is complete. □

Using Theorem 2.73 and Theorem 2.43 it is easy to prove the following result.

Theorem 2.74.

Assume $f: \mathbb{N}_{a} \rightarrow \mathbb{R}$ is of exponential order r ≥ 1 and ν > 0 with N − 1 < ν ≤ N. Then a general solution of the nonhomogeneous equation

$\displaystyle{ \Delta _{a+\nu -N}^{\nu }y(t) = f(t),\quad t \in \mathbb{N}_{ a} }$

is given by

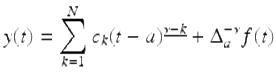
$\displaystyle{y(t) =\sum _{ k=1}^{N}c_{ k}(t - a)^{\underline{\nu -k}} + \Delta _{ a}^{-\nu }f(t)}$

for $t \in \mathbb{N}_{a+\nu -N}.$

Example 2.75.

Solve the IVP

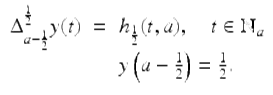
$\displaystyle\begin{array}{rcl} \Delta _{a-\frac{1} {2} }^{ \frac{1} {2} }y(t)& =& h_{\frac{1} {2} }(t,a),\quad t \in \mathbb{N}_{a} {}\\ & & y\left (a -\frac{1} {2}\right ) = \frac{1} {2}. {}\\ \end{array}$

Note this IVP is of the form of the IVP in Theorem 2.74, where

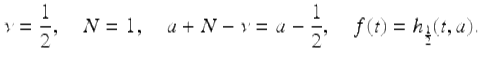
$\displaystyle{\nu = \frac{1} {2},\quad N = 1,\quad a + N-\nu = a -\frac{1} {2},\quad f(t) = h_{\frac{1} {2} }(t,a).}$

From Theorem 2.74 a general solution of the fractional equation 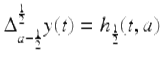$\Delta _{a-\frac{1} {2} }^{ \frac{1} {2} }y(t) = h_{\frac{1} {2} }(t,a)$ is given by

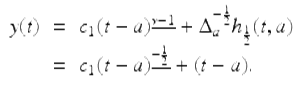
$\displaystyle\begin{array}{rcl} y(t)& =& c_{1}(t - a)^{\underline{\nu -1}} + \Delta _{ a}^{-\frac{1} {2} }h_{\frac{1} {2} }(t,a) {}\\ & =& c_{1}(t - a)^{\underline{-\frac{1} {2} }} + (t - a). {}\\ \end{array}$

Applying the initial condition we get $c_{1} = \frac{1} {\sqrt{\pi }}.$ Hence the solution of the given IVP in this example is given by

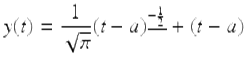
$\displaystyle{y(t) = \frac{1} {\sqrt{\pi }}(t - a)^{\underline{-\frac{1} {2} }} + (t - a)}$

for $t \in \mathbb{N}_{a-\frac{1} {2} }.$

The following theorem appears in Ahrendt et al. [3].

Theorem 2.76.

Suppose that $f: \mathbb{N}_{a} \rightarrow \mathbb{R}$ is of exponential order r ≥ 1, and let ν > 0 be given with N − 1 < ν ≤ N. The unique solution to the fractional initial value problem

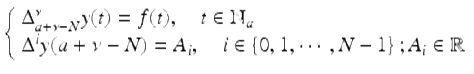
$\displaystyle{ \left \{\begin{array}{l} \Delta _{a+\nu -N}^{\nu }y(t) = f(t),\quad t \in \mathbb{N}_{a}\text{ } \\ \Delta ^{i}y(a +\nu -N) = A_{i},\quad i \in \left \{0,1,\cdots \,,N - 1\right \};A_{i} \in \mathbb{R}\end{array} \right. }$

(2.53)

is given by

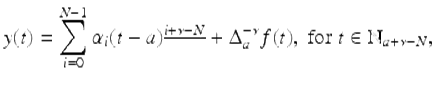
$\displaystyle{ y(t) =\sum \limits _{ i=0}^{N-1}\alpha _{ i}(t - a)^{\underline{i+\nu -N}} + \Delta _{ a}^{-\nu }f(t),\text{ for }t \in \mathbb{N}_{ a+\nu -N}, }$

where

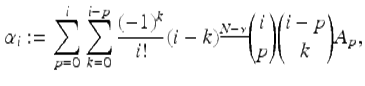
$\displaystyle{ \alpha _{i}:=\sum \limits _{ p=0}^{i}\sum \limits _{ k=0}^{i-p}\frac{(-1)^{k}} {i!} (i - k)^{\underline{N-\nu }}\binom{i}{p}\binom{i - p}{k}A_{ p}, }$

for $i \in \left \{0,1,\cdots \,,N - 1\right \}.$

Proof.

Since f is of exponential order r, we know that $F_{a}(s) = \mathcal{L}_{a}\left \{f\right \}(s)$ exists for | s + 1 | > r. So, applying the Laplace transform to both sides of the difference equation in (2.53), we have for | s + 1 | > r

$\displaystyle{ \mathcal{L}_{a}\left \{\Delta _{a+\nu -N}^{\nu }y\right \}(s) = F_{ a}(s). }$

Using (2.52), we get

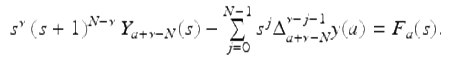
$\displaystyle\begin{array}{rcl} s^{\nu }\left (s + 1\right )^{N-\nu }Y _{ a+\nu -N}(s) -\sum \limits _{j=0}^{N-1}s^{j}\Delta _{ a+\nu -N}^{\nu -j-1}y(a) = F_{ a}(s).& & {}\\ \end{array}$

This implies that

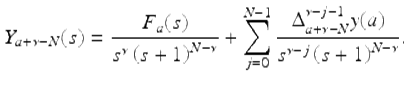
$\displaystyle{Y _{a+\nu -N}(s) = \frac{F_{a}(s)} {s^{\nu }\left (s + 1\right )^{N-\nu }} +\sum \limits _{ j=0}^{N-1}\frac{\Delta _{a+\nu -N}^{\nu -j-1}y(a)} {s^{\nu -j}\left (s + 1\right )^{N-\nu }}.}$

From (2.50), we have immediately that

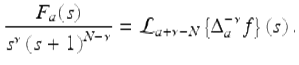
$\displaystyle{ \frac{F_{a}(s)} {s^{\nu }\left (s + 1\right )^{N-\nu }} = \mathcal{L}_{a+\nu -N}\left \{\Delta _{a}^{-\nu }f\right \}\left (s\right ). }$

Considering next the terms in the summation, we have for each fixed j ∈ { 0, ⋯ , N − 1},

$\displaystyle\begin{array}{rcl} & & \frac{1} {s^{\nu -j}\left (s + 1\right )^{N-\nu }} = \frac{1} {\left (s + 1\right )^{N-j-1}} \frac{\left (s + 1\right )^{\nu -j-1}} {s^{\nu -j}} {}\\ & & = \frac{1} {\left (s + 1\right )^{N-j-1}}\mathcal{L}_{a+\nu -j-1}\left \{h_{\nu -j-1}\left (t,a\right )\right \}(s),\quad \quad \quad \quad \quad \quad \;\;\text{ by (<InternalRef RefID="Equ114">2.39</InternalRef>)} {}\\ & & = \mathcal{L}_{a+\nu -N}\left \{h_{\nu -j-1}\left (t,a\right )\right \}(s) {}\\ & & -\sum \limits _{k=0}^{N-j-2}\frac{h_{\nu -j-1}\left (k + a +\nu -N,a\right )} {\left (s + 1\right )^{k+1}},\text{by (<InternalRef RefID="Equ109">2.37</InternalRef>)} {}\\ & & = \mathcal{L}_{a+\nu -N}\left \{h_{\nu -j-1}\left (t,a\right )\right \}(s), {}\\ \end{array}$

since

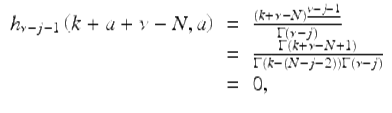
$\displaystyle\begin{array}{rcl} h_{\nu -j-1}\left (k + a +\nu -N,a\right )& =& \frac{\left (k +\nu -N\right )^{\underline{\nu -j-1}}} {\Gamma (\nu -j)} {}\\ & =& \frac{\Gamma (k +\nu -N + 1)} {\Gamma (k -\left (N - j - 2)\right )\Gamma (\nu -j)} {}\\ & =& 0, {}\\ \end{array}$

for $k \in \left \{0,\cdots \,,N - j - 2\right \}.$ It follows that for | s + 1 | > r,

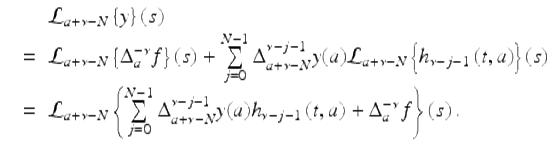
$\displaystyle\begin{array}{rcl} & & \mathcal{L}_{a+\nu -N}\left \{y\right \}(s) {}\\ & =& \mathcal{L}_{a+\nu -N}\left \{\Delta _{a}^{-\nu }f\right \}\left (s\right ) +\sum \limits _{ j=0}^{N-1}\Delta _{ a+\nu -N}^{\nu -j-1}y(a)\mathcal{L}_{ a+\nu -N}\left \{h_{\nu -j-1}\left (t,a\right )\right \}(s) {}\\ & =& \mathcal{L}_{a+\nu -N}\left \{\sum \limits _{j=0}^{N-1}\Delta _{ a+\nu -N}^{\nu -j-1}y(a)h_{\nu -j-1}\left (t,a\right ) + \Delta _{a}^{-\nu }f\right \}\left (s\right ). {}\\ \end{array}$

Since the Laplace transform is injective, we conclude that for $t \in \mathbb{N}_{a+\nu -N},$

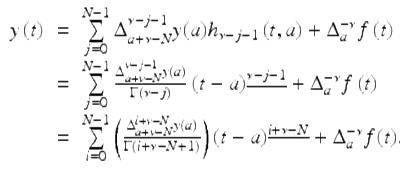
$\displaystyle\begin{array}{rcl} y\left (t\right )& =& \sum \limits _{j=0}^{N-1}\Delta _{ a+\nu -N}^{\nu -j-1}y(a)h_{\nu -j-1}\left (t,a\right ) + \Delta _{a}^{-\nu }f\left (t\right ) {}\\ & =& \sum \limits _{j=0}^{N-1}\frac{\Delta _{a+\nu -N}^{\nu -j-1}y(a)} {\Gamma (\nu -j)} \left (t - a\right )^{\underline{\nu -j-1}} + \Delta _{ a}^{-\nu }f\left (t\right ) {}\\ & =& \sum \limits _{i=0}^{N-1}\left (\frac{\Delta _{a+\nu -N}^{i+\nu -N}y(a)} {\Gamma (i +\nu -N + 1)} \right )\left (t - a\right )^{\underline{i+\nu -N}} + \Delta _{ a}^{-\nu }f(t). {}\\ \end{array}$

Moreover, Holm [125] showed that

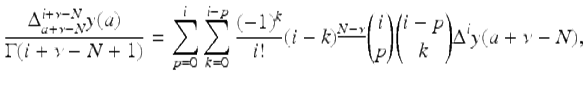
$\displaystyle{ \frac{\Delta _{a+\nu -N}^{i+\nu -N}y(a)} {\Gamma (i +\nu -N + 1)} =\sum \limits _{ p=0}^{i}\sum \limits _{ k=0}^{i-p}\frac{(-1)^{k}} {i!} (i - k)^{\underline{N-\nu }}\binom{i}{p}\binom{i - p}{k}\Delta ^{i}y(a +\nu -N), }$

for $i \in \left \{0,1,\cdots \,,N - 1\right \},$ concluding the proof. □

Theorem 2.76 shows how we can solve the general IVP (2.53) using the discrete Laplace transform method. We offer a brief example.

Example 2.77.

Consider the IVP given by

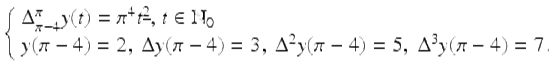
$\displaystyle{ \left \{\begin{array}{l} \Delta _{\pi -4}^{\pi }y(t) =\pi ^{4}t^{\underline{2}}\text{, }t \in \mathbb{N}_{0} \\ y(\pi -4) = 2,\text{ }\Delta y(\pi -4) = 3,\text{ }\Delta ^{2}y(\pi -4) = 5,\text{ }\Delta ^{3}y(\pi -4) = 7. \end{array} \right. }$

(2.54)

Note that (2.54) is a specific case of (2.53) from Theorem 2.76, with

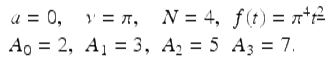
$\displaystyle{ \begin{array}{llll} a = 0, &\nu =\pi, &N = 4,&f(t) =\pi ^{4}t^{\underline{2}} \\ A_{0} = 2,&A_{1} = 3,&A_{2} = 5&A_{3} = 7.\end{array} }$

After applying the discrete Laplace transform method as described in Theorem 2.76, we have

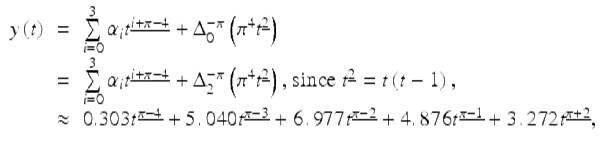
$\displaystyle\begin{array}{rcl} y\left (t\right )& =& \sum \limits _{i=0}^{3}\alpha _{ i}t^{\underline{i+\pi -4}} + \Delta _{ 0}^{-\pi }\left (\pi ^{4}t^{\underline{2}}\right ) {}\\ & =& \sum \limits _{i=0}^{3}\alpha _{ i}t^{\underline{i+\pi -4}} + \Delta _{ 2}^{-\pi }\left (\pi ^{4}t^{\underline{2}}\right )\text{, since }t^{\underline{2}} = t\left (t - 1\right ), {}\\ & \approx & 0.303t^{\underline{\pi -4}} + 5.\,040t^{\underline{\pi -3}} + 6.\,977t^{\underline{\pi -2}} + 4.\,876t^{\underline{\pi -1}} + 3.\,272t^{\underline{\pi +2}}, {}\\ \end{array}$

where in this last step, we calculated

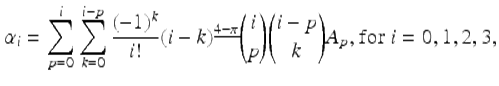
$\displaystyle{ \alpha _{i} =\sum \limits _{ p=0}^{i}\sum \limits _{ k=0}^{i-p}\frac{(-1)^{k}} {i!} (i - k)^{\underline{4-\pi }}\binom{i}{p}\binom{i - p}{k}A_{ p}\text{, for }i = 0,1,2,3\text{,} }$

for the first four terms and applied the power rule (Theorem 2.71) on the last term.