Preliminary Definitions - Nabla Fractional Calculus - Discrete Fractional Calculus

Discrete Fractional Calculus (2015)

3. Nabla Fractional Calculus

3.2. Preliminary Definitions

We first introduce some notation and state elementary results concerning the nabla calculus, which we will use in this chapter. As in Chaps. 1 and 2 for $$a \in \mathbb{R}$$ , the sets $$\mathbb{N}_{a}$$ and $$\mathbb{N}_{a}^{b}$$ , where b − a is a positive integer, are defined by

$$\displaystyle{\mathbb{N}_{a}:=\{ a,a + 1,a + 2,\ldots \},\quad \mathbb{N}_{a}^{b}:=\{ a,a + 1,a + 2,\ldots,b\}.}$$

For an arbitrary function $$f: \mathbb{N}_{a} \rightarrow \mathbb{R}$$ we define the nabla operator (backwards difference operator) , ∇, by

$$\displaystyle{(\nabla f)(t):= f(t) - f(t - 1),\quad t \in \mathbb{N}_{a+1}.}$$

For convenience, we adopt the convention that ∇f(t): = (∇f)(t). Sometimes it is useful to use the relation

$$\displaystyle{ \nabla f(t) = \Delta f(t - 1) }$$

(3.1)

to get results for the nabla calculus from the delta calculus and vice versa. Since many readers will be interested only in the nabla calculus, we want this chapter to be self-contained. So we will not use the formula (3.1) in this chapter. The operator ∇ n is defined recursively by $$\nabla ^{n}f(t):= \nabla \big(\nabla ^{n-1}f(t)\big)$$ for $$t \in \mathbb{N}_{a+n}$$ , $$n \in \mathbb{N}_{1}$$ , where ∇0 is the identity operator defined by ∇0 f(t) = f(t). We define the backward jump operator, $$\rho: \mathbb{N}_{a+1} \rightarrow \mathbb{N}_{a}$$ , by

$$\displaystyle{\rho (t) = t - 1.}$$

Also we let f ρ denote the composition function f ∘ρ. It is easy (Exercise 3.1) to see that if $$f: \mathbb{N} \rightarrow \mathbb{R}$$ and ∇f(t) = 0 for $$t \in \mathbb{N}_{a+1},$$ then

$$\displaystyle{f(t) = C,\quad t \in \mathbb{N}_{a},\quad \mbox{ where $C$ is a constant.}}$$

The following theorem gives several properties of the nabla difference operator.

Theorem 3.1.

Assume $$f,g: \mathbb{N}_{a} \rightarrow \mathbb{R}$$ and $$\alpha,\beta \in \mathbb{R}$$ . Then for $$t \in \mathbb{N}_{a+1},$$

(i)

∇α = 0;

(ii)

∇αf(t) = α∇f(t);

(iii)

$$\nabla \left (f(t) + g(t)\right ) = \nabla f(t) + \nabla g(t);$$

(iv)

if α ≠ 0, then $$\nabla \alpha ^{t+\beta } = \frac{\alpha -1} {\alpha } \alpha ^{t+\beta };$$

(v)

$$\nabla \left (f(t)g(t)\right ) = f(\rho (t))\nabla g(t) + \nabla f(t)g(t);$$

(vi)

$$\nabla \left (\frac{f(t)} {g(t)} \right ) = \frac{g(t)\nabla f(t)-f(t)\nabla g(t)} {g(t)g(\rho (t))},\quad \mbox{ if}\;\;g(t)\neq 0,\quad t \in \mathbb{N}_{a+1}$$ .

Proof.

We will just prove (iv) and (v) and leave the proof of the other parts to the reader. To see that (iv) holds assume that α ≠ 0 and note that

$$\displaystyle\begin{array}{rcl} \nabla \alpha ^{t+\beta }& =& \alpha ^{t+\beta } -\alpha ^{t-1+\beta } {}\\ & =& [\alpha -1]\alpha ^{t-1+\beta } {}\\ & =& \frac{\alpha -1} {\alpha } \alpha ^{t+\beta }. {}\\ \end{array}$$

Next we prove the product rule (v). For $$t \in \mathbb{N}_{a+1}$$ , consider

$$\displaystyle\begin{array}{rcl} \nabla [f(t)g(t)]& =& f(t)g(t) - f(t - 1)g(t - 1) {}\\ & =& f(t - 1)[g(t) - g(t - 1)] + [f(t) - f(t - 1)]g(t) {}\\ & =& f(\rho (t))\nabla g(t) + \nabla f(t)g(t), {}\\ \end{array}$$

which is the desired result. □ 

Next we define the rising function.

Definition 3.2.

Assume n is a positive integer and $$t \in \mathbb{R}$$ . Then we define the rising function, $$t^{\overline{n}},$$ read “t to the n rising,”by

$$\displaystyle{t^{\overline{n}}:= t(t + 1)\cdots (t + n - 1).}$$

Readers familiar with the Pochhammer function may recognize this notation in its alternative form, (k) n . See Knuth [139].

The rising function is defined this way so that the following power rule holds.

Theorem 3.3 (Nabla Power Rule).

For $$n \in \mathbb{N}_{1}$$ , $$\alpha \in \mathbb{R}$$ ,

$$\displaystyle{\nabla (t+\alpha )^{\overline{n}} = n\;(t+\alpha )^{\overline{n - 1}},}$$

for $$t \in \mathbb{R}$$ .

Proof.

We simply write

$$\displaystyle\begin{array}{rcl} \nabla (t+\alpha )^{\overline{n}}& =& (t+\alpha )^{\overline{n}} - (t - 1+\alpha )^{\overline{n}} {}\\ & =& [(t+\alpha )(t +\alpha +1)\cdots (t +\alpha +n - 1)] {}\\ & \quad -& [(t +\alpha -1)(t+\alpha )\cdots (t +\alpha +n - 2)] {}\\ & =& (t+\alpha )(t +\alpha +1)\cdots (t +\alpha +n - 2) {}\\ & \quad \cdot & [(t +\alpha +n - 1) - (t +\alpha -1)] {}\\ & =& n\;(t+\alpha )^{\overline{n - 1}}. {}\\ \end{array}$$

This completes the proof. □ 

Note that for $$n \in \mathbb{N}_{1}$$ ,

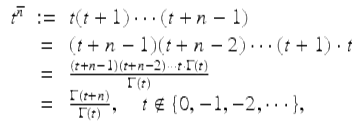
$$\displaystyle\begin{array}{rcl} t^{\overline{n}}&:=& t(t + 1)\cdots (t + n - 1) {}\\ & =& (t + n - 1)(t + n - 2)\cdots (t + 1) \cdot t {}\\ & =& \frac{(t + n - 1)(t + n - 2)\cdots t \cdot \Gamma (t)} {\Gamma (t)} {}\\ & =& \frac{\Gamma (t + n)} {\Gamma (t)},\quad t\notin \{0,-1,-2,\cdots \,\}, {}\\ \end{array}$$

where $$\Gamma $$ is the gamma function (Definition 1.6). Motivated by this we next define the (generalized) rising function as follows.

Definition 3.4.

The (generalized) rising function is defined by

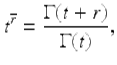
$$\displaystyle{ t^{\overline{r}} = \frac{\Gamma (t + r)} {\Gamma (t)}, }$$

(3.2)

for those values of t and r so that the right-hand side of equation (3.2) is sensible. Also, we use the convention that if t is a nonpositive integer, but t + r is not a nonpositive integer, then $$t^{\overline{r}}:= 0$$ .

We then get the following generalized power rules.

Theorem 3.5 (Generalized Nabla Power Rules).

The formulas

$$\displaystyle{ \nabla (t+\alpha )^{\overline{r}} = r\;(t+\alpha )^{\overline{r - 1}}, }$$

(3.3)

and

$$\displaystyle{ \nabla (\alpha -t)^{\overline{r}} = -r(\alpha -\rho (t))^{\overline{r - 1}}, }$$

(3.4)

hold for those values of t, r, and α so that the expressions in equations (3.3) and (3.4) are sensible. In particular, $$t^{\overline{0}} = 1,$$ $$t\neq 0,-1,-2,\cdots $$ .

Proof.

Consider that

$$\displaystyle\begin{array}{rcl} \nabla (t+\alpha )^{\overline{r}}& =& (t+\alpha )^{\overline{r}} - (t - 1+\alpha )^{\overline{r}} {}\\ & =& \frac{\Gamma (t +\alpha +r)} {\Gamma (t+\alpha )} -\frac{\Gamma (t +\alpha +r - 1)} {\Gamma (t +\alpha -1)} {}\\ & =& [(t +\alpha +r - 1) - (t +\alpha -1)]\frac{\Gamma (t +\alpha +r - 1)} {\Gamma (t+\alpha )} {}\\ & =& r\frac{\Gamma (t +\alpha +r - 1)} {\Gamma (t+\alpha )} {}\\ & =& r(t+\alpha )^{\overline{r - 1}}. {}\\ \end{array}$$

Hence, (3.3) holds. Next we prove (3.4). To see this, note that

$$\displaystyle\begin{array}{rcl} \nabla (\alpha -t)^{\overline{r}}& =& (\alpha -t)^{\overline{r}} - (\alpha -t + 1)^{\overline{r}} {}\\ & =& \frac{\Gamma (\alpha -t + r)} {\Gamma (\alpha -t)} -\frac{\Gamma (\alpha -t + 1 + r)} {\Gamma (\alpha -t + 1)} {}\\ & =& [(\alpha -t) - (\alpha -t + r)]\frac{\Gamma (\alpha -t + r)} {\Gamma (\alpha -t + 1)} {}\\ & =& -\,r\ \frac{\Gamma (\alpha -t + r)} {\Gamma (\alpha -t + 1)} {}\\ & =& -\,r\ \frac{\Gamma (\alpha -\rho (t) + r - 1)} {\Gamma (\alpha -\rho (t))} {}\\ & =& -\,r(\alpha -\rho (t))^{\overline{r - 1}}. {}\\ \end{array}$$

This completes the proof. □