Nabla Exponential Function - Nabla Fractional Calculus - Discrete Fractional Calculus

Discrete Fractional Calculus (2015)

3. Nabla Fractional Calculus

3.3. Nabla Exponential Function

In this section we want to study the nabla exponential function that plays a similar role in the nabla calculus that the exponential function e pt does in the continuous calculus. Motivated by the fact that when p is a constant, x(t) = e ptis the unique solution of the initial value problem

$$\displaystyle{x' = px,\quad x(0) = 1,}$$

we define the nabla exponential function, E p (t, s) based at $$s \in \mathbb{N}_{a}$$ , where the function p is in the set of (nabla) regressive functions

$$\displaystyle{\mathcal{R}:=\{ p: \mathbb{N}_{a+1} \rightarrow \mathbb{R}: \quad 1 - p(t)\neq 0,\quad \mbox{ for}\quad t \in \mathbb{N}_{a+1}\},}$$

to be the unique solution of the initial value problem

$$\displaystyle{ \nabla y(t) = p(t)y(t),\quad t \in \mathbb{N}_{a+1} }$$

(3.5)

$$\displaystyle{ y(s) = 1. }$$

(3.6)

After reading the proof of the next theorem one sees why this IVP has a unique solution. In the next theorem we give a formula for the exponential function E p (t, s).

Theorem 3.6.

Assume $$p \in \mathcal{R}$$ and $$s \in \mathbb{N}_{a}$$ . Then

$$\displaystyle{ E_{p}(t,s) = \left \{\begin{array}{@{}l@{\quad }l@{}} \prod _{\tau =s+1}^{t} \frac{1} {1-p(\tau )}\text{, } \quad &t \in \mathbb{N}_{s} \\ \prod _{\tau =t+1}^{s}[1 - p(\tau )]\text{, }\quad &t \in \mathbb{N}_{a}^{s-1}. \end{array} \right. }$$

(3.7)

Here it is understood that $$\prod _{\tau =t+1}^{t}h(\tau ) = 1$$ for any function h.

Proof.

First we find a formula for E p (t, s) for t ≥ s + 1 by solving the IVP (3.5), (3.6) by iteration. Solving the nabla difference equation (3.5) for y(t) we obtain

$$\displaystyle\begin{array}{rcl} y(t) = \frac{1} {1 - p(t)}y(t - 1),\quad t \in \mathbb{N}_{a+1}.& &{}\end{array}$$

(3.8)

Letting $$t = s + 1$$ in (3.8) we get

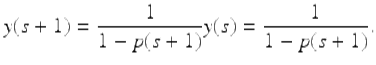
$$\displaystyle{y(s + 1) = \frac{1} {1 - p(s + 1)}y(s) = \frac{1} {1 - p(s + 1)}.}$$

Then letting $$t = s + 2$$ in (3.8) we obtain

$$\displaystyle{y(s + 2) = \frac{1} {1 - p(s + 2)}y(s + 1) = \frac{1} {\left [1 - p(s + 1)\right ]\left [1 - p(s + 2)\right ]}.}$$

Proceeding in this matter we get by mathematical induction that

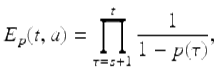
$$\displaystyle{E_{p}(t,a) =\prod _{ \tau =s+1}^{t} \frac{1} {1 - p(\tau )},}$$

for $$t \in \mathbb{N}_{s+1}$$ . By our convention on products we get

$$\displaystyle{E_{p}(s,s) =\prod _{ \tau =s+1}^{s}[1 - p(\tau )] = 1}$$

as desired. Now assume a ≤ t < s. Solving the nabla difference equation (3.5) for y(t − 1) we obtain

$$\displaystyle\begin{array}{rcl} y(t - 1) = [1 - p(t)]y(t),\quad t \in \mathbb{N}_{a+1}.& &{}\end{array}$$

(3.9)

Letting t = s in (3.9) we get

$$\displaystyle{y(s - 1) = [1 - p(s)]y(s) = [1 - p(s)].}$$

If s − 2 ≥ a, we obtain by letting $$t = s - 1$$ in (3.9)

$$\displaystyle{y(s - 2) = [1 - p(s - 1)]y(s - 1) = \left [1 - p(s)\right ]\left [1 - p(s - 1)\right ].}$$

By mathematical induction we arrive at

$$\displaystyle{E_{p}(t,s) =\prod _{ \tau =t+1}^{s}[1 - p(\tau )],\quad \mbox{ for}\quad t \in \mathbb{N}_{ a}^{s}.}$$

Hence, E p (t, s) is given by (3.7). □ 

Theorem 3.6 gives us the following example.

Example 3.7.

If $$s \in \mathbb{N}_{a}$$ and p(t) ≡ p 0, where p 0 ≠ 1 is a constant, then

$$\displaystyle{E_{p}(t,s) = (1 - p_{0})^{s-t},\quad t \in \mathbb{N}_{ a}.}$$

We now set out to prove properties of the exponential function E p (t, s). To motivate some of these properties, consider, for $$p,q \in \mathcal{R}$$ , the product

$$\displaystyle\begin{array}{rcl} & & E_{p}(t,a)E_{q}(t,a) =\prod _{ \tau =a+1}^{t} \frac{1} {1 - p(\tau )}\prod _{\tau =a+1}^{t} \frac{1} {1 - q(\tau )} {}\\ & & \quad \quad \quad =\prod _{ \tau =a+1}^{t} \frac{1} {\left [1 - p(\tau )\right ]\left [1 - q(\tau )\right ]} {}\\ & & \quad \quad \quad =\prod _{ \tau =a+1}^{t} \frac{1} {1 -\left [p(\tau ) + q(\tau ) - p(\tau )q(\tau )\right ]} {}\\ & & \quad \quad \quad =\prod _{ \tau =a+1}^{t} \frac{1} {1 - (p \boxplus q)(\tau )}\quad \mbox{ if $(p \boxplus q)(t):= p(t) + q(t) - p(t)q(t)$} {}\\ & & \quad \quad \quad = E_{p\boxplus q}(t,a) {}\\ \end{array}$$

for $$t \in \mathbb{N}_{a}$$ .

Hence, we deduce that the nabla exponential function satisfies the law of exponents

$$\displaystyle{E_{p}(t,a)E_{q}(t,a) = E_{p\boxplus q}(t,a),\quad t \in \mathbb{N}_{a},}$$

if we define the box plus addition $$\boxplus $$ on $$\mathcal{R}$$ by

$$\displaystyle{(p \boxplus q)(t):= p(t) + q(t) - p(t)q(t),\quad t \in \mathbb{N}_{a+1}.}$$

We now give an important result concerning the box plus addition $$\boxplus $$ .

Theorem 3.8.

If we define the box plus addition, $$\boxplus $$ , on $$\mathcal{R}$$ by

$$\displaystyle{p \boxplus q:= p + q - pq,}$$

then $$\mathcal{R}$$ , $$\boxplus $$ is an Abelian group.

Proof.

First, to see that the closure property is satisfied, note that if $$p,q \in \mathcal{R}$$ , then 1 − p(t) ≠ 0 and 1 − q(t) ≠ 0 for $$t \in \mathbb{N}_{a+1}$$ . It follows that

$$\displaystyle{ 1 - (p \boxplus q)(t) = 1 -\left [p(t) + q(t) - p(t)q(t)\right ] = (1 - p(t))(1 - q(t))\neq 0, }$$

for $$t \in \mathbb{N}_{a+1}$$ , and hence the function $$p \boxplus q \in \mathcal{R}$$ .

Next, notice that the zero function, 0, is in $$\mathcal{R}$$ , since the regressivity condition $$1 - 0 = 1\neq 0$$ holds. Also

$$\displaystyle{0 \boxplus p = 0 + p - 0 \cdot p = p,\quad \mbox{ for all $p \in \mathcal{R}$},}$$

so the zero function 0 is the identity element in $$\mathcal{R}$$ .

We now show that every element in $$\mathcal{R}$$ has an additive inverse let $$p \in \mathcal{R}$$ . So, set $$q = \frac{-p} {1-p}$$ and note that since

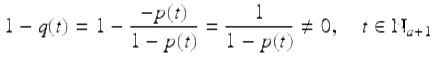
$$\displaystyle{1 - q(t) = 1 - \frac{-p(t)} {1 - p(t)} = \frac{1} {1 - p(t)}\neq 0,\quad t \in \mathbb{N}_{a+1}}$$

we have that $$q \in \mathcal{R},$$ and we also have that

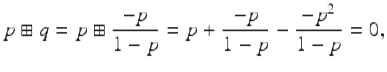
$$\displaystyle{p \boxplus q = p \boxplus \frac{-p} {1 - p} = p + \frac{-p} {1 - p} - \frac{-p^{2}} {1 - p} = 0,}$$

so q is the additive inverse of p. For $$p \in \mathcal{R},$$ we use the following notation for the additive inverse of p:

$$\displaystyle{ \boxminus p:= \frac{-p} {1 - p}. }$$

(3.10)

The fact that the addition $$\boxplus $$ is associative and commutative is Exercise 3.4. □ 

We can now define box minus subtraction, $$\boxminus,$$ on $$\mathcal{R}$$ in a standard manner as follows.

Definition 3.9.

We define box minus subtraction on $$\mathcal{R}$$ by

$$\displaystyle{p \boxminus q:= p \boxplus [\boxminus q].}$$

By Exercise 3.5 we have that if $$p,q \in \mathcal{R}$$ , then

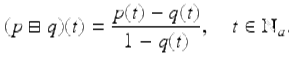
$$\displaystyle{(p \boxminus q)(t) = \frac{p(t) - q(t)} {1 - q(t)},\quad t \in \mathbb{N}_{a}.}$$

In addition, we define the set of (nabla) positively regressive functions, $$\mathcal{R}^{+},$$ by

$$\displaystyle{\mathcal{R}^{+} =\{ p: \mathbb{N}_{ a+1}:\rightarrow \mathbb{R},\quad \mbox{ such that}\quad 1 - p(t) > 0\quad \mbox{ for}\quad t \in \mathbb{N}_{a+1}\}.}$$

The proof of the following theorem is left as an exercise (see Exercise 3.8).

Theorem 3.10.

The set of positively regressive functions, $$\mathcal{R}^{+}$$ , with the addition $$\boxplus $$ , is a subgroup of $$\mathcal{R}$$ .

In the next theorem we give several properties of the exponential function E p (t, s).

Theorem 3.11.

Assume $$p,q \in \mathcal{R}$$ and $$s,r \in \mathbb{N}_{a}$$ . Then

(i)

E 0 (t,s) = 1, $$t \in \mathbb{N}_{a};$$

(ii)

E p (t,s) ≠ 0, $$t \in \mathbb{N}_{a};$$

(iii)

if $$p \in \mathcal{R}^{+}$$ , then E p (t,s) > 0, $$t \in \mathbb{N}_{a};$$

(iv)

∇E p (t,s) = p(t)E p (t,s), $$t \in \mathbb{N}_{a+1},$$ and E p (t,t) = 1, $$t \in \mathbb{N}_{a};$$

(v)

$$E_{p}(\rho (t),s) = [1 - p(t)]E_{p}(t,s)$$ , $$t \in \mathbb{N}_{a+1};$$

(vi)

E p (t,s)E p (s,r) = E p (t,r), $$t \in \mathbb{N}_{a};$$

(vii)

$$E_{p}(t,s)E_{q}(t,s) = E_{p\boxplus q}(t,s),$$ $$t \in \mathbb{N}_{a};$$

(viii)

$$E_{\boxminus p}(t,s) = \frac{1} {E_{p}(t,s)},$$ $$t \in \mathbb{N}_{a};$$

(ix)

$$\frac{E_{p}(t,s)} {E_{q}(t,s)} = E_{p\boxminus q}(t,s),$$ $$t \in \mathbb{N}_{a}$$ .

Proof.

Using Example 3.7, we have that

$$\displaystyle{E_{0}(t,s) = (1 - 0)^{s-t} = 1}$$

and thus (i) holds.

To see that (ii) holds, note that since $$p \in \mathcal{R}$$ , it follows that 1 − p(t) ≠ 0, and hence we have that for $$t \in \mathbb{N}_{s}$$

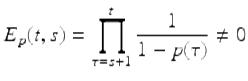
$$\displaystyle{E_{p}(t,s) =\prod _{ \tau =s+1}^{t} \frac{1} {1 - p(\tau )}\neq 0}$$

and for $$t \in \mathbb{N}_{a}^{s-1}$$

$$\displaystyle{E_{p}(t,s) =\prod _{ \tau =t+1}^{s}[1 - p(\tau )]\neq 0.}$$

Hence, (ii) holds. The proof of (iii) is similar to the proof of (ii), whereas property (iv) follows from the definition of E p (t, s).

Since, for $$t \in \mathbb{N}_{s},$$

$$\displaystyle\begin{array}{rcl} E_{p}(\rho (t),s)& =& \prod _{\tau =s+1}^{t-1} \frac{1} {1 - p(\tau )} {}\\ & =& [1 - p(t)]\prod _{\tau =s+1}^{t} \frac{1} {1 - p(\tau )} {}\\ & =& [1 - p(t)]E_{p}(t,s) {}\\ \end{array}$$

we have that (v) holds for $$t \in \mathbb{N}_{s+1}$$ . Next assume $$t \in \mathbb{N}_{a+1}^{s-1}$$ . Then

$$\displaystyle\begin{array}{rcl} E_{p}(\rho (t),s)& =& \prod _{\tau =\rho (t)+1}^{s}\left [1 - p(\tau )\right ] {}\\ & =& \prod _{\tau =t}^{s}\left [1 - p(\tau )\right ] {}\\ & =& [1 - p(t)]\prod _{\tau =t+1}^{s}\left [1 - p(\tau )\right ] {}\\ & =& [1 - p(t)]E_{p}(t,s). {}\\ \end{array}$$

Hence, (v) holds for $$t \in \mathbb{N}_{a+1}^{s-1}$$ . It is easy to check that $$E_{p}(\rho (s),s) = \left [1 - p(s)\right ]E_{p}(s,s)$$ . This completes the proof of (v).

We will just show that (vi) holds when s ≥ r ≥ a. First consider the case $$t \in \mathbb{N}_{s}$$ . In this case

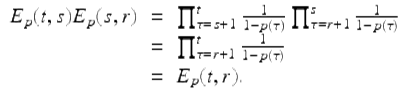
$$\displaystyle\begin{array}{rcl} E_{p}(t,s)E_{p}(s,r)& =& \prod _{\tau =s+1}^{t} \frac{1} {1 - p(\tau )}\prod _{\tau =r+1}^{s} \frac{1} {1 - p(\tau )} {}\\ & =& \prod _{\tau =r+1}^{t} \frac{1} {1 - p(\tau )} {}\\ & =& E_{p}(t,r). {}\\ \end{array}$$

Next, consider the case $$t \in \mathbb{N}_{r}^{s-1}$$ . Then

$$\displaystyle\begin{array}{rcl} E_{p}(t,s)E_{p}(s,r)& =& \prod _{\tau =t+1}^{s}\left [1 - p(\tau )\right ]\prod _{\tau =r+1}^{s} \frac{1} {1 - p(\tau )} {}\\ & =& \prod _{\tau =r+1}^{t} \frac{1} {1 - p(\tau )} {}\\ & =& E_{p}(t,r). {}\\ \end{array}$$

Finally, consider the case $$t \in \mathbb{N}_{a}^{r-1}$$ . Then

$$\displaystyle\begin{array}{rcl} E_{p}(t,s)E_{p}(s,r)& =& \prod _{\tau =t+1}^{s}\left [1 - p(\tau )\right ]\prod _{\tau =r+1}^{s} \frac{1} {1 - p(\tau )} {}\\ & =& \prod _{\tau =r+1}^{t}\left [1 - p(\tau )\right ] {}\\ & =& E_{p}(t,r). {}\\ \end{array}$$

This completes the proof of (vi) for the special case s ≥ r ≥ a. The case a ≤ s ≤ r is left to the reader (Exercise 3.9). The proof of the law of exponents (vii) is Exercise 3.10. To see that (viii) holds, note that for $$t \in \mathbb{N}_{s}$$

$$\displaystyle\begin{array}{rcl} E_{\boxminus p}(t,s)& =& \prod _{\tau =s+1}^{t} \frac{1} {1 - (\boxminus p)(\tau )} {}\\ & =& \prod _{\tau =s+1}^{t}\left [1 - p(\tau )\right ] {}\\ & =& \frac{1} {E_{p}(t,s)}. {}\\ \end{array}$$

Also, if $$t \in \mathbb{N}_{a}^{s-1}$$

$$\displaystyle\begin{array}{rcl} E_{\boxminus p}(t,s)& =& \prod _{\tau =t+1}^{s}\left [1 - (\boxminus p)(\tau )\right ] {}\\ & =& \prod _{\tau =t+1}^{s} \frac{1} {1 - p(\tau )} {}\\ & =& \frac{1} {E_{p}(t,s)}. {}\\ \end{array}$$

Hence (viii) holds for $$t \in \mathbb{N}_{a}$$ . Finally, using (viii) and then (vii), we have that

$$\displaystyle{ \frac{E_{p}(t,s)} {E_{q}(t,s)} = E_{p}(t,s)E_{\boxminus q}(t,s) = E_{p\boxplus [\boxminus q]}(t,s) = E_{p\boxminus q}(t,s), }$$

from which it follows that (ix) holds. □ 

Next we define the scalar box dot multiplication, $$\boxdot $$ .

Definition 3.12.

For $$\alpha \in \mathbb{R},$$ $$p \in \mathcal{R}^{+}$$ the scalar box dot multiplication, $$\alpha \boxdot p$$ , is defined by

$$\displaystyle{\alpha \boxdot p = 1 - (1 - p)^{\alpha }.}$$

It follows that for $$\alpha \in \mathbb{R},$$ $$p \in \mathcal{R}^{+}$$

$$\displaystyle\begin{array}{rcl} 1 - (\alpha \boxdot p)(t)& =& 1 -\left \{1 -\left [1 - p(t)\right ]^{\alpha }\right \} {}\\ & =& \left [1 - p(t)\right ]^{\alpha } > 0 {}\\ \end{array}$$

for $$t \in \mathbb{N}_{a+1}$$ . Hence $$\alpha \boxdot p \in \mathcal{R}^{+}$$ .

Now we can prove the following law of exponents.

Theorem 3.13.

If $$\alpha \in \mathbb{R}$$ and $$p \in \mathcal{R}^{+}$$ , then

$$\displaystyle{E_{p}^{\alpha }(t,a) = E_{\alpha \boxdot p}(t,a)}$$

for $$t \in \mathbb{N}_{a}$$ .

Proof.

Consider that, for $$t \in \mathbb{N}_{a}$$ ,

$$\displaystyle\begin{array}{rcl} E_{p}^{\alpha }(t,a)& =& \left [\prod _{\tau =a+1}^{t} \frac{1} {1 + p(\tau )}\right ]^{\alpha } {}\\ & =& \prod _{\tau =a+1}^{t} \frac{1} {[1 + p(\tau )]^{\alpha }} {}\\ & =& \prod _{\tau =a+1}^{t} \frac{1} {1 - [1 - (1 - p(\tau ))^{\alpha }]} {}\\ & =& \prod _{\tau =a+1}^{t} \frac{1} {1 - [\alpha \boxdot p](\tau )} {}\\ & =& E_{\alpha \boxdot p}(t,a). {}\\ \end{array}$$

This completes the proof. □ 

Theorem 3.14.

The set of positively regressive functions $$\mathcal{R}^{+}$$ , with the addition $$\boxplus $$ and the scalar multiplication $$\boxdot $$ , is a vector space.

Proof.

From Theorem 3.10 we know that $$\mathcal{R}^{+}$$ with the addition $$\boxplus $$ is an Abelian group. The four remaining nontrivial properties of a vector space are the following:

(i)

$$1 \boxdot p = p;$$

(ii)

$$\alpha \boxdot (p \boxplus q) = (\alpha \boxdot p) \boxplus (\alpha \boxdot q);$$

(iii)

$$\alpha \boxdot (\beta \boxdot p) = (\alpha \beta ) \boxdot p;$$

(iv)

$$(\alpha +\beta ) \boxdot p = (\alpha \boxdot p) \boxplus (\beta \boxdot p),$$

where $$\alpha,\beta \in \mathbb{R}$$ and $$p,q \in \mathcal{R}^{+}$$ . We will prove properties (i)–(iii) and leave property (iv) as an exercise (Exercise 3.12).

Property (i) follows immediately from the following:

$$\displaystyle{1 \boxdot p = 1 - (1 - p)^{1} = p.}$$

To prove (ii) consider

$$\displaystyle\begin{array}{rcl} & & (\alpha \boxdot p) \boxplus (\alpha \boxdot q) {}\\ & & \qquad \qquad =\alpha \boxdot p +\alpha \boxdot q - (\alpha \boxdot p)(\alpha \boxdot q) {}\\ & & \qquad \qquad = [1 - (1 - p)^{\alpha }] + [1 - (1 - q)^{\alpha }] - [1 - (1 - p)^{\alpha }][1 - (1 - q)^{\alpha }] {}\\ & & \qquad \qquad = 1 - (1 - p)^{\alpha }(1 - q)^{\alpha } {}\\ & & \qquad \qquad = 1 - (1 - p - q + pq)^{\alpha } {}\\ & & \qquad \qquad = 1 - (1 - p \boxplus q)^{\alpha } {}\\ & & \qquad \qquad =\alpha \boxdot (p \boxplus q). {}\\ \end{array}$$

Hence, (ii) holds. Finally, consider

$$\displaystyle\begin{array}{rcl} \alpha \boxdot (\beta \boxplus p)& =& 1 - (1 -\beta \boxdot p)^{\alpha } {}\\ & =& 1 -\bigg [1 -\left [1 - (1 - p)^{\beta }\right ]\bigg]^{\alpha } {}\\ & =& 1 - (1 - p)^{\alpha \beta } {}\\ & =& (\alpha \beta ) \boxdot p. {}\\ \end{array}$$

Hence, property (iii) holds. □