Nabla Laplace Transforms - Nabla Fractional Calculus - Discrete Fractional Calculus

Discrete Fractional Calculus (2015)

3. Nabla Fractional Calculus

3.10. Nabla Laplace Transforms

Having established the necessary preliminaries, we are now ready to discuss an important application of this material: the Laplace transform. The Laplace transform, as in the standard calculus, will provide us with an elegant way to solve initial value problems for a fractional nabla difference equation. In this section, we will lay the groundwork for this method, prove the basic properties, and establish a means in which to solve various initial value (nabla) fractional difference equations. We begin this section by defining the nabla Laplace transform operator $$\mathcal{L}_{a}$$ (based at a) as follows:

Definition 3.64.

Assume $$f: \mathbb{N}_{a+1} \rightarrow \mathbb{R}$$ . Then the nabla Laplace transform of f is defined by

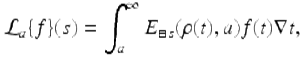
$$\displaystyle{\mathcal{L}_{a}\{f\}(s) =\int _{ a}^{\infty }E_{ \boxminus s}(\rho (t),a)f(t)\nabla t,}$$

for those values of s ≠ 1 such that this improper integral converges.

In the following theorem we give another formula for the Laplace transform, which is often more convenient to use.

Theorem 3.65.

Assume $$f: \mathbb{N}_{a+1} \rightarrow \mathbb{R}$$ . Then

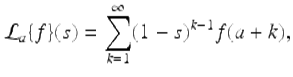
$$\displaystyle{ \mathcal{L}_{a}\{f\}(s) =\sum _{ k=1}^{\infty }(1 - s)^{k-1}f(a + k), }$$

(3.36)

for those values of s such that this infinite series converges.

Proof.

Assume $$f: \mathbb{N}_{a+1} \rightarrow \mathbb{R}$$ . Then

$$\displaystyle\begin{array}{rcl} \mathcal{L}_{a}\{f\}(s)& =& \int _{a}^{\infty }E_{ \boxminus s}(\rho (t),a)f(t)\nabla t {}\\ & =& \int _{a}^{\infty }[1 -\boxminus s]^{a-t+1}f(t)\nabla t {}\\ & =& \int _{a}^{\infty }\left ( \frac{1} {1 - s}\right )^{a-t+1}f(t)\nabla t {}\\ & =& \int _{a}^{\infty }(1 - s)^{t-a-1}f(t)\nabla t {}\\ & =& \sum _{t=a+1}^{\infty }(1 - s)^{t-a-1}f(t) {}\\ & =& \sum _{k=1}^{\infty }(1 - s)^{k-1}f(a + k), {}\\ \end{array}$$

for those values of s such that this infinite series converges. □ 

In the definition of the nabla Laplace transform we assumed s ≠ 1 because we do not define $$E_{\boxminus 1}(t,a)$$ . But the formula of the nabla Laplace transform (3.36) is well defined when s = 1. From now on we will always include s = 1 in the domain of convergence for the nabla Laplace transform although in the proofs we will often assume s ≠ 1. In fact the formula (3.36) for any $$f: \mathbb{N}_{a+1} \rightarrow \mathbb{R}$$ gives us that

$$\displaystyle{\mathcal{L}_{a}\{f\}(1) = f(a + 1).}$$

Example 3.66.

We use the last theorem to find $$\mathcal{L}_{a}\{1\}(s)$$ . By Theorem 3.65 we obtain

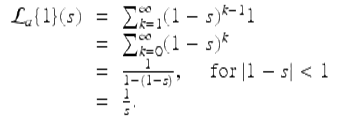
$$\displaystyle\begin{array}{rcl} \mathcal{L}_{a}\{1\}(s)& =& \sum _{k=1}^{\infty }(1 - s)^{k-1}1 {}\\ & =& \sum _{k=0}^{\infty }(1 - s)^{k} {}\\ & =& \frac{1} {1 - (1 - s)},\quad \mbox{ for $\vert 1 - s\vert < 1$} {}\\ & =& \frac{1} {s}. {}\\ \end{array}$$

That is

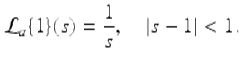
$$\displaystyle{\mathcal{L}_{a}\{1\}(s) = \frac{1} {s},\quad \vert s - 1\vert < 1.}$$

Theorem 3.67.

For all nonnegative integers n, we have that

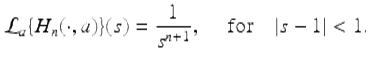
$$\displaystyle{\mathcal{L}_{a}\{H_{n}(\cdot,a)\}(s) = \frac{1} {s^{n+1}},\quad \mbox{ for}\quad \vert s - 1\vert < 1.}$$

Proof.

The proof is by induction on n. The result is true for n = 0 by the previous example. Suppose now that $$\mathcal{L}_{a}\{H_{n}(\cdot,a)\}(s) = \frac{1} {s^{n+1}}$$ for some fixed n ≥ 0 and | s − 1 |  < 1. Then consider

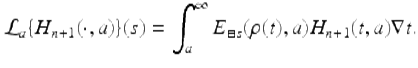
$$\displaystyle{\mathcal{L}_{a}\{H_{n+1}(\cdot,a)\}(s) =\int _{ a}^{\infty }E_{ \boxminus s}(\rho (t),a)H_{n+1}(t,a)\nabla t.}$$

We will apply the first integration by parts formula (3.19) with

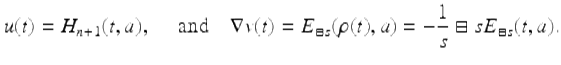
$$\displaystyle{u(t) = H_{n+1}(t,a),\quad \mbox{ and}\quad \nabla v(t) = E_{\boxminus s}(\rho (t),a) = -\frac{1} {s} \boxminus sE_{\boxminus s}(t,a).}$$

It follows that

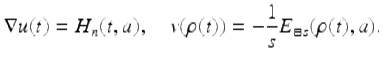
$$\displaystyle{\nabla u(t) = H_{n}(t,a),\quad v(\rho (t)) = -\frac{1} {s}E_{\boxminus s}(\rho (t),a).}$$

Hence by the integration by parts formula (3.19)

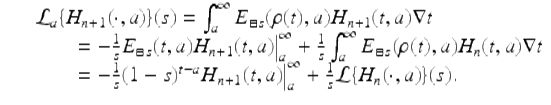
$$\displaystyle\begin{array}{rcl} & & \mathcal{L}_{a}\{H_{n+1}(\cdot,a)\}(s) =\int _{ a}^{\infty }E_{ \boxminus s}(\rho (t),a)H_{n+1}(t,a)\nabla t {}\\ & & \quad \quad = -\frac{1} {s}E_{\boxminus s}(t,a)H_{n+1}(t,a)\big\vert _{a}^{\infty } + \frac{1} {s}\int _{a}^{\infty }E_{ \boxminus s}(\rho (t),a)H_{n}(t,a)\nabla t {}\\ & & \quad \quad = -\frac{1} {s}(1 - s)^{t-a}H_{ n+1}(t,a)\big\vert _{a}^{\infty } + \frac{1} {s}\mathcal{L}\{H_{n}(\cdot,a)\}(s). {}\\ \end{array}$$

Using the nabla form of L’Hôpital’s rule (Exercise 3.19) we calculate

$$\displaystyle\begin{array}{rcl} \lim _{t\rightarrow \infty }\vert (1 - s)^{t-a}H_{ n+1}(t,a)\vert & =& \lim _{t\rightarrow \infty }\frac{H_{n+1}(t,a)} {\vert 1 - s\vert ^{a-t}} {}\\ & =& \lim _{t\rightarrow \infty } \frac{H_{n}(t,a)} {[1 -\vert 1 - s\vert ]\vert 1 - s\vert ^{a-t}} {}\\ & =& \lim _{t\rightarrow \infty } \frac{H_{n-1}(t,a)} {[1 -\vert 1 - s\vert ]^{2}\vert 1 - s\vert ^{a-t}} {}\\ & =& \cdots {}\\ & =& \lim _{t\rightarrow \infty } \frac{H_{0}(t,a)} {[1 -\vert 1 - s\vert ]^{n+1}\vert 1 - s\vert ^{a-t}} {}\\ & =& 0, {}\\ \end{array}$$

since | s − 1 |  < 1. Thus we have that

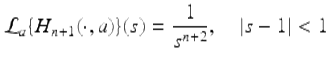
$$\displaystyle{\mathcal{L}_{a}\{H_{n+1}(\cdot,a)\}(s) = \frac{1} {s^{n+2}},\quad \vert s - 1\vert < 1}$$

completing the proof. □ 

Definition 3.68.

A function $$f: \mathbb{N}_{a+1} \rightarrow \mathbb{R}$$ is said to be of exponential order r > 0 if there exist a constant M > 0 and a number $$T \in \mathbb{N}_{a+1}$$ such that

$$\displaystyle{\vert f(t)\vert \leq Mr^{t},\quad \mbox{ for all $t \in \mathbb{N}_{ T}$}.}$$

Theorem 3.69.

For $$n \in \mathbb{N}_{1}$$ , the Taylor monomials H n (t,a) are of exponential order 1 + ε for all ε > 0. Also, H 0 (t,a) is of exponential order 1.

Proof.

Since

$$\displaystyle{\vert H_{0}(t,a)\vert = 1 \cdot 1^{t},\quad t \in \mathbb{N}_{ a+1},}$$

H 0(t, a) is of exponential order 1. Next, assume $$n \in \mathbb{N}_{1}$$ and ε > 0 is fixed. Using repeated applications of the nabla L’Hôpital’s rule, we get

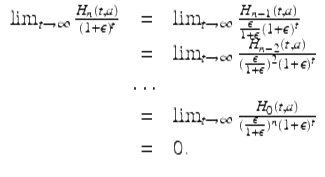
$$\displaystyle\begin{array}{rcl} \lim _{t\rightarrow \infty }\frac{H_{n}(t,a)} {(1+\epsilon )^{t}} & =& \lim _{t\rightarrow \infty }\frac{H_{n-1}(t,a)} { \frac{\epsilon }{1+\epsilon }(1+\epsilon )^{t}} {}\\ & =& \lim _{t\rightarrow \infty }\frac{H_{n-2}(t,a)} {( \frac{\epsilon }{1+\epsilon })^{2}(1+\epsilon )^{t}} {}\\ & \cdots & {}\\ & =& \lim _{t\rightarrow \infty } \frac{H_{0}(t,a)} {( \frac{\epsilon }{1+\epsilon })^{n}(1+\epsilon )^{t}} {}\\ & =& 0. {}\\ \end{array}$$

It follows from this that each H n (t, a), $$n \in \mathbb{N}_{1}$$ , is of exponential order 1 +ε for all ε > 0. □ 

Theorem 3.70 (Existence of Nabla Laplace Transform).

If $$f: \mathbb{N}_{a+1} \rightarrow \mathbb{R}$$ is a function of exponential order r > 0, then its Laplace transform exists for $$\vert s - 1\vert < \frac{1} {r}$$ .

Proof.

Let f be a function of exponential order r. Then there is a constant M > 0 and a number $$T \in \mathbb{N}_{a+1}$$ such that | f(t) | ≤ Mr t for all $$t \in \mathbb{N}_{T}$$ . Pick K so that $$T = a + K$$ , then we have that

$$\displaystyle{\vert f(a + k)\vert \leq Mr^{a+k},\quad k \in \mathbb{N}_{ K}.}$$

We now show that

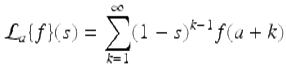
$$\displaystyle{\mathcal{L}_{a}\{f\}(s) =\sum _{ k=1}^{\infty }(1 - s)^{k-1}f(a + k)}$$

converges for $$\vert s - 1\vert < \frac{1} {r}$$ . To see this, consider

$$\displaystyle\begin{array}{rcl} \sum _{k=K}^{\infty }\vert (1 - s)^{k-1}f(a + k)\vert & =& \sum _{ k=K}^{\infty }\vert 1 - s\vert ^{k-1}\vert f(a + k)\vert {}\\ &\leq & \sum _{k=K}^{\infty }\vert 1 - s\vert ^{k-1}Mr^{a+k} {}\\ & =& Mr^{a+1}\sum _{ k=K}^{\infty }[r\vert s - 1\vert ]^{k-1}, {}\\ \end{array}$$

which converges since r | s − 1 |  < 1. It follows that $$\mathcal{L}_{a}\{f\}(s)$$ converges absolutely for $$\vert s - 1\vert < \frac{1} {r}$$ . □ 

Theorem 3.71.

The Laplace transform of the Taylor monomial, H n (t,a), $$n \in \mathbb{N}_{0}$$ , exists for |s − 1| < 1.

Proof.

The proof of this theorem follows from Theorems 3.69 and 3.70. □ 

Similarly, by Exercise 3.30 each of the functions E p (t, a), Cosh p (t, a), Sinh p (t, a), Cos p (t, a), and Sin p (t, a) is of exponential order | 1 + p | , and hence by Theorem 3.70 their Laplace transforms exist for $$\vert s - 1\vert < \frac{1} {\vert 1+p\vert }$$ .

Theorem 3.72 (Uniqueness Theorem).

Assume $$f,g: \mathbb{N}_{a+1} \rightarrow \mathbb{R}$$ . Then f(t) = g(t), $$t \in \mathbb{N}_{a+1},$$ if and only if

$$\displaystyle{\mathcal{L}_{a}\{f\}(s) = \mathcal{L}_{a}\{g\}(s),\quad \mbox{ for}\quad \vert s - 1\vert < r}$$

for some r > 0.

Proof.

Since $$\mathcal{L}_{a}$$ is a linear operator it suffices to show that f(t) = 0 for $$t \in \mathbb{N}_{a+1}$$ if and only if $$\mathcal{L}_{a}\{f\}(s) = 0$$ for | s − 1 |  < r for some r > 0. If f(t) = 0 for $$t \in \mathbb{N}_{a+1}$$ , then trivially $$\mathcal{L}_{a}\{f\}(s) = 0$$ for all $$s \in \mathbb{C}$$ . Conversely, assume that $$\mathcal{L}_{a}\{f\}(s) = 0$$ for | s − 1 |  < r for some r > 0. In this case we have that

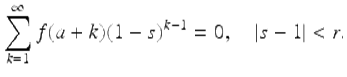
$$\displaystyle{\sum _{k=1}^{\infty }f(a + k)(1 - s)^{k-1} = 0,\quad \vert s - 1\vert < r.}$$

This implies that

$$\displaystyle{f(t) = 0,\quad t \in \mathbb{N}_{a+1}.}$$

This completes the proof. □